Физическая сторона задачи

Запишем закон Гука, связывающий касательные напряжения с углом сдвига

 = G . (7.5)

Математическая сторона задачи

Подставим выражение (7.4) в формулу (7.5):

 = G ⋅, 7.6)

а полученное выражение (7.6) – в формулу (7.3):

Mz = (7.7)

Так как в выражении (7.7) величины G и d/dz в соответствии с принятыми гипотезами, остаются постоянными по данному сечению, то их можно вынести за знак интеграла:

Mz =

Величина

J_p =

называется полярным моментом инерции и является геометрической характеристикой данного сечения.

Таким образом, окончательно можем записать

Mz = J_p (7.8)

или, подставляя (7.6) в (7.8),

Mz = .

Величина касательных напряжений при кручении определяется следующим образом:

 =

К ак видим, касательные напряжения распределены по сечению вала по линейному закону и достигают максимальной величины на поверхности вала (при ρ=ρmax):

_max = = ,

где Wp = Jp/max – полярный момент сопротивления.

Из формулы (7.8) легко найти и другие величины, характеризующие деформацию вала при кручении.

Величина

(7.9)

называется относительным (погонным) углом закручивания и имеет размерность рад/м.

Используя выражение (7.8), найдем формулу для определения относительного угла закручивания:

. (7.10)

Зная формулы (7.9) и7.10) для определения относительного угла закручивания, можно записать формулу для определения взаимного угла поворота двух сечений, расположенных на расстоянии l друг от друга:

Если в пределах участка длиной l крутящий момент и геометрические характеристики сечения вала остаются постоянными, то угол закручивания можно определить как ⋅

 = l =

7.3. Напряженное состояние и виды разрушения при кручении

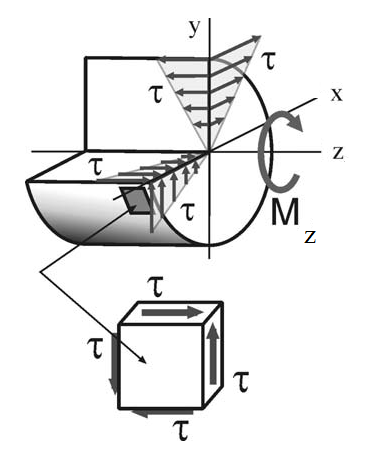
Исследуем напряженное состояние при кручении. По закону парности касательных напряжений в диаметральных сечениях вала возникают такие же касательные напряжения, как и в поперечном сечении. При этом все остальные напряжения равны нулю, то есть при кручении возникает частный случай плоского напряженного состояния – чистый сдвиг.

К ак было показано ранее, главные нормальные напряжения σ₁ и σ₃ при чистом сдвиге противоположны по знаку, одинаковы по величине и в наиболее опасных точках (на поверхности вала) равны τ_max:

σ₁ = τ_max , . σ₃ = -τ_max

Кроме того известно, что главные напряжения при чистом сдвиге действуют по линии (для цилиндрического образца – по винтовой линии), наклоненной к оси вала под углом 45^о.

Именно по этой линии, как показывают эксперименты, будут разрушаться хрупкие материалы (например, чугун), которые плохо сопротивляются растягивающим напряжениям. Материалы, плохо сопротивляющиеся действию касательных напряжений, будут разрушаться в плоскостях действия наибольших касательных напряжений: например, в случае кручения деревянных валов с продольным расположением волокон трещины разрушения ориентированы вдоль образующей, а стальные валы в пластическом состоянии на практике часто разрушаются по поперечному сечению, перпендикулярному к оси вала.