2013_2014 учебный год II семестр Лекция № 2.7 стр. 8

Кручение стержней круглого поперечного сечения

7.1. Определение внутренних усилий при кручении. Построение эпюр крутящих моментов

К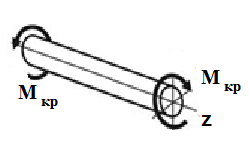 ручение – простой вид сопротивления (нагружения), при котором на стержень действуют моменты в плоскостях, перпендикулярных к продольной оси стержня.

Стержень, работающий на кручение, в дальнейшем будем называть валом.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

Пусть вал вращается с постоянной скоростью n об/мин и передает мощность N Нм/с. Угловая скорость вращения вала равна  = (рад/сек), а передаваемая мощность N = T.

Скручивающий момент равен

Если мощность задана в киловаттах, то величина скручивающего момента определяется по формуле

.

И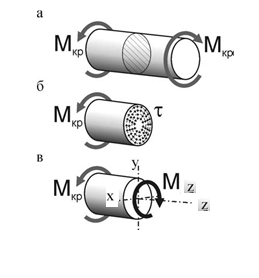 спользуя метод мысленных сечений (см. рисунок), находим величину внутренних усилий, действующих в сечении вала при кручении. Очевидно, что в данном случае нагружения из шести уравнений равновесия, составленных для отсеченной части стержня относительно внешних сил и внутренних усилий, лишь одно не обращается тождественно в ноль:

ΣM_z = 0 ⇒ M_z = M_кр.

Рис.7.1

Таким образом, при кручении в произвольном поперечном сечении вала из шести внутренних силовых факторов возникает только один – внутренний крутящий момент (М_z).

Построение эпюр крутящих моментов

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент М_к в сечении вала численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.

Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 7.2).

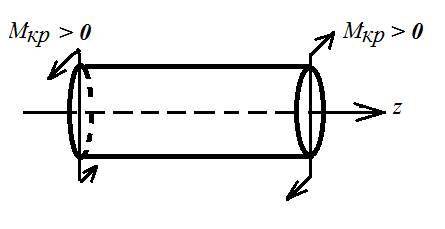
Рис.7.2

При наличии распределенной моментной нагрузки m (рис.7.3) крутящие моменты М_кр связаны дифференциальной зависимостью

dM_кр /dz =  m 7.1)

из которой вытекает следующая формула:

M_кр = M₀  mz, (7.2)

где M₀ – крутящий момент в начале участка.

h Рис.7.3

Согласно формуле (7.2) на участках с равномерно распределенной нагрузкой интенсивности m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (М_кр = М_о = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_кр возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

Пример7. 1

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.7.4, а).

Рис.7.4