Интервальные оценки
7.
Найти
доверительный интервал с надежностью
0,95 для оценки математического ожидания
нормально распределенной случайной
величины Х, если известны ее среднее
квадратическое отклонение σ = 4, выборочная
средняя
и объем
выборки n = 16.
(Ответ:
14,04 < а < 17,96).
8. Станок – автомат штампует валики. По выборке объема n = 100 вычислена выборочная средняя диаметров изготовленных валиков. Найти с надежностью 0,95 точность δ, с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их среднее квадратическое отклонение σ = 2 мм. Предполагается, что диаметры валиков распределены нормально.
(Ответ: δ =0,392 мм ).
9. В нескольких мелких магазинах проведена проверка качества 100 изделий, после чего осуществлена обработка полученных данных. В результате получено несмещенное значение выборочного среднего квадратического отклонения s = 4. Считая распределение качественных изделий нормальным, найти с надежностью γ = 0,95 доверительный интервал для оценки среднего квадратического отклонения.
(Ответ: 3,5 < σ < 4,67).
Статистические методы обработки экспериментальных данных
10.
Получить
линейную зависимость
по следующим данным
.
(Ответ:
у =
).
11.
Случайная
величина Х (число появлений события А
в m независимых испытаниях) подчинена
закону распределения Пуассона с
неизвестным параметром а:
,
где m − число испытаний в одном опыте,
- число появлений события в i-м опыте
.
Найти методом максимального правдоподобия
по выборке
точечную оценку неизвестного параметра
а распределения Пуассона.
(Ответ:
).
Проверка статистических гипотез
12.
По двум
независимым выборкам, объемы которых
и
,
извлеченным из нормальных генеральных
совокупностей Х и У, найдены исправленные
выборочные дисперсии
и
.
При уровне значимости α = 0,01 проверить
нулевую гипотезу
при конкурирующей гипотезе
.
( Fнабл
= 2,8; Fкр
= 4; нет оснований отвергнуть гипотезу
H0).
13.
По двум
независимым выборкам, объемы которых
и
,
извлеченным из нормальных генеральных
совокупностей Х и У, найдены выборочные
дисперсии
и
.
При уровне значимости 0,1 проверить
нулевую гипотезу
о
равенстве генеральных дисперсий при
конкурирующей гипотезе
.
( Fнабл
= 1,52;
Fкр
= 3,69; нет оснований отвергнуть гипотезу
H0).
14. Используя критерий Пирсона, при уровне значимости 0,05, проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объема n = 200:
.
(Ответ:
k = 8;
7,71;
15,5;
нет оснований отвергнуть гипотезу о
нормальном распределении генеральной
совокупности).
15. Используя критерий Пирсона, при уровне значимости 0,05, проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объема n = 100:
-
i
Границы интервала
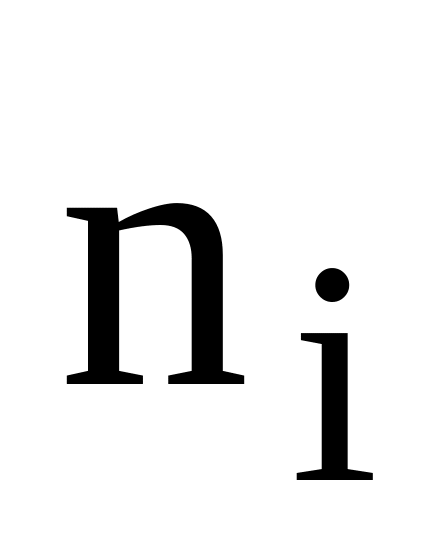
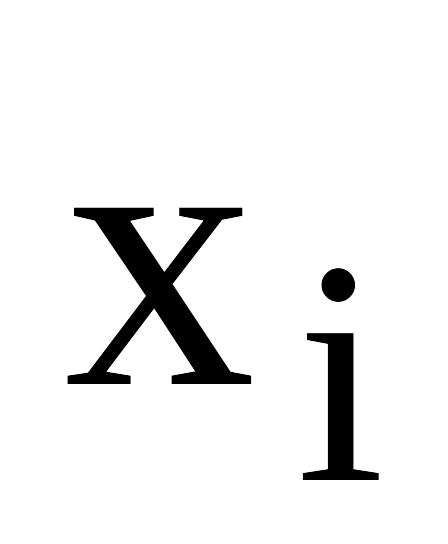
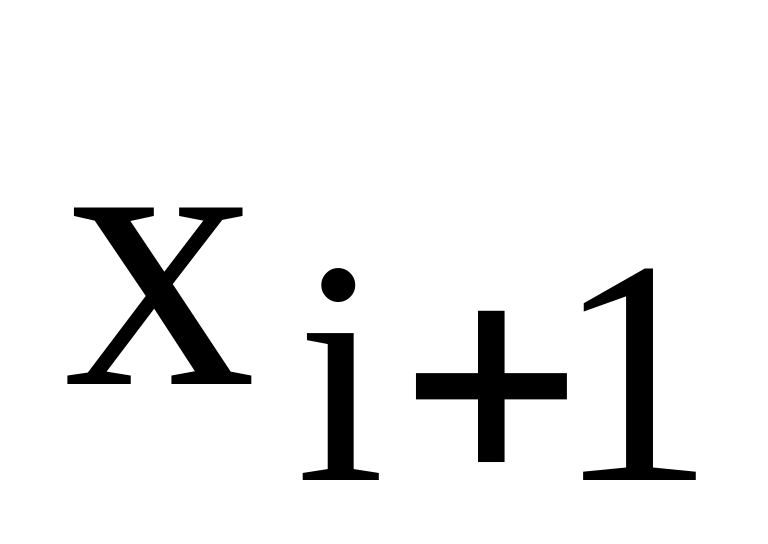
1
3
8
6
2
8
13
8
3
13
18
15
4
18
23
40
5
23
28
16
6
28
33
8
7
33
38
7
(Ответ:: k = 4; 13,22; 9,5; данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности).