1.2 Короткий опис програми рішення диференціального рівняння методом Ейлера

Для того щоб розпочати написання тексту програми розрахунку диференціального рівняння методом Ейлера, його необхідно привести до належного вигляду, тобто вирішити з урахуванням початкових умов і без них, наприклад, розглянемо рівняння виду з початковими умовами .

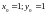Спочатку виразимо похідну:

– задана функція, наближена.

Розв’яжемо диференціальне рівняння відносно 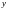проінтегрувавши його:

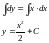
де 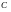– константа інтегрування, яку можна знайти підставивши початкові умови:

Рівняння тоді прийме вигляд:

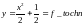
Приблизна структура програми рішення диференціального рівняння методом Ейлера:

1. Назва програми;

2. Опис змінних: ;

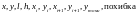3. Опис функцій та :

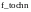function <ім’я> (список формальних параметрів: тип):тип;

begin

вираз для обчислення функції;

end;

4. Основний текст програми обмежений операторними дужками:

• відкриття і перезапис файлу з розширенням «.glo»;

• ввід відрізку і кроку інтегрування функції;

• ввід початкових умов;

• запис у файл початкових умов;

• використання оператору повторення для обчислення значень функції;

• запис похибки обчислень.

5. Запис результатів обчислень у файл з виводом на екран;

6. Закриття файлу;

7. Кінець програми.

За даних початкових умовах за допомогою розробленої програми проводимо розрахунок, а результати заносимо в таблицю.

x	y	y_toch	error

За одержаними результатами будуємо графік функції і .

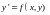1.3 Опис методу Рунге-Кутта

Метод Рунге-Кутта часто застосовується для вирішення диференціальних рівнянь і систем рівнянь із-за його високої точності.

Відмітна особливість методу – уточнення нахилу інтегральної кривої за рахунок обчислення похідної не тільки на початку поточного відрізка інтегрування, а й, наприклад, в середині відрізка або чотириразове обчислення похідних у методі четвертого порядку. Для випадку одного рівняння двочленна ітераційна формула може мати вигляд

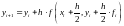
Послідовність обчислень: спочатку роблять половинний крок за схемою ламаних (по формулі Ейлера), знаходячи , потім у знайденвй точці визначають нахил кривої і з цього нахилу визначають приріст на цілому кроці .

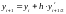Чотиричленна схема Рунге-Кутта найбільш часто вживається в машинних розрахунках і має четвертий порядок точності та описується системою з п’яти рівнянь:

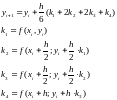
де .

Метод Рунге-Кутта потребує більшого об’єму обчислень в порівнянні з методом Ейлера, зате це компенсується підвищеною точністю.

1.4 Короткий опис програми рішення диференціального рівняння методом Рунге-Кутта

Так само як і для методу Ейлера перед написанням тексту програми розрахунку диференціального рівняння методом Рунге-Кутта, його необхідно привести до належного вигляду.

Приблизна структура програми рішення диференціального рівняння методом Рунге-Кутта майже аналогічна методу Ейлера, окрім деяких відмінностей:

1. Опис змінних: ;

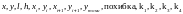2. В основному тексті програми також вводяться коефіцієнти :

За даних початкових умовах за допомогою розробленої програми проводимо розрахунок, а результати заносимо в таблицю.

x	y	y_toch	error

За одержаними результатами будуємо графік функції і .

Після проведення розрахунків звичайного диференціального рівняння двома методами робимо висновки.