Лекция 10 Вычисление определенного интеграла
1. Применение формулы Ньютона-Лейбница. Формула применяется во всех случаях, когда может быть найдена первообразная функция F(x) для подынтегральной функции f(x).
Пример.
2. Интегрирование подстановкой (замена переменной).
Теорема.
Пусть для вычисления интеграла
от непрерывной функции была сделана
подстановка х=φ(t),
причем эта функция удовлетворяет
следующим условиям: 1) функция х=φ(t)
и ее производная х’=φ’(t)
непрерывны при
;
2) отрезок
является областью определения функции
х=φ(t),
а отрезок [a;b] является областью ее
значений; 3)
.
Тогда справедлива следующая формула:
Пример.
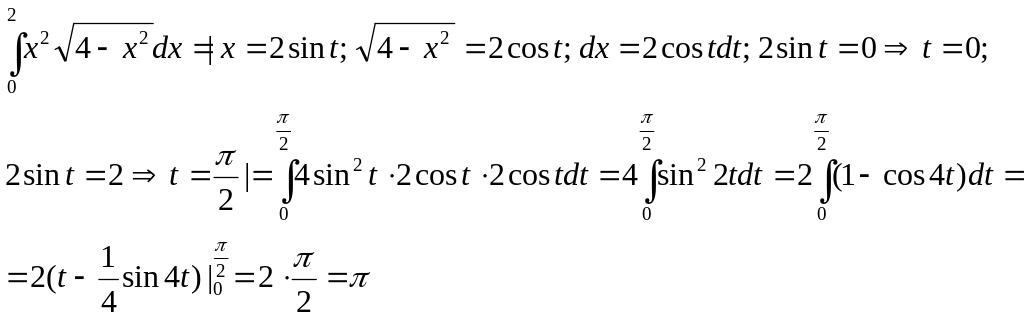
3. Интегрирование по частям.
Теорема. Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a;b], то имеет место формула:
Пример.
1)
2)
4. Интегрирование четных и нечетных функций в симметричных пределах.
Пусть задана функция непрерывная на отрезке [-a;a], симметричном относительно точки х=0. Тогда справедлива следующая формула:
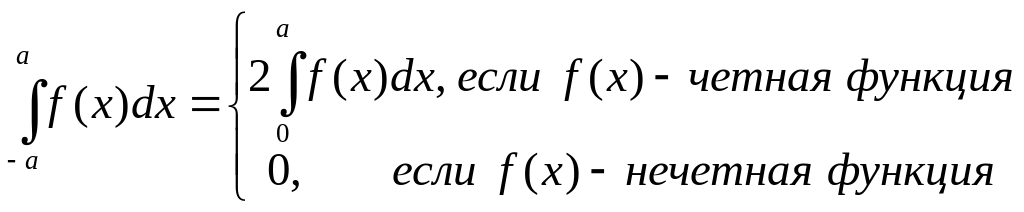
Пример.
1)
;
2)
Лекция 11 Геометрические приложения определенного интеграла
11.1. Определение площадей плоских фигур
Площадь плоской фигуры, ограниченной непрерывной кривой, уравнение которой в прямоугольных координатах имеет вид y=f(x), осью Ох и двумя прямыми х=а и х=b (a<b) находится по формуле:
Отрезок [a;b] следует разделить на части, в каждой из которых функция f(x) сохраняет один и тот же знак. При этом следует соблюдать такое правило знаков: площади, находящиеся над осью Ох, берутся со знаком плюс, а площади, расположенные под осью Ох, со знаком минус.
Если
площадь ограничена двумя непрерывными
кривыми, уравнения которых в прямоугольных
координатах
,
причем всюду на отрезке [a;b]
и двумя прямыми х=а
и х=b, то
площадь определяется по формуле:
и
в этом случае надо соблюдать указанное
правило знаков.
Примеры.
Найти площадь, ограниченную осью Ох и параболами:
1)
Решение:
Найдем
вершину параболы.
Найдем
корни параболы:
Т.к. фигура находится под осью Ох, то перед определенным интегралом ставим знак минус при определении площади фигуры:
2)
Решение:
Найдем
вершину параболы.
Найдем
корни параболы:
Т.к. фигура находится под осью Ох, то перед определенным интегралом
ставим знак минус при определении площади фигуры:
Лекция 12
Несобственные интегралы
12.1. Несобственные интегралы
с бесконечными пределами интегрирования (I рода)
Пусть
функция
интегрируема на любом отрезке
.
Тогда несобственные интегралы с
бесконечными пределами интегрирования
определяются следующим образом:
(3.1)
(3.2)
(3.3),
где с – произвольное число (обычно с=0).
Несобственные интегралы I рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях формул (3.1), (3.2), (3.3). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися.
Существуют три признака сходимости и расходимости несобственных интегралов I рода:
1.
Если на промежутке
непрерывные
функции
и
удовлетворяют
условиям
,
то из сходимости интеграла
следует сходимость интеграла
,
а из расходимости интеграла
следует расходимость интеграла
.
Этот признак называется признаком
сравнения.
2.
Если при
и существует конечный предел
,
то интегралы
и
сходятся или расходятся одновременно.
Этот признак называется предельным
признаком сравнения.
3.
Если сходится интеграл
,
то сходится и интеграл
,
который в этом случае называется
абсолютно сходящимся.
Примеры.
Выяснить, сходятся ли интегралы:
1)
2)
