8.2. Геометрический смысл определенного интеграла. Площадь криволинейной трапеции
Пусть функция определена, непрерывна и положительна на отрезке [a;b], где a<b. Фигура, ограниченная сверху графиком функции , снизу - осью Ох, сбоку прямыми х=а и х=b называется криволинейной трапецией. Площадь этой криволинейной трапеции найдем, разделив отрезок [a;b] на частичные, как описано выше в 1.1. Составим интегральную сумму для этой функции на данном отрезке:
Каждое
произведение
представляет площадь прямоугольника
со сторонами
,
а сумма площадей прямоугольников
примерно равна площади криволинейной
трапеции. Если n→∞, Sn→
S, где S – площадь криволинейной трапеции:
.
Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
8.3. Формула Ньютона-Лейбница
Теорема. Если функция непрерывна на отрезке [a;b] и F(x) – какая-либо ее первообразная на [a;b], то имеет место формула:
Таким образом, чтобы вычислить определенный интеграл от непрерывной функции на отрезке [a;b], надо найти ее первообразную функцию и взять разность значений первообразной на концах отрезка [a;b].
Примеры:
1)
2)
3)
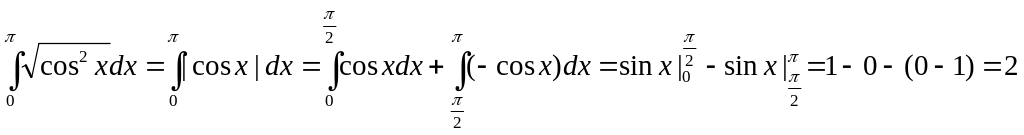
4)
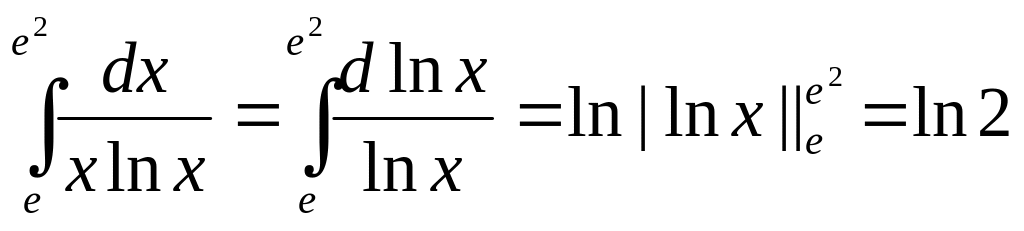
Лекция 9 Свойства определенного интеграла
Пусть задана непрерывная на отрезке [a;b] функция (где a<b). Тогда справедливы следующие теоремы:
1. Постоянный множитель можно выносить за знак интеграла:
,
где с – некоторое число.
2. Определенный интеграл от алгебраической суммы конечного числа непрерывных на отрезке [a;b] функций равен алгебраической сумме определенных интегралов от слагаемых функций:
3. Если в определенном интеграле (где a<b) поменять местами пределы интегрирования, то определенный интеграл меняет знак на противоположный:
4.
Если a<c<b, то
.
Это свойство называется аддитивностью
определенного интеграла.
5. Теорема о среднем. Если функция непрерывна на отрезке [a;b], то внутри отрезка найдется такая точка с, что для нее справедлива следующая формула:
При f(x)≥0 теорема имеет простой геометрический смысл: значение определенного интеграла функции на отрезке [a;b] равно площади прямоугольника с высотой f(c) и основанием (b-a).
6.
Если функция f(x)
сохраняет свой знак на отрезке [a;b], где
a<b, то интеграл
имеет тот же знак, что и функция. Так,
если f(x)≥0
на [a;b], то и
.
7.
Неравенство между непрерывными функциями
на отрезке [a;b] можно интегрировать. Так,
если
,
то
.
Замечание: дифференцировать неравенства нельзя.
8. Оценка интеграла. Если m и М соответственно наименьшее и наибольшее значения функции y=f(x) на отрезке [a;b], то справедливо следующее двойное неравенство:
.
Если f(x)≥0, то геометрический смысл этого свойства заключается в следующем: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых отрезок [a;b], а высоты равны m и М.
9.
Модуль определенного интеграла не
превосходит интеграла от модуля
подынтегральной функции:
.
Так
как
,
то
.
Отсюда и следует указанное неравенство
.
10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом.
Так
как по формуле Ньтона-Лейбница
,
то
.
Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.