Лекция 6 Интегрирование тригонометрических выражений

1. Интегралы вида ; ; ,

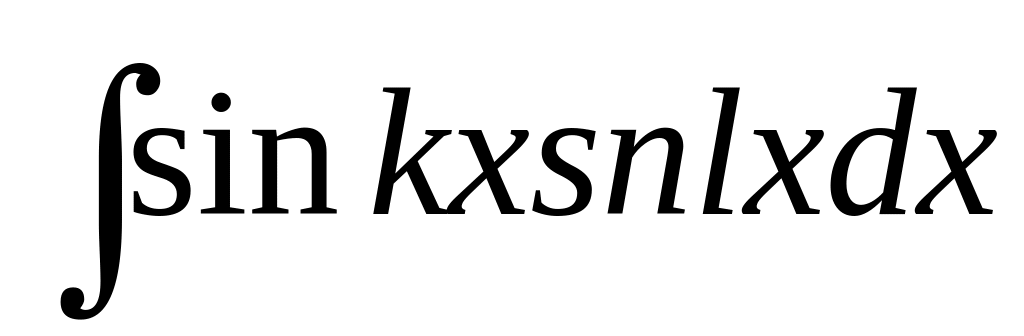где k, l – действительные числа.

Интегралы решаются с помощью применения тригонометрических формул:

Примеры:

1)

2)

3)

2. Интегралы вида

Рассмотрим 4 случая:

1. m – нечетное положительное число, т.е. . Подынтегральное выражение преобразовываем так:

В интеграле переходим к новой переменной интегрирования:

2) показатель степени косинуса n – нечетное положительное число

Тогда:

3) Сумма показателей степеней синуса и косинуса четное отрицательное число .

В этом случае подынтегральная функция может иметь два вида:

- подынтегральная функция дробь, в числителе которой находится степень синуса, а в знаменателе – степень косинуса (или наоборот), причем показатели степени или оба четные или оба нечетные. В этом случае говорят, что они одинаковой четности. Так как - отрицательное число, то отсюда следует, что степень знаменателя больше степени числителя.

- подынтегральная функция дробь, числитель которой постоянная величина, а знаменатель – произведение степеней синуса и косинуса одинаковой четности.

В рассматриваемом случае ( ) любая из подстановок преобразует подынтегральную функцию в многочлен или многочлен, сложенный с целыми отрицательными степенями некоторой независимой переменной t

Если подынтегральная функция имеет первый из разобранных видов, а в числителе находится степень sinx, более удобной из этих подстановок является tgx=t, если же в числителе находится степень cosx, рациональнее применить ctgx=t.

Дроби второго вида с помощью указанных подстановок можно привести к интегрированию степенных функций.

Если применять подстановку tgx=t, надо учесть:

Если применяется подстановка ctgx=t, то

4) Сумма показателей степеней синуса и косинуса равны по абсолютной величине, но противоположны по знаку, а подынтегральное выражение имеет один из видов . Если m>0, то интеграл приводится к виду , а если n>0 – к интегралу .

В первом интеграле применяют подстановку tgx=t, .

Во втором интеграле применяют подстановку сtgx=t, .

Примеры

1)

2)

3)

4)

5)

Лекция 8 Определенный интеграл

8.1. Определенный интеграл как предел интегральной суммы

Пусть дана функция , определенная на отрезке [a;b], где a<b. Разобъем отрезок [a;b] на частичные отрезки произвольной длины [x₀;x₁], [x₁;x₂],…, [x_n-1;x_n], так что x₀=a, x_n=b (x₀<x₁<…<x_n). На каждом частичном отрезке выбираем произвольную точку и вычислим значения функции в каждой из этих точек . Составим произведения , где - длина частичного отрезка. Составим сумму всех таких произведений:

Эта сумма называется интегральной суммой функции на отрезке [a;b].

Обозначим частичный отрезок наибольшей длины . Будем увеличивать число разбиений отрезка [a;b] на частичные отрезки, т.е. n→∞, не изменяя длину самого отрезка [a;b]. При этом →0. Найдем при этих условиях . Предел частичной суммы, если он существует, не зависит ни от способа разбиения отрезка [a;b] на частичные отрезки, ни от выбора точек на них. Этот предел называется определенным интегралом от функции на отрезке [a;b] и обозначается:

Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования, [a;b] – область интегрирования.

Теорема Коши. Если функция непрерывна на отрезке [a;b], то определенный интеграл существует.

Непрерывность функции является достаточным условием ее интегрируемости. Однако, определенный интеграл может существовать и для некоторых разрывных функций, в частности, для всякой ограниченной на отрезке функции, имеющем на нем конечное число точек разрыва.

Из определения определенного интеграла следуют свойства:

- определенный интеграл не зависит от обозначения переменной интегрирования = = , так как интегральная сумма не зависит от того, какой буквой обозначить ее аргумент;

- определенный интеграл с одинаковыми пределами интегрирования равен нулю , так как длина отрезка равна нулю;

- для любого действительного числа с: , так как при этом .