Метод неопределенных коэффициентов

Суть метода состоит в следующем. Пусть имеется разложение правильной рациональной дроби на сумму простейших рациональных дробей с неопределенными коэффициентами. Приводят к общему знаменателю простейшие дроби и приравнивают многочлен, полученный в числителе многочлену . Из полученного равенства составляют систему линейных уравнений, приравнивая коэффициенты при одинаковых степенях х слева и справа указанного равенства.

Метод частных значений

Задают переменной х несколько частных значений (по числу неопределенных коэффициентов) и получают систему уравнений относительно неопределенных коэффициентов. Особенно выгодно применять этот метод в случае, когда корни знаменателя дроби просты и действительны. Тогда удобно последовательно задавать х значения, равные корням знаменателя.

Общие правила интегрирования рациональных дробей:

1. Если дробь неправильная, то ее надо представить в виде суммы многочлена и правильной дроби.

2. Разложить знаменатель правильной рациональной дроби на множители, представить дробь в виде суммы простейших рациональных дробей.

3. Интегрируют многочлен и полученную сумму простейших дробей.

Примеры.

1)

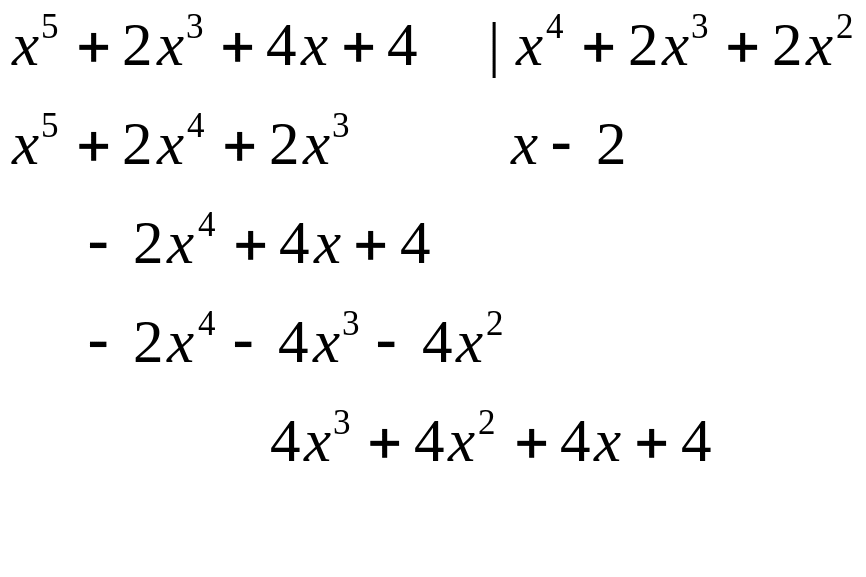
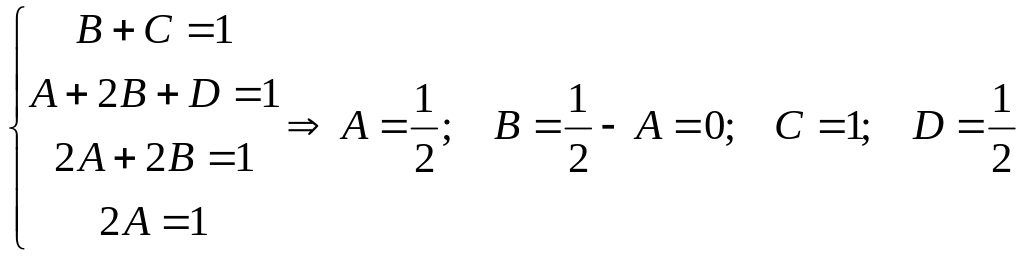
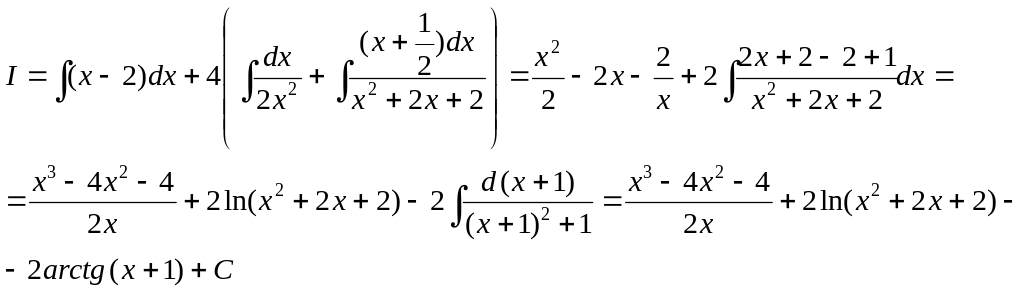
Лекция 5

5 Интегрирование иррациональных выражений

5.1. Интегралы вида

,

где α, β, γ – дробно-рациональные числа.

Интегралы вычисляются постановкой , где n – наименьшее общее кратное знаменателей дробей α, β, γ. С помощью такой подстановки интеграл приводится к интегралу дробно-рациональной функции.

Примеры.

1).

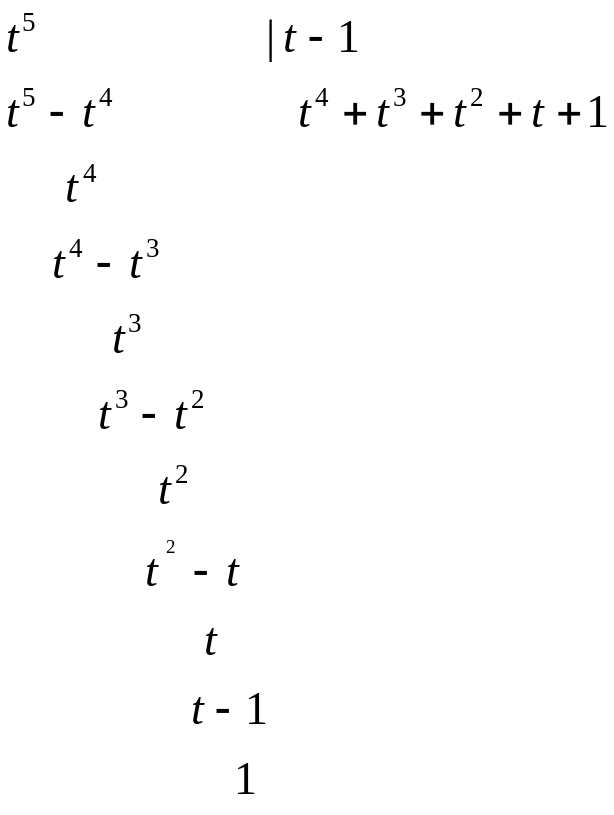
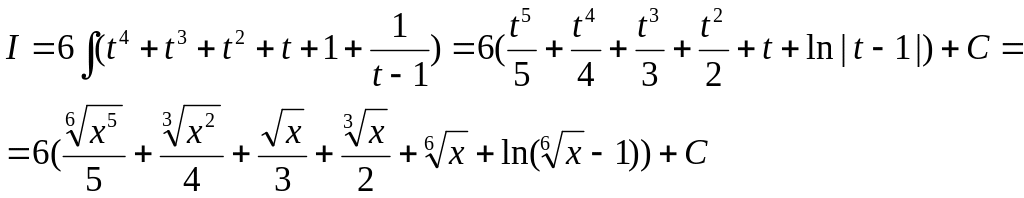
2)

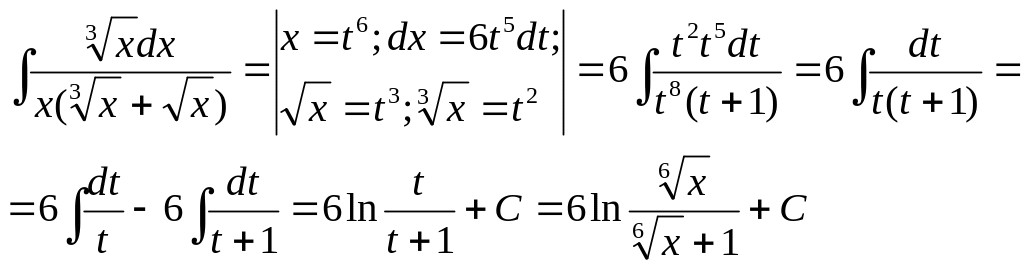
3)

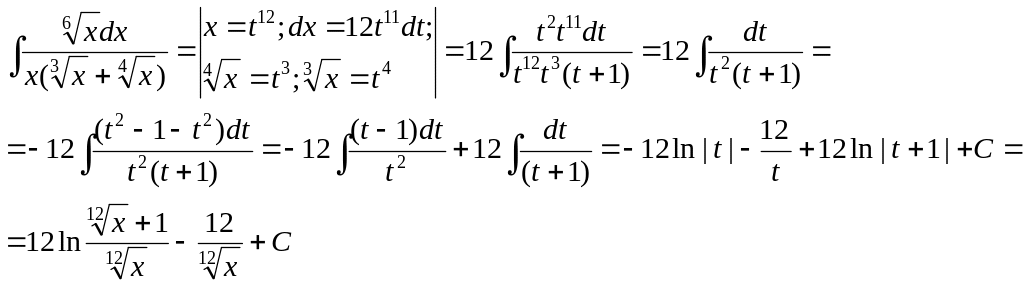
5.2. Интегралы вида

,

где α, β, γ – дробно-рациональные числа.

Интегралы вычисляются постановкой , где n – наименьшее общее кратное знаменателей дробей α, β, γ. С помощью такой подстановки интеграл приводится к интегралу дробно-рациональной функции.

Частным случаем этого интеграла является интеграл с рациональной функций R от линейной функции (ax+b) c различными показателями. Тогда применяется подстановка .

Примеры.

1)

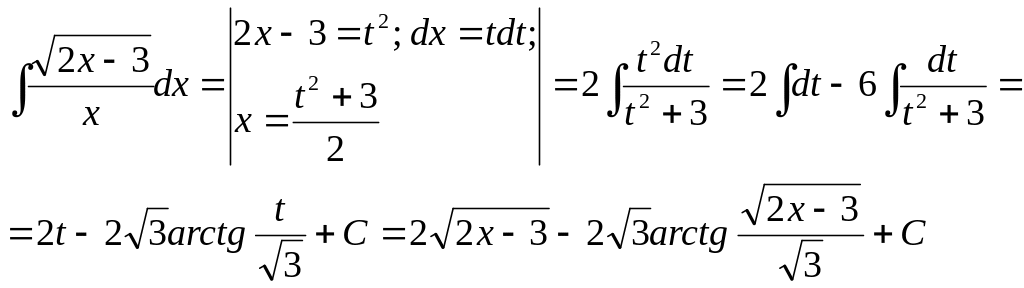
2)

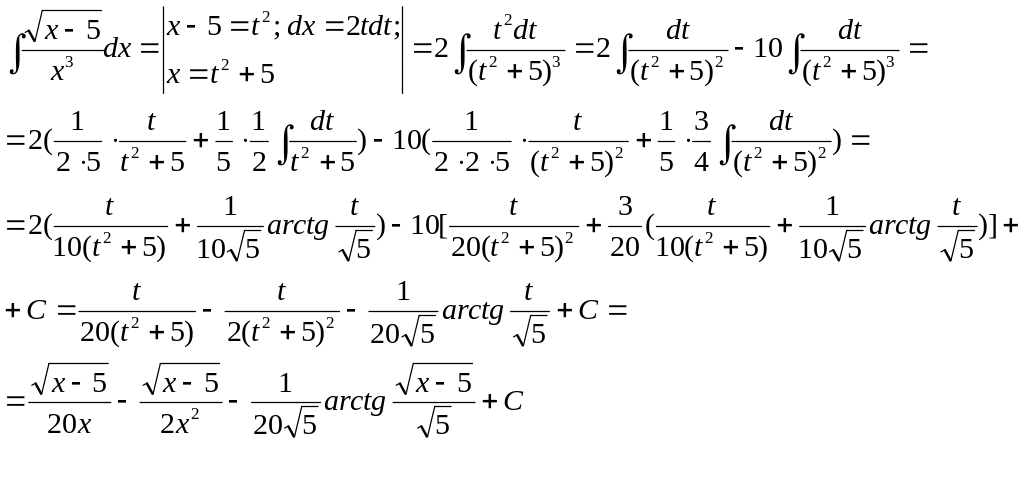
3)

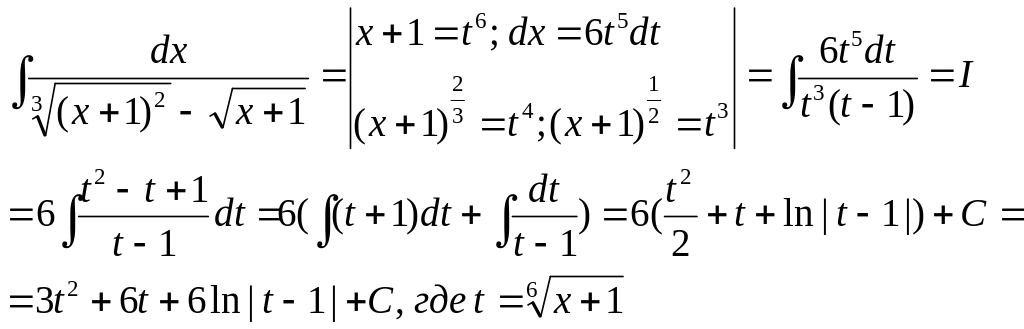
5.3. Применение тригонометрических подстановок для вычисления интегралов вида

Для интегралов, не содержащих других иррациональностей, кроме квадратичного корня из квадратного трехчлена, применяются также тригонометрические подстановки, которые приводят интеграл от рациональной функции синуса и косинуса.

Чтобы применить эти подстановки, следует выполнить ряд преобразований. Из квадратного трехчлена, находящегося под корнем, надо выделить полный квадрат, после чего применить линейную подстановку. Это дает возможность получить под корнем следующие выражения:

1) при a>0 – сумму квадратов вида .или . После того, как под корнем окажется выражение вида (1) для уничтожения иррациональности в подынтегральном выражении следует применить подстановку . Если под корнем окажется выражение вида (2), то для уничтожения иррациональности в подынтегральном выражении надо применить подстановку

2) при a<0 – выражения вида .или . После того, как под корнем окажется выражение вида (3) для уничтожения иррациональности в подынтегральном выражении следует применить подстановку . Если под корнем окажется выражение вида (4), т.е. отрицательное выражение, по подстановки не применяются.

При решении интегралов используются следующие табличные интегралы:

Примеры:

1)

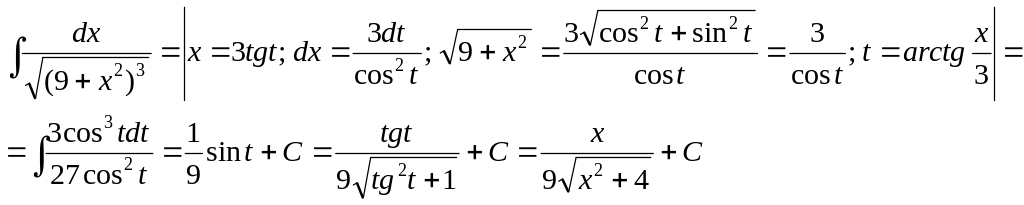
2)

3)