Лекция 3

2. Метод интегрирования по частям

Метод интегрирования по частям следует из формулы дифференциала произведения двух функций. Пусть u(x) и v(x) – две дифференцируемые функции переменной х. Тогда:

. Проинтегрируем это выражение: . Но так как , то:

(3.1)

Формула (3.1) называется формулой интегрирования по частям. Эту формулу применять целесообразно, когда интеграл правой части более простой для вычисления, нежели исходный.

Приведем некоторые часто встречающиеся типы интегралов, вычисляемых этим методом.

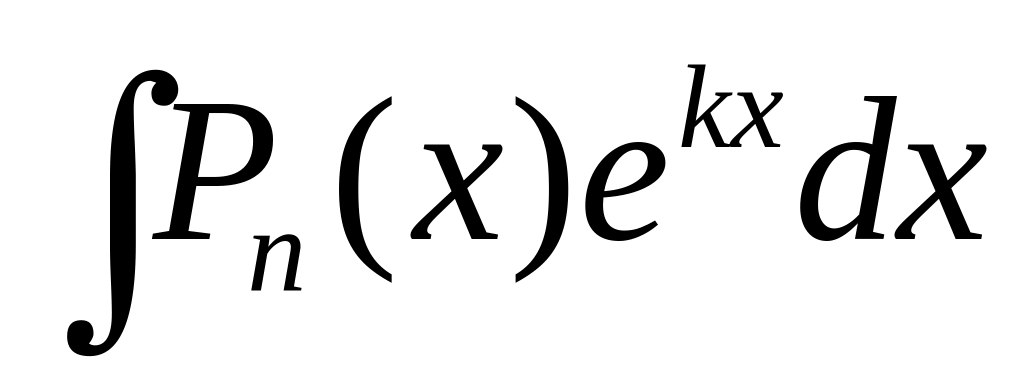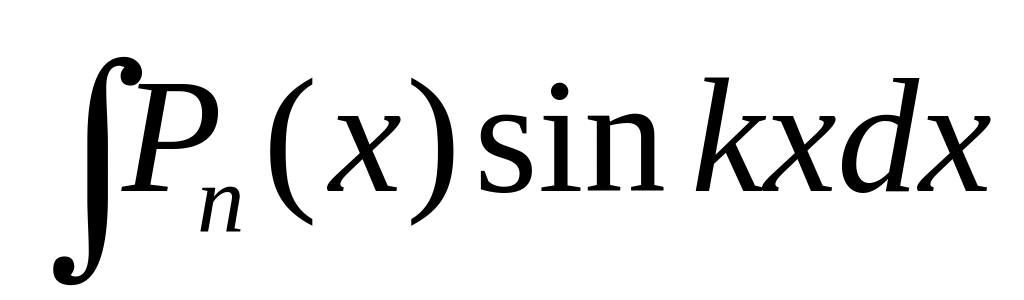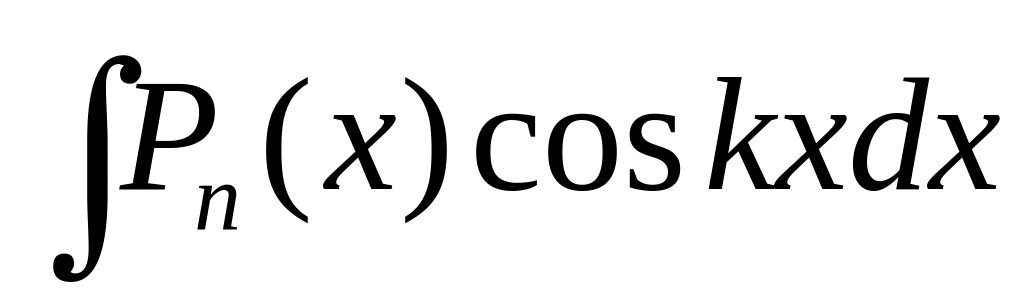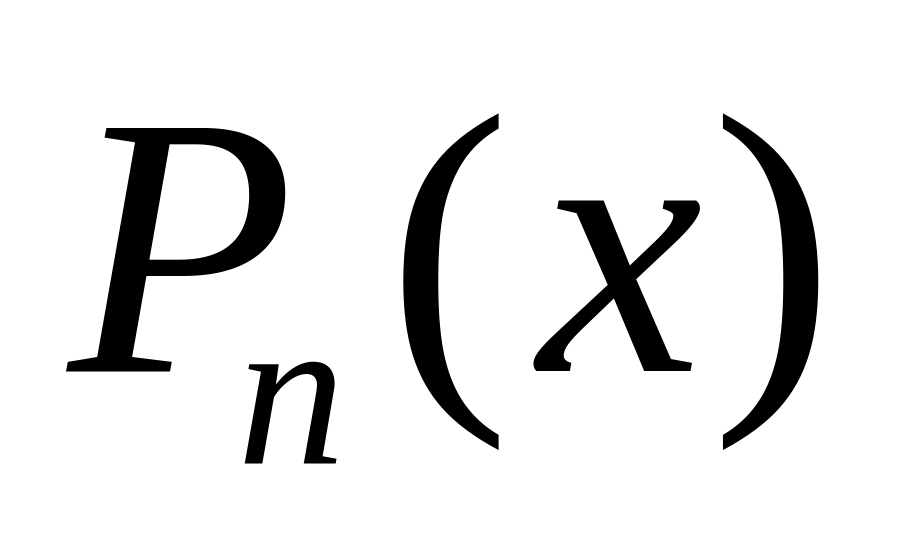1. Интегралы вида ; ; , где - многочлен степени n, k – некоторое число. Чтобы найти эти интегралы, полагают 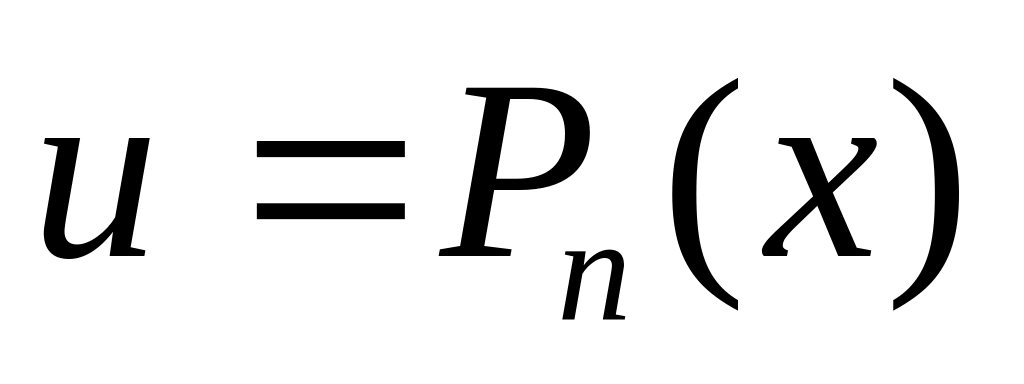, остальное принимают за dv, находят du и функцию v, интегрируя dv, и применяют формулу (3.1) n раз.

2. Интегралы вида 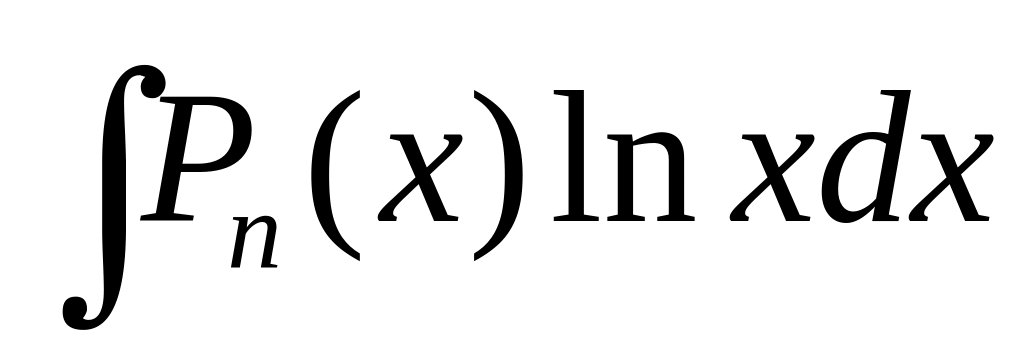; ; ; ; 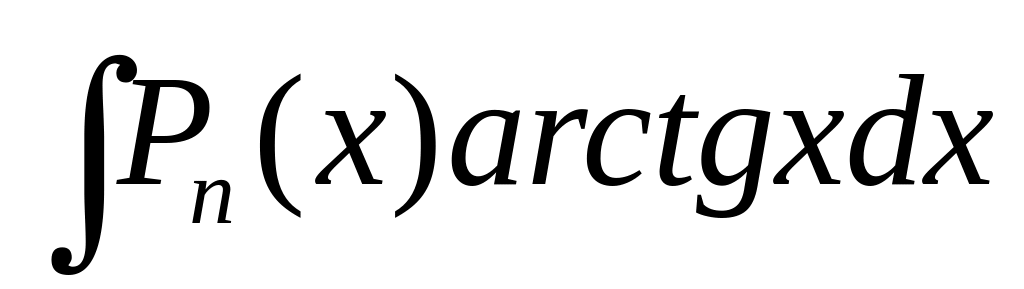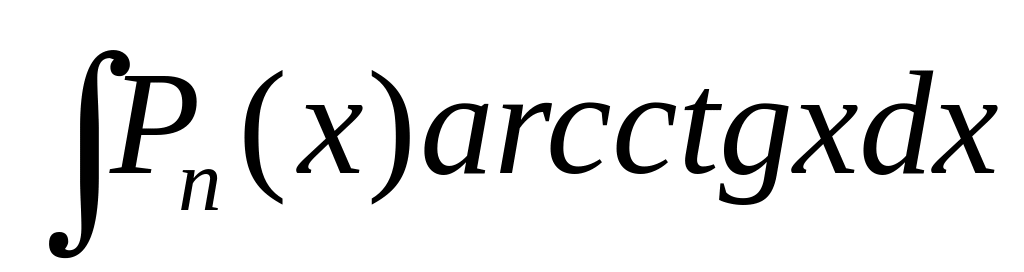. Эти интегралы находят, полагая 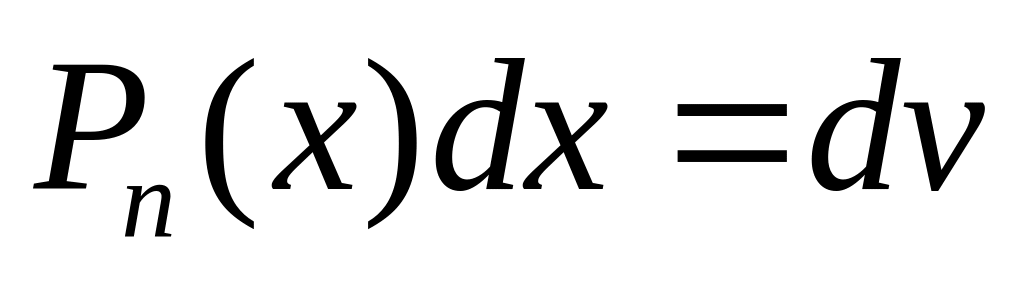, а оставшуюся функцию принимают за u.

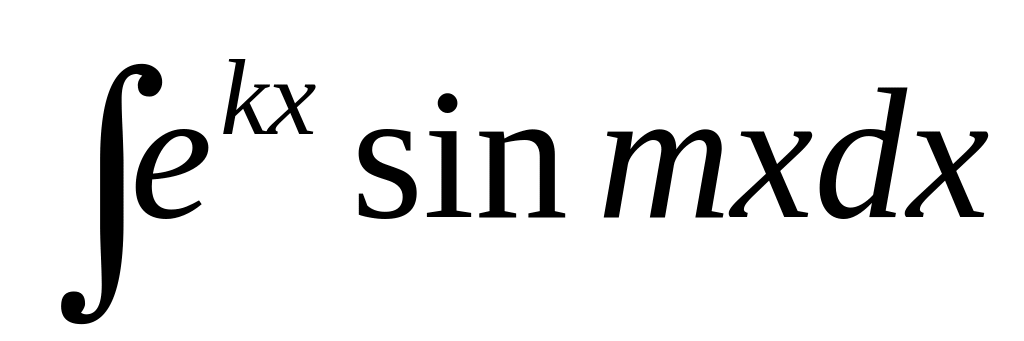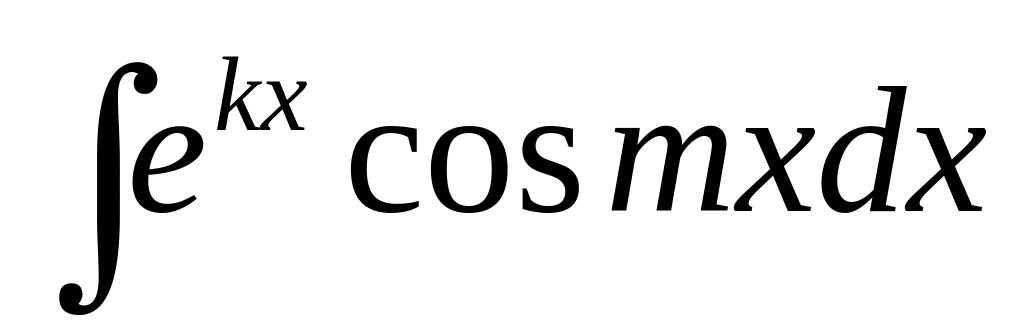3. Интегралы вида ; , где m – некоторое число. За функцию u принимают 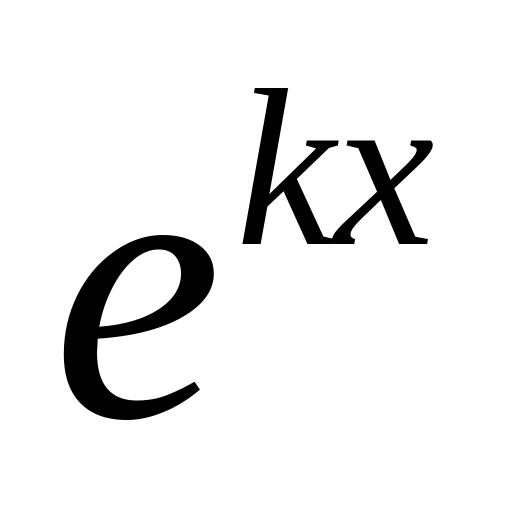, двукратно интегрируют по частям.

Примеры.

1)

2)

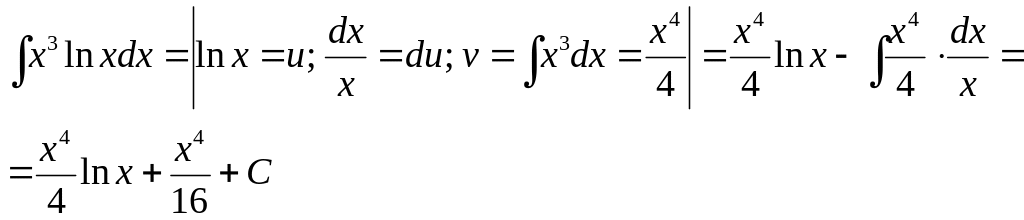
3)

,

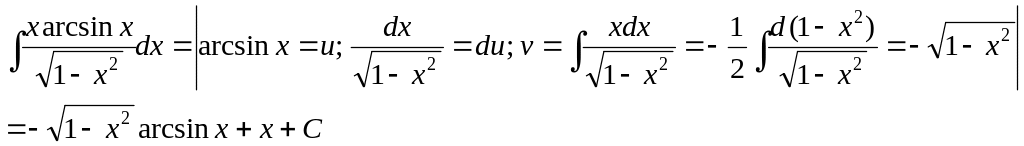
3. Интегрирование простейших рациональных дробей

Существуют 4 типа простейших рациональных дробей:

1. ; 2. ; 3. ; 4. ,

где A, B, k, a, p, q – действительные числа; n=2, 3, 4… ; квадратные трехчлены не имеют действительных корней.

Рассмотрим интегрирование первых трех типов простейших дробей. Интегралы простейших дробей 1 и 2 типа являются почти табличными:

1)

2)

При интегрировании простейших дробей 3 типа сначала выделяют в числителе дроби производную знаменателя, затем разбивают интеграл на два. Первый интеграл – табличный и он равен логарифму знаменателя. Во втором интеграле в знаменателе выделяют полный квадрат, переходят к новой переменной и относительно нее получают табличный интеграл, равный арктангенсу:

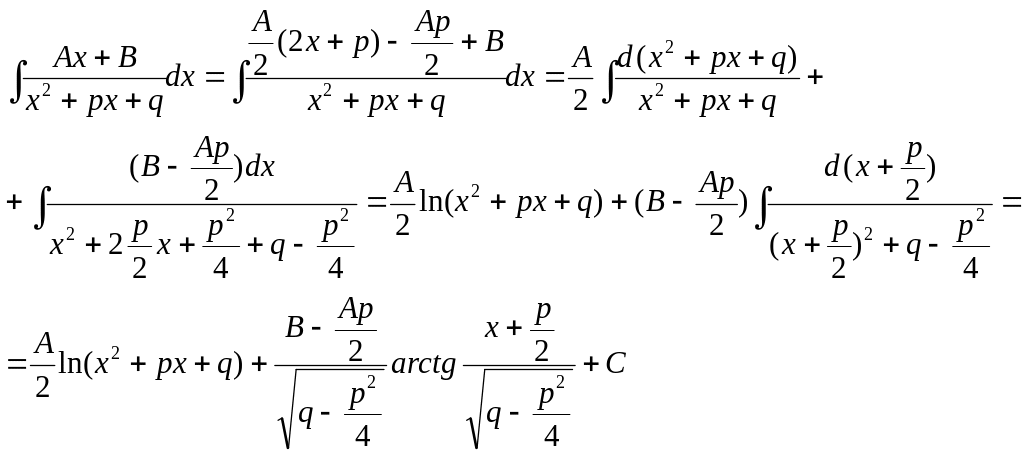
Примеры.

1)

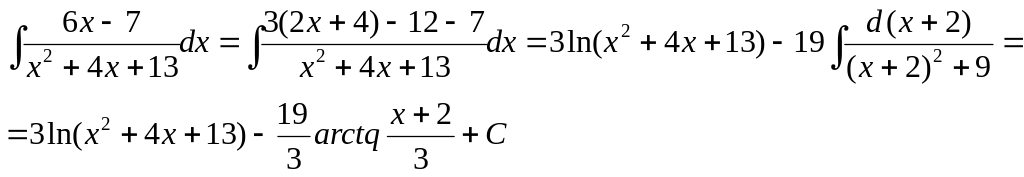
2)

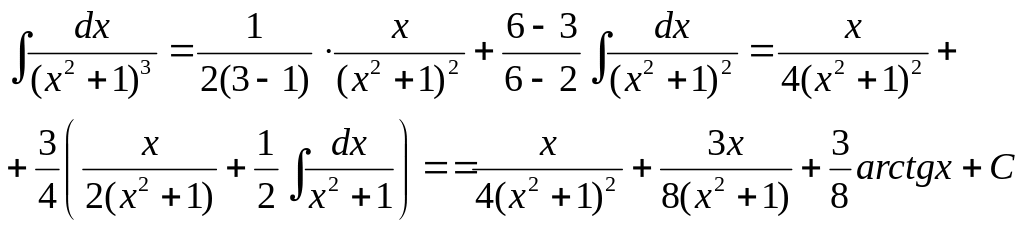
3)

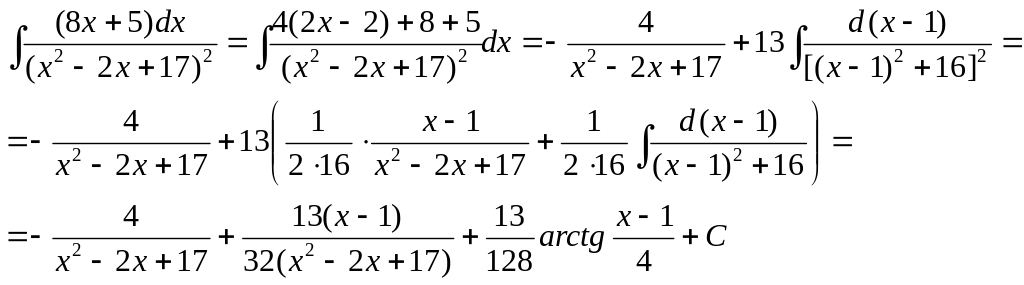
Лекция 4

4. Интегрирование рациональных дробей

Рациональной дробью называется выражение , где и - многочлены n-ой и m-ой степеней соответственно.

Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя: n<m.

Рациональная дробь называется неправильной, если степень многочлена числителя больше или равна степени многочлена знаменателя: .

Теорема. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби путем деления числителя на знаменатель по правилу деления многочленов:

, где - многочлен- частное, - остаток (многочлен степени k<m).

Интегрирование рациональных дробей сводится к интегрированию многочлена R(x) и правильной дроби :

Теорема. Всякую правильную рациональную дробь можно представить в виде суммы конечного числа простейших рациональных дробей четырех типов. Для этого необходимо многочлен знаменателя разложить на линейные и квадратные множители, найдя его корни, т.е.

, где - корни многочлена, , квадратные многочлены вида не имеют действительных корней.

Тогда правильную рациональную дробь можно единственным образом разложить на сумму простейших дробей:

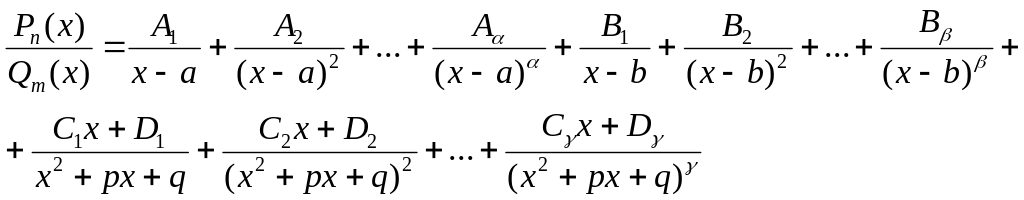, где

- некоторые действительные числа, которые находятся методом неопределенных коэффициентов или методом частных значений. Отметим, что общее число этих коэффициентов равно степени многочлена .