3. Радикальный признак Коши

Теорема. Пусть дан ряд (1) с положительными членами и существует конечный или бесконечный предел . Тогда ряд сходится при l<1 и расходится при l>1.

Пример 6. Исследовать сходимость ряда:

Решение:

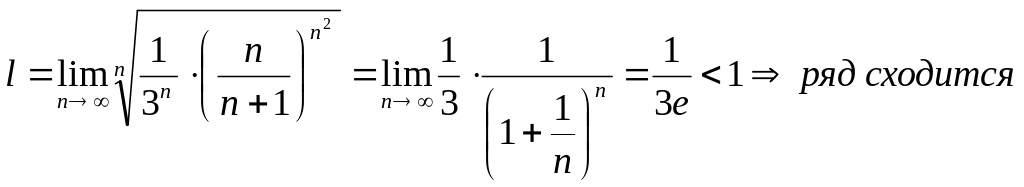
3. Интегральный признак Коши

Теорема. Если члены знакоположительного ряда (1) могут быть представлены как числовые значения некоторой монотонно убывающей на [1;+∞) функции f(х) так, что , то:

1. если 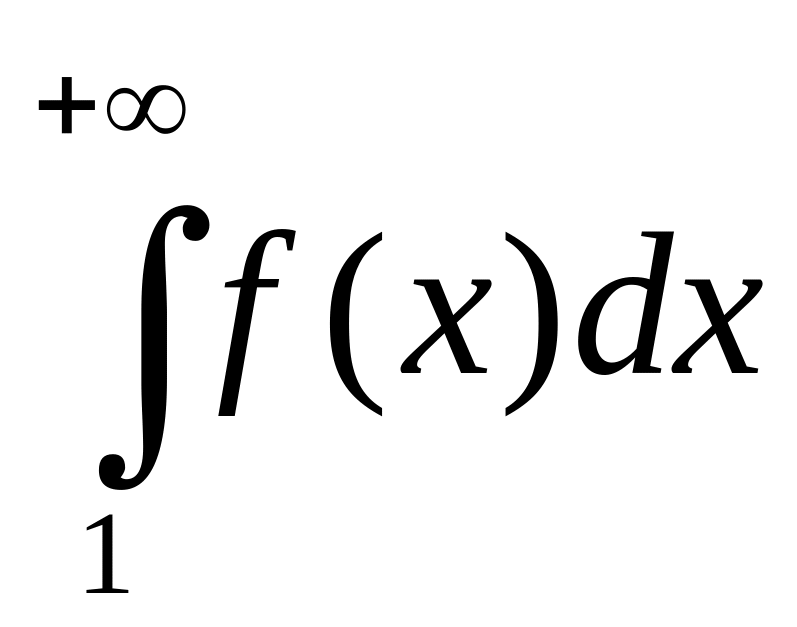сходится, то сходится и ряд (1);

2. если расходится, то расходится и ряд (1)

Замечание: Вместо можно брать . Отбрасывание k первых членов ряда в ряде (1) не влияет на сходимость или расходимость ряда.

Пример 7. Исследовать сходимость ряда:

Решение: Функция удовлетворяет условиям теоремы.

.

Лекция 14 Знакочередующиеся и знакопеременные ряды

Знакочередующимся рядом называется ряд вида:

(14.1).

.

Теорема. Достаточный признак сходимости знакочередующегося ряда. Признак Лейбница.

Знакочередующийся ряд (14.1) сходится, если:

1. Последовательность абсолютных величин членов ряда монотонно убывает, т.е. ;

2. Общий член ряда стремится к нулю: .

При этом сумма S ряда (14.1) удовлетворяет неравенствам:

. (14.2)

Замечания:

1. Исследование знакочередующегося ряда вида 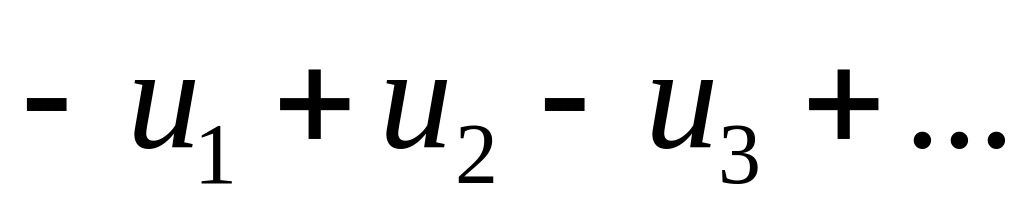(с отрицательным первым членом) сводится к исследованию ряда (14.1) путем умножения всех его членов на «-1»;

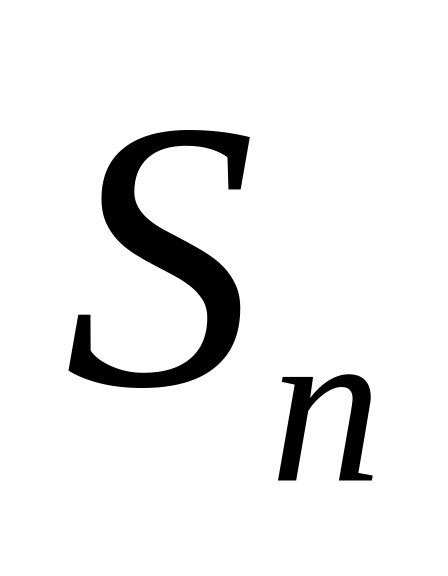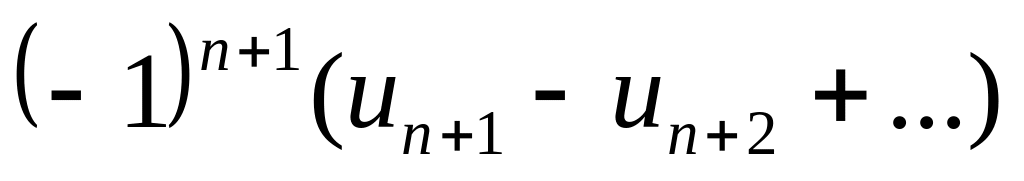2. Соотношение (14.2) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой . Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд , сумма которого по модулю меньше первого члена этого ряда, поэтому ошибка меньше чем модуль первого из отброшенных членов.

Теорема. Общий достаточный признак сходимости знакопеременных рядов.

Пусть дан знакопеременный ряд (2.3). Если сходится ряд, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (2.3).

Замечание: обратное утверждение несправедливо. Если сходится ряд (2.3), то это не означает, что будет сходиться ряд его модулей. Например, знакочередующийся ряд сходится по признаку Лейбница, а ряд, составленный из модулей членов этого ряда. Расходится, так как он является гармоническим рядом.

2.2. Абсолютная и условная сходимости числовых рядов

Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.

Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

В приведенном примере ряд является условно сходящимся, а ряд абсолютно сходится.

Свойства абсолютно сходящихся рядов

1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (Теорема Дирихле. Переместительное свойство).

2. Абсолютно сходящиеся ряды с суммами 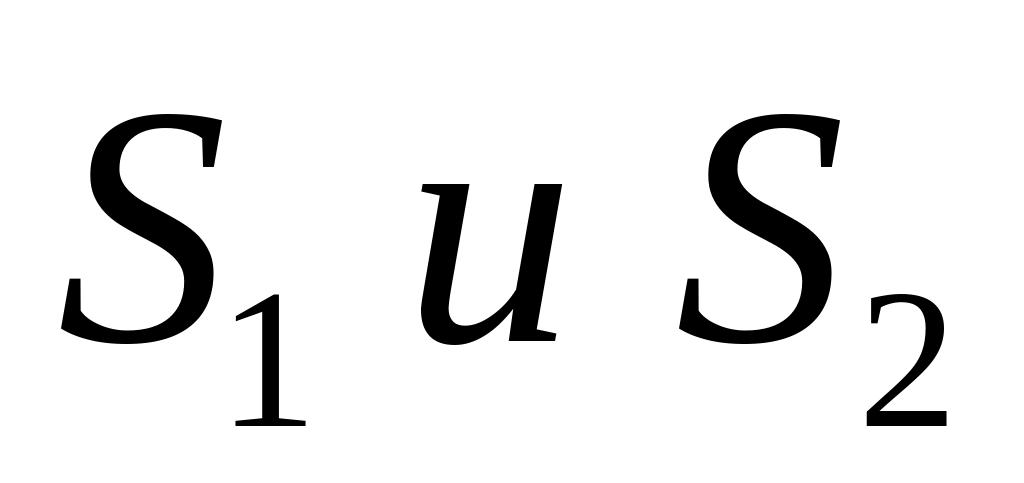можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна 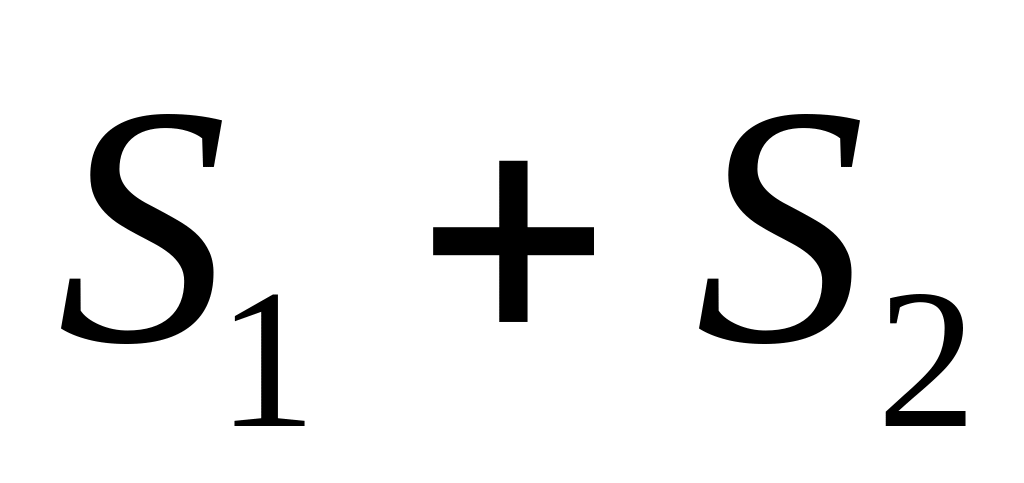(или соответственно ).

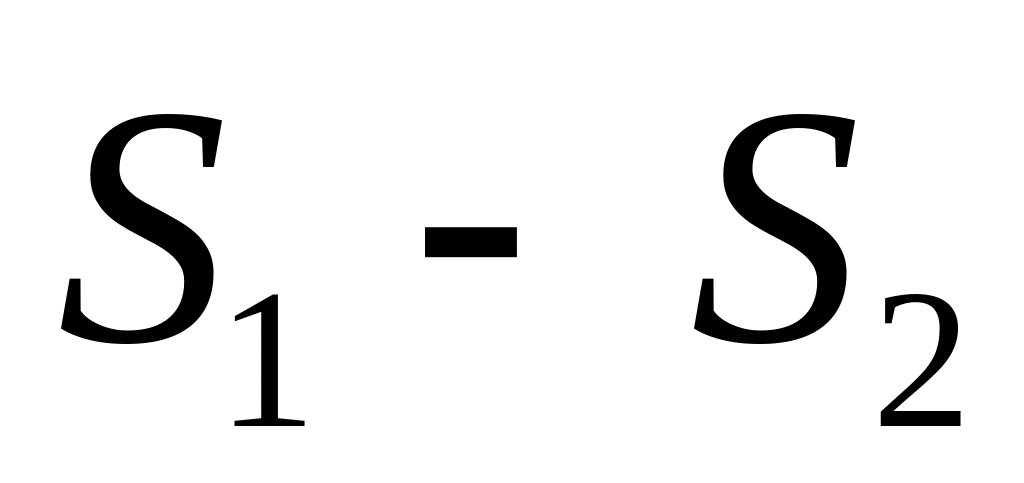3. Произведение двух абсолютно сходящихся рядов с суммами есть абсолютно сходящийся ряд с суммой 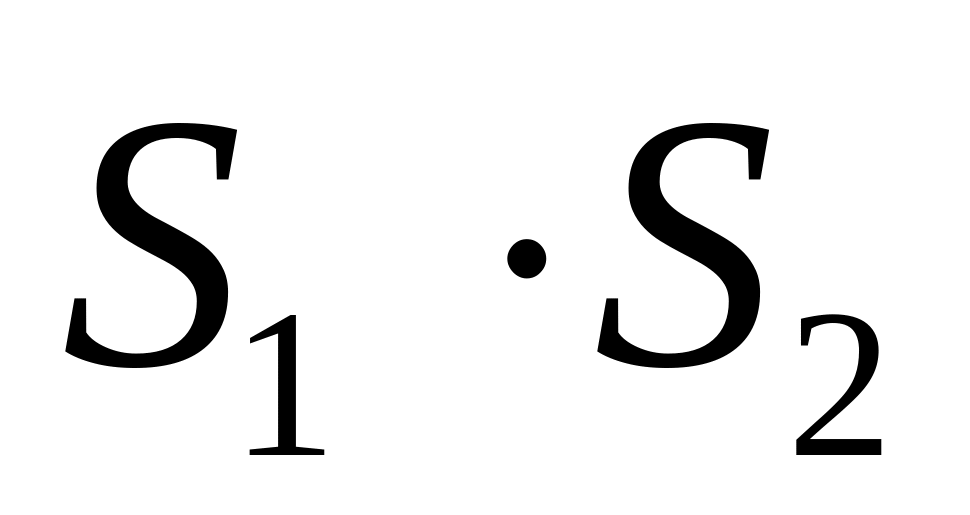. Под произведением двух рядов понимают ряд вида:

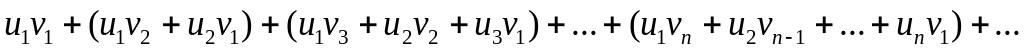
Таким образом, абсолютно сходящиеся ряды суммируют, вычитают, перемножают как обычные ряды. Суммы таких рядов не зависят от порядка записи их членов.

В случае условно сходящихся рядов перечисленные свойства не имеют места. Поэтому действия над рядами нельзя производить. Не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.