2.5 Лабораторная работа № 4 Оптимальный план затрат на рекламу

Цель работы: научиться планировать оптимальные объемы затрат на рекламу для увеличения объема продаж и получения наибольшей прибыли. Освоить методику и технологию оптимизации планов в табличном процессоре Excel с помощью программы Поиск решения (Solver).

Постановка задачи: при разработке годового финансового плана деятельности фирмы для получения наибольшей прибыли необходимо определить расходы на рекламу в 1-м квартале, за год. Определить зависимость продаж от затрат на рекламу, зависимость прибыли от от затрат на рекламу.

Табличная модель

В проблемную систему включаем следующие объекты и показатели:

• планируемые показатели сокращенного баланса расходов, доходов и прибыли фирмы;

• модели (формулы) причинно- следственных связей объемов продаж, доходов и прибыли в зависимости от затрат на рекламу.

Упростим задачу годового планирования и будем определять расходы на рекламу для получения наибольшей прибыли в одном 1-м квартале года (таблица 1). Предполагается, что увеличение рекламы вызывает увеличение продаж без временного лага (запаздывания, последствий, отклоняющего аргумента), т.е. в этом же квартале.

Таблица 1

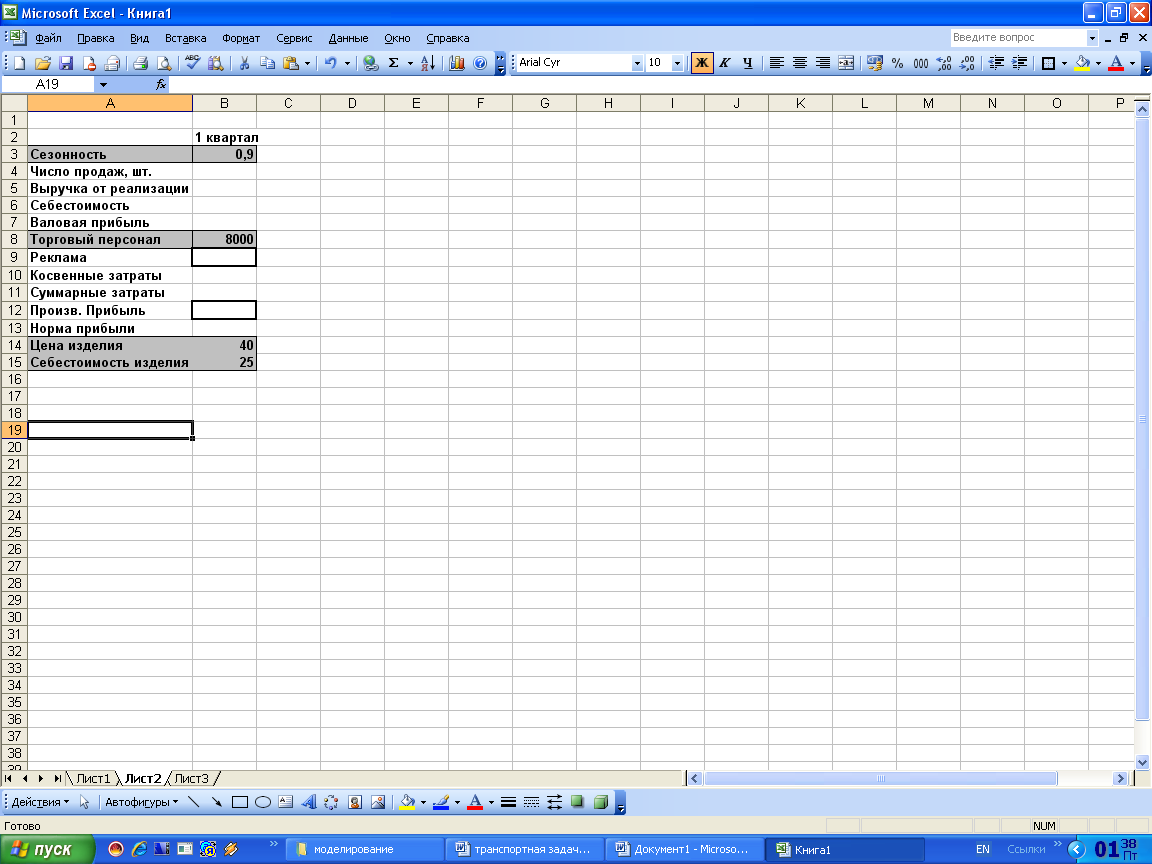
Исходными данными являются коэффициент сезонного изменения объемов продаж, затраты на торговый персонал, цена и себестоимость изделия. Искомыми показателями являются затраты на рекламу и производственная прибыль.

Формулы табличной модели

После составления плановой таблицы необходимо связать показатели формулами для вычислений, как показано в таблице 2

Таблица 2

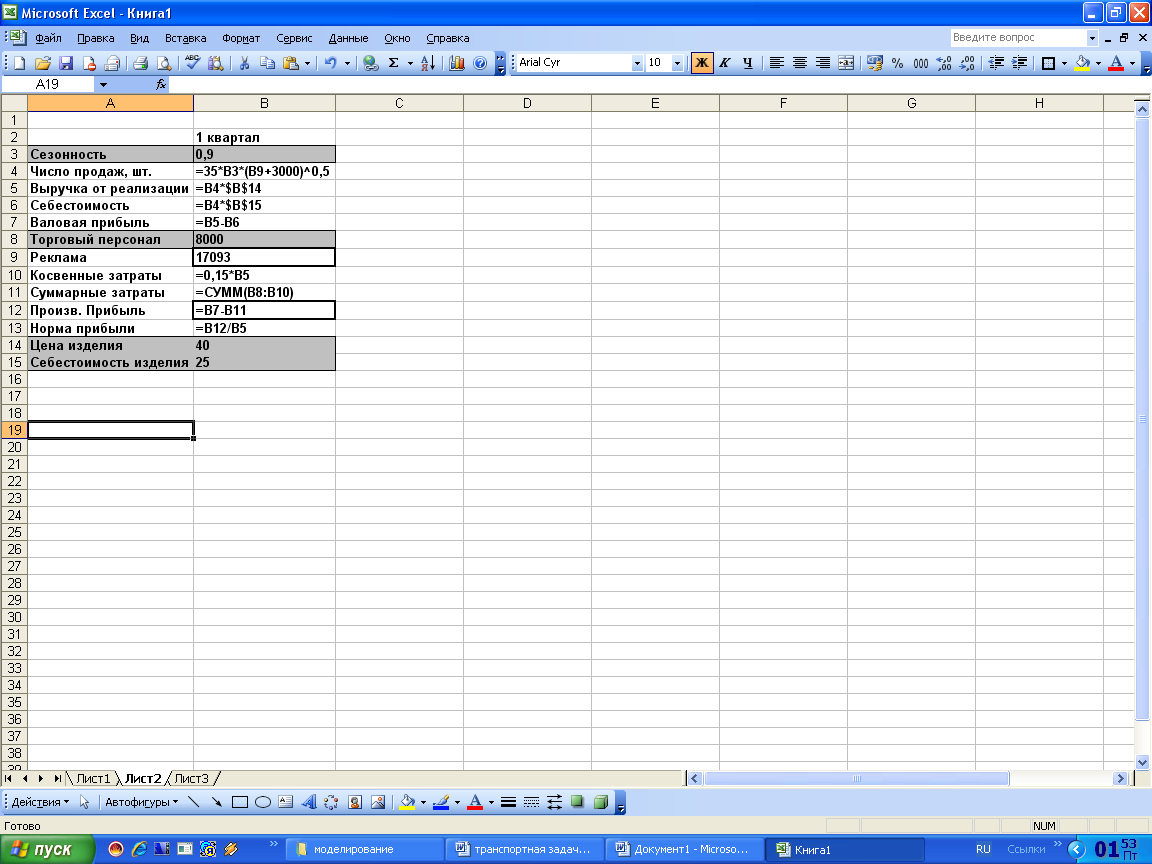
Зависимость продаж от затрат на рекламу

В нашем примере задана формула зависимости объема продаж от затрат на рекламу в ячейке В4:

=35 * В3 * (В9 + 3000) ^ 0,5

Чтобы понять силу влияния факторов, используем график. Для этого составим таблицу влияния фактора с помощью таблицы подстановки для одной функции с одним аргументом (таблица 3).

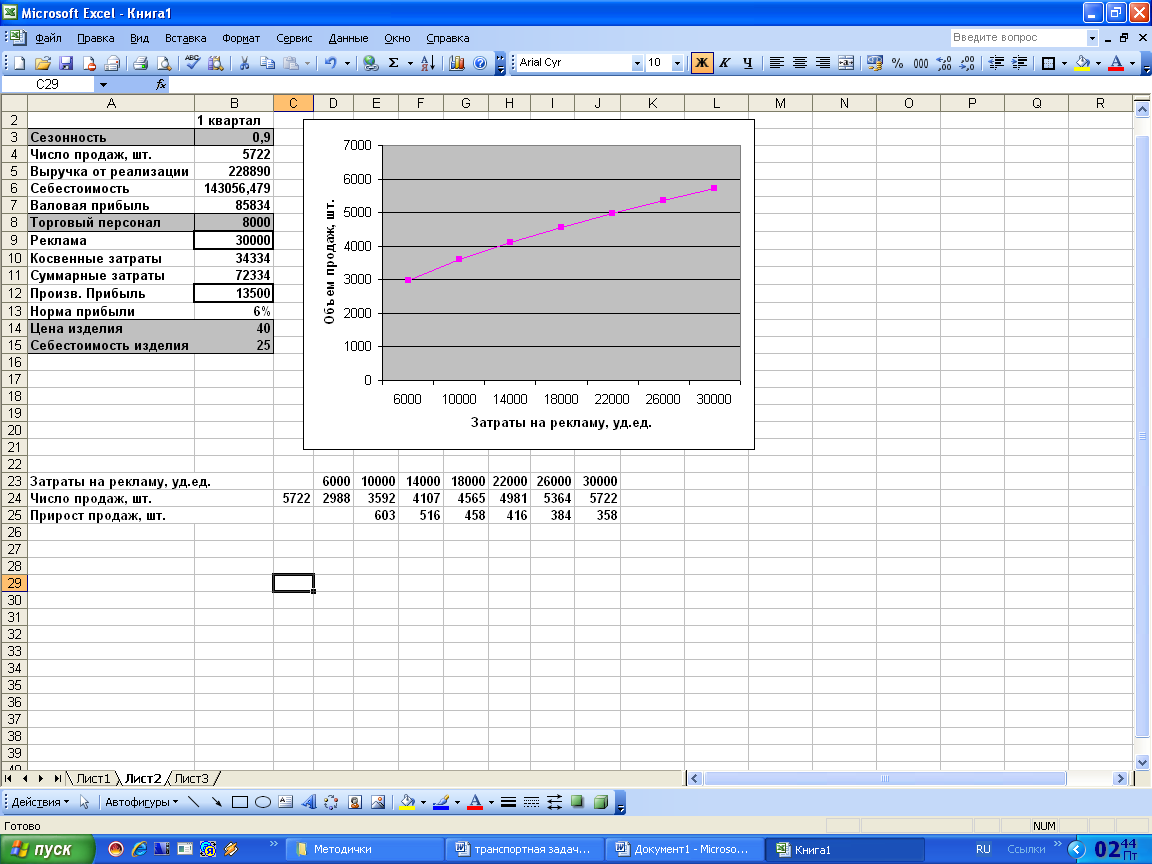
Установим начальное значение затрат на рекламу 6000 в ячейку D23 и будем задавать следующие числа арифметической прогрессии с шагом 4000 (диапазон E23:J23). Получили план однофакторного имитационного эксперимента.

В ячейку С24 введем формулу: =35*В3*(В9+3000)^0,5. Выделим диапазон C23:J24, выполним команду Данные/Таблица подстановки. В окне Таблица подстановки в поле Подставлять значения по столбцам введем адрес ячейки В9, ОК. Строка Число продаж заполнится числами. Заполнить строку Прирост продаж (E24-D24).

Построить график: выполнить команду Вставка/Диаграмма, указать тип диаграммы- График., Далее. Перейти во вкладку Ряд, щелкнуть кнопку Добавить, в поле Значения ввести диапазон $D$24:$J$24. В поле Подписи по оси Х ввести диапазон $D$23:$J$23, Далее.

В поле Ось Х ввести текст «Затраты на рекламу, уд.ед.». В поле Ось Y ввести текст «Объем продаж, шт.», Далее, Готово (таблица 3).

Анализируя зависимость продаж от затрат на рекламу определяем, что с ростом затрат растут продажи, экстремума нет. Значит, оптимального решения в этой системе невозможно. Крутизна зависимости с ростом затрат убывает, т.е. наблюдается убывающая эффективность фактора. Для количественной оценки убывающей эффективности фактора используем строку Прирост продаж. На интервале исследования прирост продаж убывает от 600 до 300.

Таблица 3