Теория вероятности и математическая статистика.

Часть I. Случайные события.

Основные понятия:

Случайные события - это события, которые либо происходят, либо нет.

Теория вероятности изучает закономерности случайных явлений, появляющихся при многократном повторении события в условиях случайного эксперимента (совокупности условий, при которых что-то происходит или не происходит).

Элементы комбинаторики.

Комбинаторика – наука о методах подсчёта различных комбинаций.

1. Правило умножения – если объект А можно выбрать m способами, объект B – n способами, то число пар объектов А и В равно m*n.

2. Размещение (из n элементов по m) –это упорядоченный набор m элементов взятых из n элементов. Важен порядок и состав:

   1. Частным случаем является перестановка – упорядоченный набор из всех элементов.

3. Сочетание(из n по m элементам) – это неупорядоченный набор из m элементов, взятых по n элементам. Число всех сочетаний вычисляется по:

Случайным называют событие, которое может произойти или не произойтив результате некоторого опыта.

Совокупность всех условий, при которых возможна реализация случайного события, носит название случайного эксперимента. Примеры:

• Бросание монеты

• Бросание кубика

• Вытаскивание шарика их урны

• Вытаскивание карты из колоды

Элементарные события.

Некоторые из случайных событий можно разложить на более простые.

Пример:

При бросании кубика выпало чётное число очков – составное событие.

Т.е. события, которые нельзя разделить на более простые события называются элементарными событиями или элементарными исходами случайного эксперимента.

Совокупность всех элементарных исходов эксперимента носит название «Пространство всех элементарных исходов случайного эксперимента».

Т.е. элементарные исходы, при которых реализуется событие А, называется элементарными исходами, благоприятствующими наступлению события А или просто благоприятными исходами.

Классификация случайных событий.

Достоверное события – это событие, которое обязательно произойдёт в данном случайном эксперименте.

Невозможное событие – событие, которое никогда не произойдёт в данном случайном эксперименте.

Событие удобно изображать в виде множества из плоскости.

События А и В называются несовместными, если они не могут произойти одновременно в одном и том же случайном эксперименте.

Действия над событиями.

Объединением двух событий А и В называется новое событие, которое заключается в наступлении хотя бы одного их них : А+В

Пересечением двух событий А и В называется новое событие, состоящие в одновременном наступлении этих двух событий.

Разностью называется новое событие, состоящее в том, что А произойдёт, а В –нет.

А называется противоположным В, если оно считается наступившим только тогда, когда В не наступает.

Вероятность случайного события.

Вероятность – численная мера возможности реализации случайного события.

Учитываем, что:

• Вероятность достоверного события = 1; p(Ω)=1

• Вероятность невозможного события = 0; p( 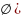=0

• Все прочие значения вероятности лежат между этими крайностями: 0≤p(A)≤1

Существует два подхода к определению вероятности:

• Классический

• Статистический

Классическая схема:

Данная схема обладает следующими свойствами:

1. Пространство элементарных событий (исходов) конечно;

2. Все исходы равнозначны.

Определение:

Вероятность. события А называется отношение числа исходов, благоприятствующих событию А, к общему числу равнозначных исходов:

P(A= ), где n – общее число сходов, а m - число благоприятных исходов.

Статистический подход:

Данный подход обладает следующими свойствами:

1. Используется при возможном многократном эксперименте при неизменных условиях;

2. Можно принять, что вероятность события А равна

Геометрическая схема.

Геометрическая вероятность позволяет рассматривать случайные события с бесконечным числом исходов. Геометрической вероятностью события называется отношение меры области благоприятствующей появлению события, к мере своей области:

p(A)=