Лабораторная работа № 3

Определение коэффициента диффузии водяных паров в воздухе.

Цель работы: определить коэффициент диффузии паров воды в воздухе по испарению капли.

Теоретический материал: явления переноса, кинематические характеристики молекулярного движения, длина свободного пробега, экспериментальное определение поперечного сечения столкновений, диффузия, теплопроводность, вязкость идеального газа.

Основное уравнение явлений переноса.

Равновесное состояние газа в молекулярно-кинетической теории рассматривается как состояние полной хаотичности движения молекул, распределение которых по скоростям подчиняется закону Максвелла. Любое нарушение равновесия всегда связано с нарушением хаотичности движения и максвелловского распределения по скоростям. Основной особенностью неравновесных состояний является стремление газа самопроизвольно переходить к равновесному состоянию. Это обусловлено хаотическим тепловым движением молекул и непрерывными их столкновениями, которые приводят к постоянному перемешиванию молекул, изменению их скоростей и энергий.

Переход газа в равновесное состояние всегда связан с направленным переносом массы, импульса и энергии. Поэтому соответствующие процессы объединены под общим названием явлений переноса.

Каждое явление переноса бывает обусловлено неодинаковостью значений некоторой физической величины (концентрации, температуры) в разных точках пространства. Если в различных частях объёма газа, его плотность неодинакова, то с течением времени происходит выравнивание плотностей. Это явление называют диффузией. В этом случае переносимой физической величиной является масса. Из области газа с большей плотностью молекулы диффундируют в область с меньшей плотностью.

Если в разных частях объема различна температура, то происходит постепенное её выравнивание за счет переноса молекулами энергии. Соответствующее явление называется теплопроводностью.

Наконец, при ламинарном течении газа между отдельными его слоями в результате теплового хаотического движения молекул происходит перенос молекулами своего импульса. В результате, между слоями газа возникает внутреннее трение. Поскольку механизм перечисленных процессов одинаков, то и уравнение, описывающее эти процессы, будет общим.

Выведем общее уравнение переноса, не конкретизируя, какую именно величину переносят молекулы. Обозначим эту величину через φ, то есть φ – это может быть и масса, и импульс, и энергия молекулы. В случае равновесного состояния φ постоянна по объему газа. При наличии неоднородностей в газе, например, по концентрации или температуре, возникает градиент величины φ и имеет место поток этой величины в направлении его уменьшения.

Рис. 1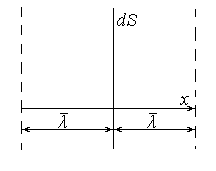

Выделим в газе площадку dS, перпендикулярную оси x, вдоль которой поддерживается, например, постоянная разность концентраций или температуры, или, в общем случае, градиент физической величины φ. Поскольку обмен значениями φ(х) происходит только при взаимодействии молекул, то есть на расстоянии порядка средней длины свободного пробега λ, то и значение φ(х) можно считать неизменным лишь на расстоянии λ слева и справа от площадки dS. Поскольку λ – величина достаточно малая, то φ(х) можно разложить в ряд по степеням этой величины и, ограничившись членом первой степени малости, записать:

В предположении, что тепловые скорости молекул не зависят от направления и их средние значения равны , можно записать, что поток молекул в направлении оси х равен , где n₀ – равновесная концентрация молекул.

Следовательно поток физической величины φ через площадку dS в направлении отрицательных значений х равен:

а в направлении положительных значений

Полный поток в положительном направлении оси х в любой точке будет равен:

(1)

Это уравнение является основным уравнением процессов переноса.

Если в некотором объеме газа имеется неоднородность плотности, то возникает диффузия. Переносимой физической величиной в этом случае является масса молекулы m. С учетом из уравнения (1), получаем уравнение стационарной диффузии или закон Фика:

(2)

Величину называют коэффициентом диффузии.

При фиксированной температуре , a , следовательно, Если постоянно давление, то , a . Значит . Соотношение , которое удобно записать в виде DP=Const, соблюдается в достаточно широком интервале давлений для не очень плотных газов с точностью до нескольких десятков процентов. В зависимости от температуры D растет несколько быстрее, чем Т^3/2.

Значения коэффициентов диффузии газов необходимо знать для расчета различных диффузионных процессов в физико-химической гидродинамике. Например, для расчета процессов горения жидких и твердых топлив, процессов смешения газов и т.п.

Расчет испарения капли в неподвижной среде. Изучение кинетики испарения капель различных жидкостей позволяет экспериментально определить коэффициенты диффузии паров.

Пусть сферическая капля воды с начальным радиусом R₀ находится в воздухе с относительной влажностью f при температуре Т. Скорость испарения капли определяется скоростью диффузии пара из приповерхностного слоя и количества тепла, поступающего к капле извне благодаря теплопроводности и расходуемого на ее исчерпание. Будем считать процесс испарения квазистационарным. На поверхности капли ее пар является насыщенным, температура капли постоянна. Тогда масса dm пара, диффундирующего через произвольную сферическую поверхность радиуса r, концентрическую с поверхностью капли, равна:

(3)

где ρ – плотность пара.

Так как процесс квазистационарный, то эта величина не будет зависеть от r . Это приводит к уравнению

, где

После интегрирования получим , где - плотность пара на бесконечном удалении от капли.

Величину А можно найти, приняв во внимание, что на поверхности капли пар насыщенный, то есть, что при r=R и, следовательно, ρ=ρ_нас,

А=R(ρ_{нас -} ρ_∞)

Тогда

С другой стороны радиус капли R меняется в процессе ее испарения и поэтому

(ρ_ж – плотность жидкости).

Сопоставляя эти два выражения для dm/dt , получим

Пренебрегая зависимостью ρ_нас от кривизны поверхности капли, то есть для достаточно крупных капель, найдем после интегрирования

или, если известна относительная влажность,

Таким образом, процесс испарение капли описывается линейным законом изменения ее площади поверхности с течением времени. Этот закон впервые установил Срезневский.

Комплекс называется константой скорости испарения.

Задачей теоретического анализа процесса испарения является выявление зависимости К от свойств жидкости, среды и условий испарения. Мы ограничимся экспериментальным определением константы скорости испарения в простейшем случае неподвижной среды для вычисления коэффициента диффузии водяного пара.

Методика проведения эксперимента.

В соответствии с линейным законом испарения капли квадрат ее диаметра

(4)

Таким образом, если экспериментально проследить за изменением диаметра испаряющейся капли во времени и построить график зависимости d²=f(t), то из графика легко получить значение константы скорости испарения по тангенсу угла наклона прямой d²(t) к оси абсцисс. Определив температуру среды и капли и измерив относительную влажность воздуха, можно рассчитать коэффициент диффузии водяного пара в воздухе

(5)

Определим из таблиц давление насыщенных паров при температуре Т, тогда, используя соотношения

выражение (5 ) можно записать в виде

μ - молярная масса воды, R – универсальная газовая постоянная, Т – температура капли.

Экспериментальная установка представляет собой камеру с прозрачными стенками, внутри которой на спае термопары с помощью пипетки подвешивается капля воды. С помощью микроскопа следят за уменьшением диаметра капли в процессе испарения.

Эксперимент выполняется в следующем порядке.

1. По термометру, находящемуся в камере, определяют температуру среды Т_∞

2. Относительную влажность воздуха в камере регистрируют по показаниям гигрометра.

3. С помощью пипетки на спай термопары подвешивают каплю воды.

4. По показаниям термопарного гальванометра определяют разность температур среды и капли (Т_∞ - Т).

5. С помощью микроскопа определяют начальный диаметр капли. Увеличение микроскопа определяют перед началом опыта.

6. Включают секундомер и через равные промежутки времени регистрируют диаметр испаряющейся капли. Данные заносят в таблицу. В опытах необходимо получить не менее 10 значений диаметра d для 5 различных капель.

T	0	t1	t2	t3	t4	t5
D	D0	d1	d2	d3	d4	d5

7. По результатам экспериментов строят зависимости d²=f(t) для каждой капли и определяют константу скорости испарения, используя закон Срезневского (4).

8. Формулы (5) и (6) позволяют рассчитать коэффицинты диффузии паров воды по скоростям испарения каждой капли.

9. По полученным для каждой капли коэффициентам диффузии определяют погрешность серии экспериментов в соответствии с теорией погрешностей.

10. В заключение необходимо рассчитать коэффициент диффузии паров воды по формуле и сравнить с экспериментально найденным.