2. Методика измерений и обработка результатов.
Если наблюдаемый случайный процесс для любых временных выборок характеризуется одной и той же функцией распределений плотности вероятности, то такой процесс называют стационарным прив ероятностном подходе описания процесса. На практике применяют более мягкое определение стационарного процесса. Считают, что если первый и второй статистические моменты случайной величины не низменны во времени, то такой процесс называют стационарным. На рисунке 7 видно, что среднее значение остается постоянным, для разных временных выборок случайной величины.
Рис.7.
Иллюстрация стационарного случайного
процесса.
Среднее значение случайной величины приведенной выборки оказывается постоянной величиной, не меняющейся со временем.
Для регистрации космического излучения в данной работе используется счетчик Гейгера-Мюллера, который состоит из следующих блоков:
Датчика космического излучения
Счетного устройства, работающего в накопительном режиме
Блоков питания
Датчик космического излучения представляет собой стеклянную трубку, покрытую внутри металлическим пластом (катод), и тонкую металлическую нить, размещенную вдоль осы трубки (анод). Трубка заполнена аргоном. Действие счетчика базируется на ударной ионизации атомов аргона. Космическая частичка, пролетая в газе, отрывает электрон от атомов и таким образом создает положительные ионы и свободные электроны. Электрическое поле между катодом и анодом ускоряет электроны до энергий, при которых начинается ударная ионизация. Возникает лавина ионов, и ток резко возрастает. Полученный при этом импульс тока усиливается, а потом регистрируется счетным устройством. Временные промежутки, в которых проводится подсчет импульсов, фиксируется обычным секундомером.
3. Порядок выполнения работы.
1. Включите прибор нажатием кнопки “Сеть” на передней панели и дайте ему прогреться (2-3 минуты).
2. Проверьте надежность работы пересчетного устройства, нажав кнопку “Сброс”, а потом “Проверка “. При этом на вход пересчетной схемы подается сменное напряжение с частотой 50 Гц. Через минуту остановите счет, нажав кнопку “Стоп”. Число импульсов должно быть равным Установочному числу с отклонением не большее 1. Повторите измерения 2-3 раза.
Обычно Установочное число равно 3000
3. Нажмите кнопку “Сброс”, а потом “Пуск” и одновременно включите секундомер. Прибор начнет считать импульсы, которые поступают от счетчика.
4. Через каждые 10 секунд, на протяжении 1 часа 30 минут записывайте показания прибора, не останавливая секундомер и счетное устройство, например: 0, 5, 8, 12, 15, 21, 23, 30 и т.д.
5. Из полученных значений найдите число отсчетов , которые регистрируются счетчиком каждые 10 секунд. Для этого из каждого следующего значения отнимите предшествующее, например, 5-0=5, 8-5=3, 12-8=4,15-12=3 и т.д. Поделив на 10, получим набор интенсивностей космического излучения в лаборатории . Таких измерений должно быть не менее N=400.
6. Используя полученные данные, составьте следующую таблицу:
|
|
|
|
|
|
|
0 1 2 3 4 ... |
0,0 0,1 0,2 0,3 0,4 ... |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь
- число частичек, которые попадают в
счетчик за
;
- число выбросов с данной интенсивностью,
находятся путем выборки ответственного
значения из полного набора
данных;
- число импульсов в единицу времени, то
есть интенсивность излучения;
- плотность достоверности интенсивности;
ширина
интервала (в рассмотренном примере
).
7. Из табличных значений найдите средне
статистические значения интенсивности
,
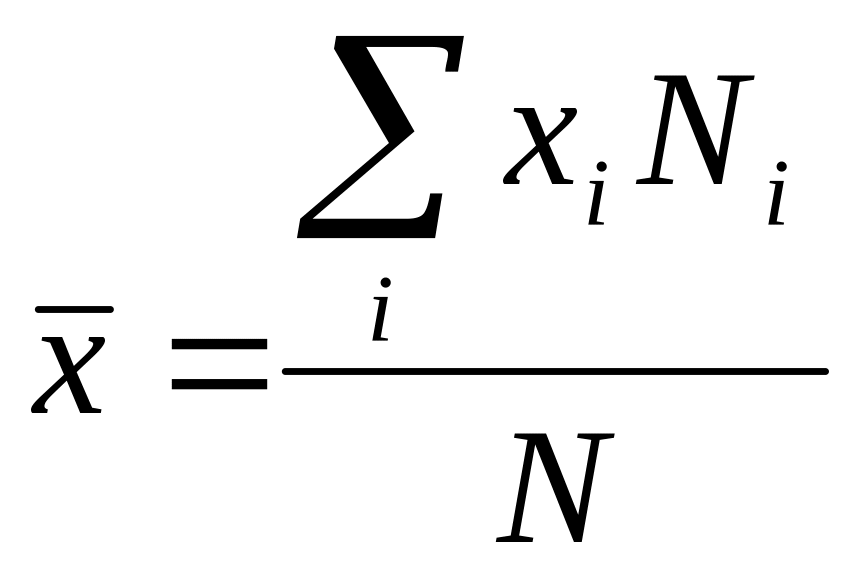стандартного отклонения
и эксцесса
;
8. Постройте гистограмму
,
взяв в качестве ширины интервала
.
9. Выбрав в качестве параметров распределения значение и , постройте в этих же координатах нормальное распределение (7).
10. Сопоставьте гистограмму и график
нормального распределения интенсивности
космического излучения (возьмите также
к вниманию значения величины
)
и сделайте выводы о возможности
аппроксимации полученных результатов
нормальным распределением.
11. Составьте таблицу, аналогичную
приведенной выше, для измерений с
интервалом времени
и повторите требования пунктов 7-10.
12. Сформулируйте выводы, которые вытекают из этих расчетов и сопоставлений.
ВНИМАНИЕ! Без предшествующей проверки приборов преподавателями или лаборантами установку не включать!
ПОМНИТЕ НА СЧЕТЧИК ПОДАЕТСЯ ВЫСОКОЕ НАПРЯЖЕНИЕ (ОКОЛО 800 ВОЛЬТ!). Во время работы экранированных проводников и контактов прибора не касаться!
Контрольные вопросы:
Является ли космическое излучение стационарным процессом?
Почему, строго говоря, этот процесс не является гауссовым?