Тема 5. Плоские однородные волны

5.1. Параметры плоской волны

5.2 Распространение волн в реальных средах

5.3 Уравнения Гельмгольца

5.1. Для описания волнового процесса вводится понятие фронт волны. Фронт волны – это геометрическое место воображаемых точек поверхности, до которых дошло возбуждение. Фронт волны иначе называют волновой фронт.

Уравнение, описывающее волновой фронт плоской волны

(5.1)

Формула (5.1) представляет собой уравнение волнового фронта плоской волны. Уравнение (5.1) показывает, что волновые фронты представляют собой бесконечные плоскости, перемещающиеся в пространстве перпендикулярно оси z.

Скорость перемещения фазового фронта называется фазовой скоростью. Фазовая скорость обозначается V_ф и определяется формулой

(5.2)

Первоначально уравнение (5.2) содержит фазу с двумя знаками – отрицательным и положительным. Отрицательный знак, т.е. , указывает, что фронт волны распространяется вдоль положительного направления распространения оси z. Такая волна называется бегущей, или падающей.

Положительный знак фазы волны указывает на движение фронта волны в обратном направлении, т.е. противоположном направлению оси z. Такая волна называется отраженной.

В дальнейшем будем рассматривать бегущие волны.

5.2 Если волна распространяется в реальной среде, то из-за происходящих тепловых потерь, неизбежно происходит уменьшение амплитуды. Рассмотрим простой пример. Пусть волна распространяется вдоль оси z и первоначальное значение амплитуды волны соответствует 100%, т.е. A₀=100. Допустим при прохождении одного метра пути амплитуда волны уменьшается на 10%. Тогда будем иметь следующие значения амплитуд волн

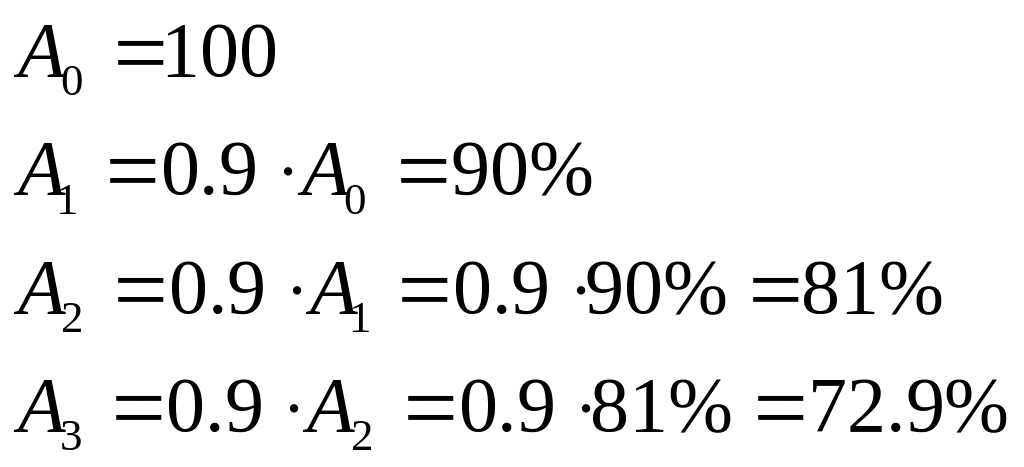
Общая закономерность изменения амплитуды имеет вид

Такими свойствами обладает показательная функция. Графически процесс можно показать в виде рис. 5.1.

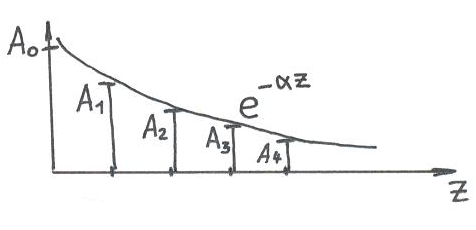
Рис. 5.1

В общем виде соотношение пропорциональности запишем как

, (5.2)

где  - постоянная затухания волны.

Фазовую постоянную  и постоянную затухания  можно объединить с помощью введения комплексной постоянной распространения , т.е.

, (5.3)

где  - фазовая постоянная,  - постоянная затухания волны.

В зависимости от вида волнового фронта различают волны плоские, сферические, цилиндрические.

Плоская волна – это волна, имеющая плоский фронт волны. Плоской волне также можно дать следующее определение. Волна называется плоской однородной, если векторное поле и в любой точке плоскости перпендикулярны направлению распространения и не изменяются по фазе и амплитуде.

Уравнение плоской волны

Если источник, порождающий волну, является точечным, то фронт волны, распространяющийся в неограниченном однородном пространстве, представляет собой сферу. Сферическая волна – это волна, имеющая сферический фронт волны. Уравнение сферической волны имеет вид

, (5.4)

где r – радиус-вектор, проведенный из начала координат, совпадающего с положением точечного источника, в конкретную точку пространства, расположенной на расстоянии r.

Волны могут возбуждаться с помощью бесконечной нити источников, расположенных вдоль оси z. В этом случае такая нить будет порождать волны, фазовый фронт которых представляет собой цилиндрическую поверхность.

Цилиндрическая волна – это волна, имеющая фазовый фронт в виде цилиндрической поверхности. Уравнение цилиндрической волны имеет вид

, (5.5)