Тема 4. Электромагнитные волны - форма существования эмп

Цель: электромагнитное поле может существовать в виде электромагнитных волн. Адекватными соотношениями, описывающими волновой характер электромагнитного поля, являются волновые уравнения - дифференциальные уравнения в частных производных второго порядка, которые могут быть получены непосредственно из уравнений Максвелла - дифференциальных уравнений в частных производных первого порядка.

4.1 Понятие волнового процесса.

4.2 Продольные и поперечные волны.

4.1 Прежде чем рассматривать волновой процесс, дадим определение колебательного движения. Колебание – это периодически повторяющийся процесс. Примеры колебательных движений весьма разнообразны: смена сезонов года, колебание сердца, дыхание, заряд на обкладках конденсатора и другие.

Уравнение колебания в общем виде записывается как

(4.1)

где - амплитуда колебаний, - циклическая частота, - время, - начальная фаза. Часто начальную фазу можно принять равной нулю.

От колебательного движения можно перейти к рассмотрению волнового движения. Волна – это процесс распространения колебаний в пространстве с течением времени. Так как колебания распространяются в пространстве с течением времени, то в уравнении волны необходимо учесть и пространственные координаты, и время. Уравнение волны имеет вид

, (4.2)

где А₀ – амплитуда,  - частота, t – время,  - волновое число, z – координата.

Физическая природа волн весьма многообразна. Известны звуковые, электромагнитные, гравитационные, акустические волны.

По типу колебаний все волны можно классифицировать на продольные и поперечные.

4.2 Продольные волны – это волны, у которых частицы среды колеблются вдоль направления распространения волны (рис. 3.1а). Примером продольной волны является звуковая волна.

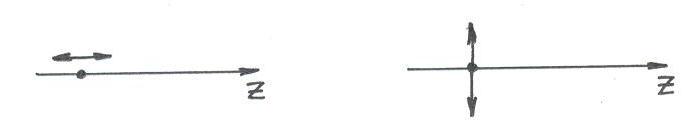
а б

Рис. 4.1

Поперечные волны – это волны, у которых частицы среды колеблются в поперечном направлении относительно направления распространения (рис. 3.1б).

Электромагнитные волны относятся к поперечным волнам. Следует учесть, что в электромагнитных волнах происходит колебание поля, и никакого колебания частиц среды не происходит. Если в пространстве происходит распространение волны с одной частотой , то такая волна называется монохроматической.

Для описания распространения волновых процессов вводятся следующие характеристики. Аргумент косинуса (см. формулу (3.2)), т.е. выражение , называется фазой волны.

Схематически распространение волны вдоль одной координаты показано на рис. 5.2, в данном случае распространение происходит вдоль оси z.

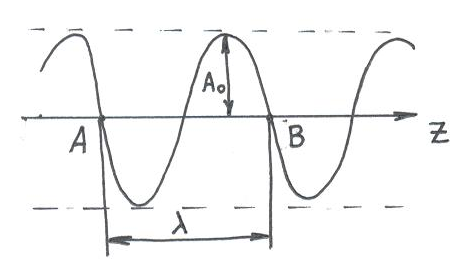
Рис. 4.2

Период – время одного полного колебания. Период обозначается буквой Т и измеряется в секундах (с). Величина обратная периоду, называется линейной частотой и обозначается f , измеряется в герцах ( =Гц). Линейная частота связана с круговой частотой. Связь выражается формулой

(4.3)

Если зафиксировать время t, то из рис. 3.2 видно, что существуют точки, например А и В, которые колеблются одинаково, т.е. в фазе (синфазно). Расстояние между ближайшими двумя точками, колеблющимися в фазе, называется длиной волны. Обозначается длина волны  и измеряется в метрах (м).

Волновое число  и длина волны  связаны между собой формулой

(4.4)

Волновое число  иначе называют фазовой постоянной или постоянной распространения. Из формулы (4.4) видно, что постоянная распространения измеряется в ( ). Физический смысл заключается в том, что она показывает, на сколько радиан изменяется фаза волны при прохождении одного метра пути.

Для описания волнового процесса вводится понятие фронт волны. Фронт волны – это геометрическое место воображаемых точек поверхности, до которых дошло возбуждение. Фронт волны иначе называют волновой фронт.