1. Содержание предмета Техническая Механика. Основные понятия. Тех. Механика – это предмет, изучающий механическое движение тел и их взаимодействие. Состоит из 3 разделов: 1.Теоретическая механика 2.Сопротивление материалов 3.Статика сооружений Теоретическая механика изучает законы механического движения и условие равновесия тел. Теоретическая механика состоит: 1.Статика 2.Кинематека 3.Динамика Статика – раздел теоретической механики, изучающий общие свойства сил и условия равновесия твердых тел, находящихся под действием приложенных к ним сил. Основные понятия статики: 1)равновесие твердого тела – такое состояние, когда тело находится в покое или движется равномерно или прямолинейно. 2)абсолютно твердое тело – тело, расстояние между точками которого не меняется при действии на него других тел (в природе таких тел нет). 3)материальная точка – точка, имеющая массу. Материальной точкой мы будем считать не только малые тела, но и тела, размерами которых в данных условиях можно пренебречь. 4)свободное тело – если никакие другие тела не препятствуют его перемещению в любом направлении. 5)сила – мера механического взаимодействия тел. Она характеризуется величиной, направлением, точкой приложения. 6)система сил – совокупность сил, действующих на данное тело. 7)Две системы сил называются эквивалентными, если одну из них можно заменить другой, не меняя при этом механического состояния свободного твердого тела. 8)Сила, эквивалентная данной системе сил, называется равнодействующей, а силы этой системы – составляющими. 9)Сила, которую уравновешивают данную систему, называют уравновешивающей. Равнодействующая и уравновешивающая силы одной и той же системы равны по модулю и действуют по одной прямой в разные стороны. Величина, которая характеризуется численным значением, линией действия, направлением и точкой приложения, называется векторной величиной, или вектором. Графически вектор изображают в виде отрезка определенной длины со стрелкой, указывающей его направление. Длина отрезка в выбранном масштабе соответствует численной величине вектора. Вектор можно характеризовать его проекциями на числовые координатные оси. Чтобы получить проекцию вектора на числовую координатную ось, нужно из точек начала и конца вектора опустить перпендикуляры на ось. Отрезок координатной оси, заключенный между двумя перпендикулярами, и будет проекцией вектора на ось. Если направление проекции от начала к концу совпадает с положительным направлением оси, то ее называют положительной, если же не совпадает, то проекцию называют отрицательной. Проекция вектора на координатную ось есть скаляр. Если для характеристики величины достаточно знать ее численное значение (положительное или отрицательное, например, температуру), то ее называют скалярной величиной, или скаляром. Представим числовую ось, т.е. прямую, на которой укажем начало отсчета (нулевую точку), нанесем масштаб и определим направление положительного (вправо) и отрицательного (влево) отсчета. Если на ось нанести скалярную величину, равную +3, то от начала отсчета на оси откладываем в положительную сторону отрезок, равный трем.

2.Аксиомы статики. Связи. Условия, при которых тело может находиться в равновесии, выводится из нескольких положений, принимаемых без доказательств, но подтвержденных опытом, называемых аксиомами статики. Первая аксиома (закон инерции) – всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения до тех пор, пока какие-нибудь силы не выведут его из этого (равновесия) состояния. Вторая аксиома (условия равновесия двух сил) – для равновесия свободного твердого тела, находящегося под действием двух сил, необходимо и достаточно, чтобы эти силы были равны по модулю, действовали по одной прямой в противоположные направления (стороны). Третья аксиома (принцип присоединения и отбрасывания уравновешенной системы сил) – равновесие твердого тела не нарушится, если к нему присоединить или удалить систему уравновешенных сил. Следствие из 2 и 3 аксиом: механическое состояние твердого тела не нарушится, если силу перенести вдоль линии ее действия. Доказательство: Пусть на твердое тело действует в числе других сил сила F, приложенная в точке А с линии действия а. В произвольной точке В приложим две уравновешенные силы 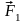и 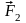, равные по модулю и противоположно направленные с │ │=│ │=│F│. Согласно второй аксиомы силы и не нарушают механического состояния тела. На основании 3 аксиомы отбросим силы F₁ и F₂, тогда оставшуюся силу F₁ можно рассматривать как силу F, перенесенную из точки А в точку В по линии действия. При этом механическое состояние не нарушается. Четвертая аксиома (правило параллелограмма сил) – равнодействующая двух сил, приложенных к телу в одной точке под углом друг к другу, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах и приложено в этой же точке. Пятая аксиома (закон равенства действия и противодействия) – силы взаимодействия между собой двух тел всегда равны по модулю и направлены по одной прямой в разные стороны. Связи. Тела, ограничивающие перемещение других тел, называется связями. Силы, действующие от связей и препятствующие перемещению, называются реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей). Связь – гладкая опора.

3. Связи. Реакции связей. Связи –это ограничения налагаемые на перемещение тел. Силы, действующие от связей и препятствующие перемещению, называются реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей). Идеальная связь – связь без трения. При решении задач статики пользуются принципом освобождаемости от связей: всякое несвободное тело можно считать свободным отбросив все связи и заменив их реакциями.

Правило направления реакций: реакции всегда направлены в сторону противоположную тому направлению, куда связь мешает перемещению тела.

Виды связей и их реакции:

1.Идеальная – гладкая поверхность

2.идеально-гладкая нить или стержень

3.идеально-гладкий цилиндрический шарнир( шарнирно-неподвижная опора)

4.шарнирно-подвижная опора

5.защемление

4. Плоская система сходящихся сил. Графический и геометрический способ. Плоская система сходящихся сил - это сист. сил при которой линии действия, которых лежат в одной плоскости и пересекаются в одной точке

Теорема о П.С.С.С.: П.С.С.С.в общем случае эквивалентна равнодействующей силе которая равна векторной сумме сост сил и проходит через точку их пересечения.

Равнодействующую можно определить 3 способами:1.аналитический; 2.графический; 3.геометрический

Графический способ опред равнодействующей П.С.С.С.: графический способ заключ в построении силового многоугольника в строгом масштабе. Для численного опред равнодействующей измеряют, вектор R b умножают на масштаб.

Геометрический способ опред равнодействующей: =

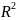Cos(180-α)= - cos α; R=

По теореме синусов:

Геометрическое усл равновесия П.С.С.С.: если при построении силового многоугольника он замыкается, это значит, что равнодействующая =0

5. Аналитический способ определения равнодействующей плоской системы сходящихся сил. Условия равновесия системы сходящихся сил. Пусть имеем систему сходящихся сил в точке А, где R – равнодействующая этой системы, полученная графическим методом.

У F2 F3 ,

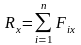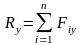
F1

Ry Fn ,

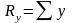
R

Rx x

Из математики известны, что проекции равнодействующей на ось равна алгебраической сумме проекции сил составляющих на эту ось.

Модуль равнодействующей.

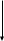Y R

R_y=Σy

R_x=Σx x

, ; , .

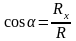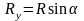Аналитическое условие равновесия плоской системы сходящихся сил. Если плоская система сил находится в равновесии, то равнодействующая такой системы равна 0 (R=0). Значит и проекции равнодействующей равны 0 (Rx=0, Ry=0). Rx=0, Σx=0; Ry=0, Σy=0 – аналитическое условие равновесия. Для аналитического условия равновесия необходимо и достаточно, чтобы проекции сил на ось х и на ось y равнялись 0.

Методика решения задач определения равнодействующей аналитическим способом. 1)Выбираем точку равновесия, которое нужно рассмотреть. 2)отбрасываем связи и заменяем их реакциями. 3)придерживаясь некоторого масштаба, делят четкий схематический чертеж с изображением активных сил и реакции связей. 4)выбираем систему координат. За начало координат удобно принять точку пересечения линий действия неизвестных сил. Одну из осей нужно направлять по одной из неизвестных сил, т.к. в этом случае она будет проектироваться в точку. 5)составляем уравнение равновесия Σy=0, Σx=0, из которых определяют искомые реакции

6. Теорема о равновесии трёх непараллельных сил. Проекции силы на оси координат. Проекции сил на оси координат:

1.если сила перпендикулярна оси, то её проекции на эту ось равна нулю

2.если сила лежит, параллельна оси или лежит на оси, то её проекция на эту ось равна самой силе

Правило знаков проекции: если направление силы совпадает с положительным направлением оси, то её проекция берётся со знаком плюс, не совпадает- с минусом

Теорема о трех силах: Если приложенные к твердому телу 3 непараллельные силы, лежащие в одной плоскости, находятся в равновесии, то линии их действия пересекаются в одной точке. Доказательство: Тело находится в равновесии под действием , , 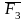. В приложенных точках АВС найдем равнодействующую сил и по правилу параллелограмма. Согласно 2-ой аксиоме для равновесия необходимо и достаточно, чтобы сила была уравновешивающей или R. Это возможно в том случае, когда и R лежат на одной прямой и имеют противоположное направление, то тогда линии действия , , пересекутся в одной точке О

Проекции сил на оси координат. В тех случаях, когда на тело действует более трех сил, а также когда не известны направления некоторых сил при решении задач пользуются не геометрическим, а аналитическим уровнем равновесия, который основан на методе проекций.

Проекция силы на ось – отрезок оси, заключенный между перпендикулярными опущенными на ось из начала и конца вектора силы.

7. Геометрическое и аналитическое условие равновесия плоской системы сходящихся сил. Геометрическое усл равновесия П.С.С.С.: если при построении силового многоугольника он замыкается, это значит, что равнодействующая =0

Аналитическое усл равновесия П.С.С.С.: для равновесия сист сходящихся сил необходимо и достаточно что бы алгебраическая сумма проекций всех сил на оси координат равнялась нулю.

8. Пара сил, момент пары, эквивалентность пары. Условие равновесия плоской системы пар сил. Пара сил – это система двух параллельных сил, приложенных к одному твердому телу, равных по модулю и противоположно направленных.

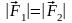, (F1;-F2), 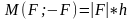(кН*м). Плечо пары Н – кратчайшее расстояние между линиями действия сил пары. Эффект действия пары вращения. Вращательное действие характеризуется моментом. Момент пары – величина, равная произведению модуля одной из сил, составляющих пару на ее плечо, взятая со знаком «+» или «-». Знак момента определяется по правилу: если пара стремится повернуть тело в сторону часовой стрелки, то выражение момента берем знак «+», если против часовой стрелки, то «-». Эквивалентность пар. Две пары считаются эквивалентными, если после замены одной пары другой механическое состояние тела не изменится, т.е. не изменится движение тела или не нарушится его равновесие. Примем следующие свойства сил без доказательств: действие пары на тело не изменит механического состояния тела, если пару повернуть на любой угол в плоскости ее действия или переместить как угодно в плоскости ее действия, сохраняя при этом знак момента. Не изменяя механического состояния тела можно менять модуль сил и плечо пары, но при условии, чтобы ее момент и направление вращения оставались неизменными. Условно момент обозначают следующими символами:

Свойства пары: 1)момент пары сил не меняется, если перенести силы вдоль линий их действия, т.к. при этом плечо остается постоянным. 2)пара сил не может быть приведена к равнодействующей и не может быть уравновешена одной силой. 3)алгебраическая сумма проекции сил пары на любую ось равна нулю. 4) алгебраическая сумма моментов сил составляющих пару относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары. Доказательство: Дана пара F1-F2 с плечом h и моментом m=-F1*h=-F2*h.

M_A(F1)=F1*a, M_A(F2)=-F2*(h-a), M_A(F1)+ M_A(F2)=F1a-F2h-F2a=-F2h.

Условие равновесия: для равновесия плоской сист пар сил необходимо и достаточно что бы алгебраическая сумма моментов сост.пар равнялась нулю

Условия равновесия плоской системы пар сил. Пары подобно силам можно складывать и разлагать. Пара, заменяющая собой действие данных пар, называется равнодействующей, а пары данные, ее составляющими. Примем без доказательства теорему сложения пар: Система пар сил, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов, составляющих пар, т.е.

M(R;-R)=m(F1;-F1)+m(F2;-F2)+…+m(Fn;-Fn)= 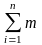(Fi;-Fi)=Σm_i.

Из теоремы сложения пар сил, лежащих в одной плоскости. Плоская система пар сил находится в равновесии, если алгебраическая сумма момента этих пар равна 0.

9. Момент силы относительно точки – это произведение модуля силы на ее плечо.

М₀(F)=│F│*h

Центр момента – точка, относительно которой берется момент. Плечо силы относительно точки – кратчайшее расстояние от точки до линии действия силы. Момент силы относительно точки равен нулю, если точка лежит на линии действия силы, т.к. плечо равно 0. Момент силы не изменится, если силу перенести вдоль линии ее действия.

Теорема о параллельном переносе сил: Механическое состояние твердого тела не нарушится, если данную силу перенести параллельно самой себе в произвольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложения. Доказательство: Возьмем тела, находящиеся под действием системы сил, в числе которых сила F приложена в точке А. Выберем параллельную точку О, которую назовем центром приведения и на основании 3 аксиомы приложим в этой точке 2 равные силы F1 и F2, параллельные данной силе, причем F = F1= F2. Систему сил (F; F1; F2), эквивалентную силе F представим как силу F, перенесенную параллельно самой себе в произвольно выбранный центр приведения О и пару сил (F1– F2), момент которой равен моменту данной силы относительно центра приведения О, являющейся новой точкой приложения силы F: m(F1;-F2)=F*h=M₀/F

Теорема Вариньона, теорема механики, устанавливающая зависимость между моментами сил данной системы и моментом их равнодействующей. 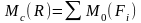. Согласно теореме Вариньона, если система сил Fi имеет равнодействующую R, то момент Мо (Fi) равнодействующей относительно любого центра О (или оси z) равен сумме моментов Mo (Fi) составляющих сил относительно того же центра О (или той же оси z).

Данной теоремой пользуются при решении ряда задач механики (особенно статики), сопротивления материалов, теории сооружений и др

10. Теорема о параллельном переносе сил.

Теорема о параллельном переносе сил: Механическое состояние тела не нарушается, если силу перенести параллельно самой себе в любую точку плоскости, добавив при этом пару, момент которой равен моменту данной силы относительно новой.

11. Приведение плоской системы произвольно расположенных сил к данному центру. Главный вектор и главный момент. В общем случае произвольно расположенная система сил приводится к главному вектору (для системы пар сил находят эту равнодействующую. Главный вектор равен векторной сумме составляющих сил) и к главному моменту (для системы пар сил можно найти одну равнодействующую пару, момент которой равен алгебраической сумме моментов составляющих сил относительно новой точки приложения). Для равновесия такой системы сил необходимо и достаточно 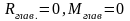. Главный вектор можно определить и в аналитической форме через проекции на координатные оси всех действующих сил 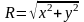Для того чтобы 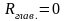необходимо, чтобы и проекции его на оси равнялись 0: 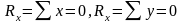. Кроме того, и 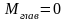, т.е. алгебраическая сумма моментов всех сил равна 0. Таким образом, получим три уравнения равновесия произвольной плоской системы сил в аналитической форме: 1. . Следовательно, для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекции всех сил на оси координат равнялась 0 и алгебраическая сумма моментов всех сил относительно любой точки плоскости равнялась 0. Эта форма уравнений равновесия называется первой или основной. Существуют еще две формы. 2. . Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы порознь равнялось 0 алгебраическая сумма моментов всех сил относительно каких-либо двух точек, и сумма проекции сил на любую ось не перпендикулярную прямой проходящей через эти две точки. 3. . 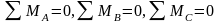Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы равнялись 0 алгебраические суммы момента всех сил относительно любых трех точек плоскости, не лежащих на одной прямой.

12. Аналитическое условие равновесия плоской системы произвольно расположенных и параллельно направленных сил. Условие равновесия плоской системы параллельных сил. Система параллельных сил является частным случает произвольной системы, поэтому должно удовлетворять уравнением ее равенства в основной форме. Направим ось у параллельно силам Ах перпендикулярно салам, видно что проекция силы на ось х равна нулю, поэтому уравнение сумма всех сил на ось х 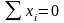удовлетворяется не зависимо от того будет ли эта система в равновесии или нет и не может служить в качестве уравнения равновесия. Таким образом, для равновесия системы параллельных сил остаются два уравнения 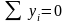, 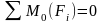. Итак, для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись 0, алгебраическая сумма моментов всех сил относительно любой точки плоскости и алгебраическая сумма проекции всех сил на ось, параллельную силам. Эти уравнения равновесия могут быть представлены и в другой форме . 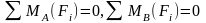То есть для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы равнялась 0 алгебраическая сумма моментов всех сил относительно двух точек.

13. Балка, виды опор балок и определение их реакций. Балка – конструктивный элемент, у которого длина значительно превышает размеры поперечного сечения. Виды опор балок: 1. Шарнирно неподвижная. 2. Шарнирно подвижная. 3. Защемление. Виды однопролётных балок: 1. Бесконсольная на двух опорах 2. Одноконсольная на двух опорах 3. Двухконсольная на опорах 4. Балка – консоль. Балка с защемлением.