6.1.1.5. Хвильові властивості мікрочастинок. Хвилі де Бройля

Французький вчений де Бройль висунув гіпотезу (1924 р.) про універсальність корпускулярно–хвильового дуалізму, тобто твердження, що не тільки електромагнітне випромінювання являє собою хвильовий процес і потік частинок (квантів випромінювання, фотонів) одночасно, але й мікрочастинки аналогічно зв’язані з хвильовим процесом. Якщо частинка має енергію ε та імпульс Р, то з нею пов’язується хвиля з частотою:

(6.1.12)

та довжиною хвилі

або . (6.1.13)

Ця хвиля називається хвилею де Бройля. Хвильова природа мікрочастинок виявлена експериментально (дифракція електронних та нейтронних пучків на кристалах). Хвильові властивості електронних пучків використовуються в роботі електронного мікроскопа. Довжина хвилі де Бройля для електронів значно менша довжини світлової хвилі, що обумовлює дуже велику роздільну здатність електронного мікроскопа, що дає можливість одержати інформацію про окремі атоми і молекули речовини, що неможливо отримати за допомогою оптичного мікроскопа.

6.1.1.6. Елементи релятивістської динаміки

В модулі «механіка» було сформульовано постулати спеціальної теорії відносності Ейнштейна, та основні висновки з них (див. розд. 1.1.2.3). Тепер розглянемо основні поняття релятивістської динаміки, що тісно зв’язані з поняттями про кванти, енергію елементарних частинок.

Залежність маси від швидкості (релятивістська маса):

чи , (6.1.14)

де – маса спокою частинки; – її швидкість; – швидкість світла в вакуумі; – швидкість частинки, яка виражена в долях від швидкості світла ( ).

Якщо тіло не рухається, то його енергія дорівнює енергії спокою:

E₀=m₀c². (6.1.15)

Енергію спокою матиме будь-який матеріальний об’єкт, що характеризується масою. Енергії спокою не мають ті частинки, що існують тільки в русі зі швидкістю світла, наприклад фотони.

Взаємозв’язок маси та енергії релятивістської частинки:

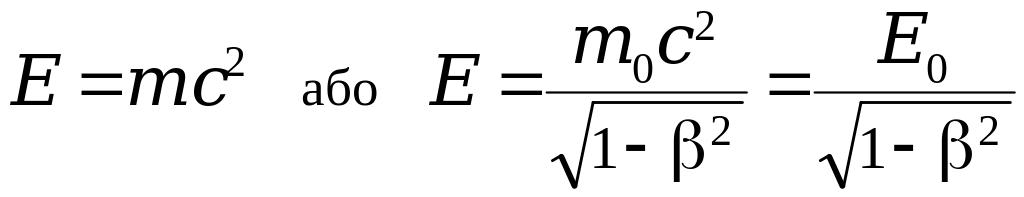, (6.1.16)

де E₀=m₀c² – енергія спокою частинки.

При збільшенні енергії системи на довільну величину маса системи зростає на величину ₀/с².

Повна енергія вільної частинки:

,

де T – кінетична енергія релятивістської частинки.

Кінетична енергія релятивістської частинки:

. (6.1.17)

Імпульс релятивістської частинки:

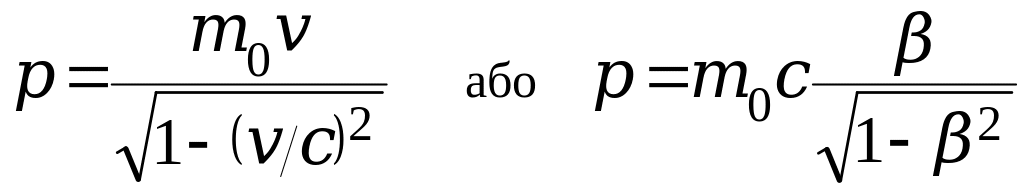. (6.1.18)

Зв’язок між повною енергією та імпульсом релятивістської частинки:

. (6.1.19)

Таким чином, можна зробити висновок, що імпульс частинки зв’язаний з кінетичною енергією T:

а) якщо швидкість частинки значно менша за швидкість світла << c , то:

;

б) якщо швидкість частинки зрівняна зі швидкістю світла (релятивістський випадок), то:

, (6.1.20)

де m₀ – маса спокою частинки; m – релятивістська маса; – швидкість частинки; c – швидкість світла у вакуумі; E₀ – енергія спокою частинки ( E₀=m₀c² ).

Співвідношення невизначеностей

(короткі тези матеріалу для виступу на студентській конференції)

а) для координати та імпульсу,

де − невизначеність проекції імпульсу на вісь x;

– невизначеність координати;

б) для енергії та часу,

де – невизначеність енергії; – час життя квантової системи в даному енергетичному стані.

Одновимірне рівняння Шредінгера для стаціонарних станів:

, (6.1.1.21)

де – хвильова функція, яка описує стан частинки; m – маса частинки; E – повна енергія; U(x) – потенціальна енергія частинки.

Густина ймовірності:

де – ймовірність того, що частинка може бути знайдена поблизу точки з координатою x на ділянці dx.

Ймовірність знаходження частинки в інтервалі від x₁ до x₂ :

.

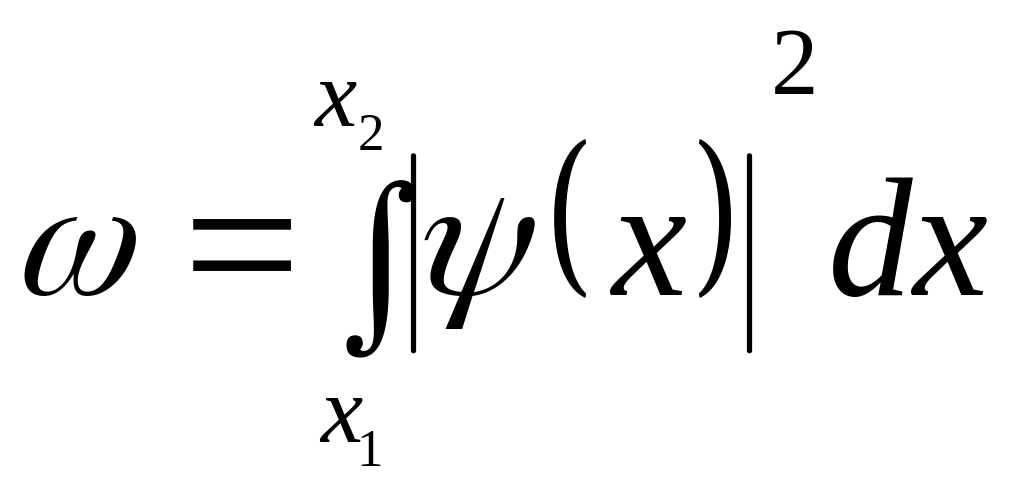Розв’язок рівняння Шредінгера для одномірної, нескінченно глибокої, прямокутної потенціальної ями:

а) – власні нормовані хвильові функції;

б) – власні значення енергії,

де n – квантове число (n=1,2,3...); l – ширина потенціальної ями.

При цьому в області .