МОДУЛЬ 4. «ЕЛЕКТРОМАГНЕТИЗМ. ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ ТА ХВИЛІ»

4.1. ОСНОВИ ТЕОРІЇ

4.1.1. Магнітне поле

4.1.1.1. Індукція магнітного поля

Силовою характеристикою магнітного поля є векторна фізична величина – магнітна індукція .

Напрямок вектора магнітної індукції встановлюється за результатом дії магнітного поля на: 1) провідник зі струмом; 2) магнітну стрілку; 3) заряджену частинку, що рухається в магнітному полі; 4) рамку зі струмом.

За напрямок вектора у даній точці магнітного поля приймається напрямок, вздовж якого розташовується позитивна нормаль вільної рамки зі струмом, вміщеної у цю точку поля. В цьому ж напрямку вказує і північний полюс магнітної стрілки, вміщеної в цю точку поля.

Напрямок позитивної нормалі рамки зв’язаний з напрямком струму правилом правого гвинта (правилом свердлика): якщо обертальний рух головки гвинта збігається з напрямком струму в рамці, то поступальний рух вістря вказує напрямок нормалі , отже напрямок вектора магнітної індукції , що проходить через дану точку поля. Вектор у даній точці збігається з дотичною в цій точці до лінії магнітної індукції. Магнітне поле є вихровим, його силові лінії замкнені.

Модуль вектора магнітної індукції в будь-якій точці поля визначається максимальним обертальним моментом, який діє з боку поля на рамку, по якій протікає одинична сила струму, з одиничною площею поверхні, коли нормаль рамки перпендикулярна до напрямку ліній магнітного поля:

. (4.1.1)

Одиниця магнітної індукції – тесла (Тл). =1 кг с ^-2 А ^-1 .

Магнітна індукція зв’язана з напруженістю магнітного поля, що є аналогом розглянутої нами в попередньому розділі (модуль 3, ч.1 посібника) силової характеристики електричного поля - напруженості електричного поля :

, (4.1.2)

де – магнітна проникність ізотропного середовища; – магнітна стала. Про величину та її значення буде сказано далі; аналогічна величина – електрична стала була розглянута нами при записі закону Кулона в системі СІ (так звана раціоналізація системи одиниць СІ).

Для вакууму (по визначенню поняття магнітної проникності середовища), тому магнітна індукція у вакуумі дорівнює:

.

Напруженість магнітного поля не залежить від магнітних властивостей середовища.

Джерелом магнітного поля є електричний струм (струм провідності, струм зміщення, або окремий рухомий електричний заряд. За своєю природою магнітне поле вихрове: його силові лінії замкнуті і завжди охоплюють провідник зі струмом. Характер поля (вихрове чи потенціальне) визначається циркуляцією вектора відповідного поля.

Циркуляцією вектора поля називають криволінійний інтеграл по замкненому контуру від скалярного добутку вектора поля на нескінченно малий елемент довжини контуру.

Отже, за визначенням циркуляція вектора напруженості магнітного поля запишеться у вигляді:

,

де – проекція вектора на ; – замкнений контур, вздовж якого обчислюється циркуляція.

Якщо циркуляція вектора поля по довільному замкненому контуру дорівнює нулю, то поле називається потенціальним (наприклад, гравітаційне поле, електростатичне); для вихрового поля (магнітного) циркуляція відмінна від нуля.

В основу сучасних методів розрахунку магнітних полів постійних струмів покладена теорема про циркуляцію вектора напруженості , яка ще називається законом повного струму. Для таких магнітних полів, як поле соленоїда, тороїда, прямолінійного струму, цей закон дозволяє розрахувати напруженість без застосування закону Біо – Савара - Лапласа (див. далі).

Закон повного струму: циркуляція вектора напруженості магнітного поля по довільному замкненому контуру дорівнює алгебраїчній сумі струмів, охоплених цим контуром:

,

де – число струмів, охоплених контуром.

Принцип суперпозиції. З досліду витікає, що в будь–якій точці магнітного поля, створеного замкненим провідником зі струмом довільної форми, магнітна індукція залежить від форми провідника. Це означає, що в будь–якій точці поля магнітна індукція створюється кожною ділянкою цього провідника, тобто для магнітних полів виконується принцип суперпозиції:

. (4.1.3)

Вектор магнітної індукції у будь – якій точці магнітного поля, створеного замкненим провідником зі струмом довільної форми, являє собою векторну суму індукцій полів, створених у цій точці кожною окремою нескінченно малою ділянкою даного провідника зі струмом. Знаходження суми нескінченно великої кількості таких з точки зори математики і є знаходження значення інтеграла вздовж кривої, що створена замкненим провідником зі струмом довільної форми (так званий криволінійний інтеграл). Таке інтегрування є порівняно простою математичною задачею тільки для деяких конкретних випадків – наприклад, проходження струму по прямолінійних відрізках провідника, по коловому провіднику (кільце зі струмом).

4.1.1.2. Закон Біо – Савара – Лапласа

Цей закон визначає вектор магнітної індукції , створений окремим нескінченно малим елементом замкненого провідника зі струмом І у довільній точці. Величина вектора магнітної індукції , тобто його модуль, згідно цього закону дорівнює:

. (4.1.4)

З акон Біо – Савара – Лапласа, таким чином, можна сформулювати так: магнітна індукція , створена елементом довільного замкненого провідника зі струмом, прямо пропорційна силі струму в провіднику І, довжині елемента провідника , обернено пропорційна квадрату відстані від елемента до точки спостерігання і залежить від орієнтації цього елемента в просторі.

Положення точки, в якій визначається магнітна індукція , однозначно визначається радіус – вектором - його напрямком та величиною (тобто модулем радіус – вектора ). Напрямок вектора визначається за правилом правого гвинта. Вектор перпендикулярний до площини, в якій лежать вектори і (рис. 4.1.1).

У більш загальній, векторній формі запису, використовуючи поняття векторного добутку, цей закон можна записати так:

. (4.1.5)

З визначення векторного добутку двох векторів напрямок вектора буде перпендикулярним до площини, в якій лежать вектори і , і визначається за правилом правого гвинта.

Використання цього закону дозволило розрахувати магнітну індукцію магнітних полів у багатьох конкретних випадках, таких, як поле в центрі та на осі колового струму, поля прямого провідника зі струмом тощо.

Так, магнітна індукція в центрі колового струму:

, (4.1.6)

де – радіус колового витка зі струмом.

Магнітна індукція на осі колового струму:

, (4.1.7)

де – відстань від центра витка до точки, в якій визначається магнітна індукція.

Магнітна індукція поля створеного нескінченним прямолінійним провідником зі струмом:

, (4.1.8)

де – відстань від осі провідника до точки, в якій визначається магнітна індукція.

Магнітна індукція поля соленоїда (котушки):

, (4.1.9)

де n – число витків на одиницю довжини соленоїда ( у СІ – в 1/м).

Магнітна індукція поля, що створюється відрізком провідника зі струмом (рис. 4.1.2, а ).

. (4.1.10)

Тут напрямок вектора магнітної індукції позначено крапкою. Це означає, що вектор направлений перпендикулярно до площини рисунка (в напрямку “на нас”). У випадку, коли вектор направлений перпендикулярно до площини рисунка, але в напрямку „від нас”, вектор позначаємо .

При симетричному розташуванні кінців провідника відносно точки, в якій визначається магнітна індукція (рис 4.1.2,б) будемо мати:

.

Тоді:

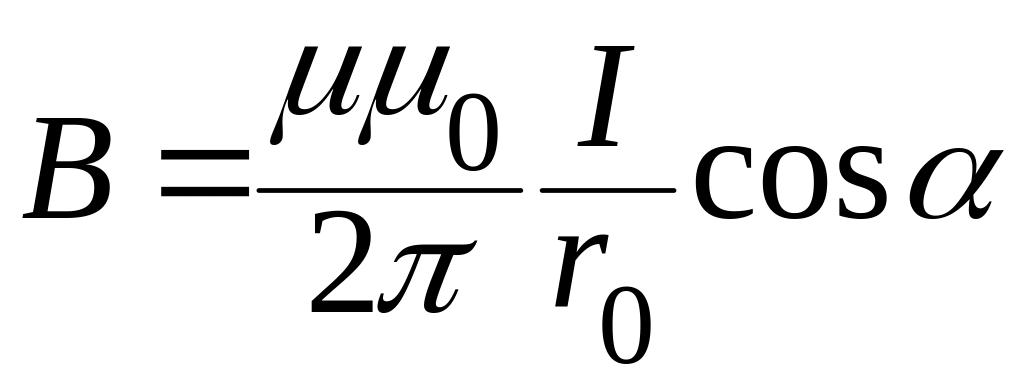. (4.1.11)

4.1.1.3. Сила Ампера

Сила Ампера – це сила, що діє з боку магнітного поля на відрізок замкненого провідника зі струмом І, що поміщений у магнітне поле. Величина сили Ампера визначається (закон Ампера) так:

, (4.1.12)

де – довжина провідника; - кут між напрямком струму в провіднику та вектором магнітної індукції . Цей вираз дійсний для однорідного магнітного поля та прямого відрізка провідника. Напрямок сили Ампера визначається за правилом лівої руки, яке є наслідком правила векторного добутку (рис. 4.1.3).

Визначити індукцію магнітного поля В у будь-якій точці можна, використовуючи закон Ампера, аналогічно (4.1.1):

. (4.1.13)

У випадку, коли поле неоднорідне і провідник не є прямим, то закон Ампера можна застосувати до нескінченно малого елемента провідника окремо:

, (4.1.14)

або

, (4.1.15)

де α – кут між вектором і ; напрямок вектора збігається з напрямком струму І в провіднику, а його модулем є нескінченно мала довжина провідника: .