- •Содержание.
- •2.3 Расчёт объёмно-поверхностных характеристик ла 7
- •Проектные данные и задание на проект:
- •1 Назначение и требования к проектируемому ла
- •1.1 Назначение ла (Цель)
- •1.2 Требования к ла
- •2 Расчёт объёмно-поверхностных характеристик ла
- •2.1 Определение размеров ла
- •2.2 Расчёт объёмно-поверхностных характеристик составляющих элементов
- •2.3 Расчёт объёмно-поверхностных характеристик ла
- •2.4 Расчет коэффициента заполнения
- •3 Определение аэродинамических характеристик ла
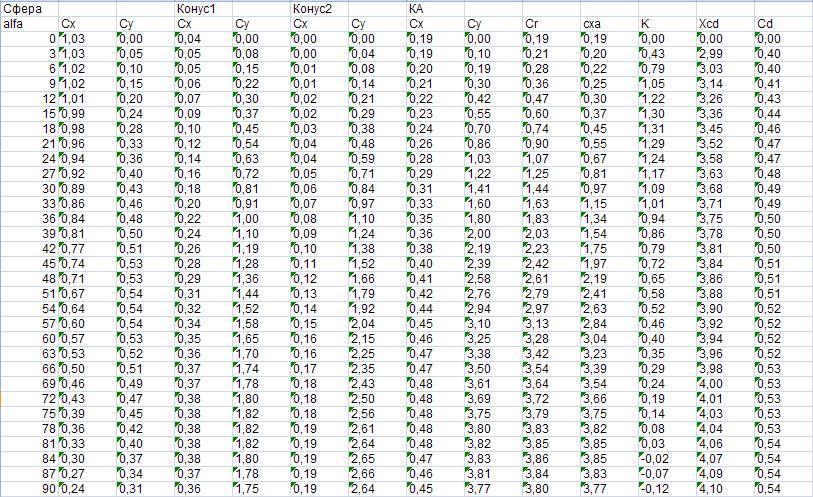
- •3.1 Определение аэродинамических характеристик составных частей
- •Определение аэродинамических характеристик усечённого конуса 1.
- •3.2 Определение аэродинамических характеристик ла в связанной системе координат
- •3.3 Определение характеристик ла в скоростной системе координат
- •3.3 Определение аэродинамического качества
- •3.4 Определение центра давления ла.
- •3.5 Определение центра масс летательного аппарата.
- •4 Массовая сводка
- •5 Тепловой режим спуска
- •5.1 Баллистика спуска
- •5.2 Определение числа Рейнольдса
- •5.3 Определение теплового потока
5 Тепловой режим спуска
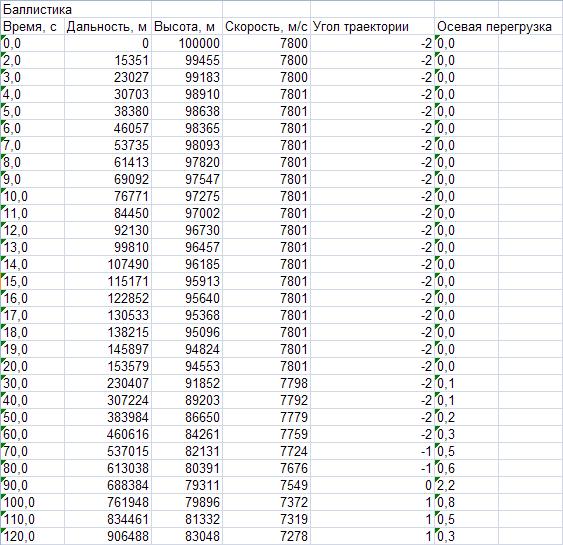
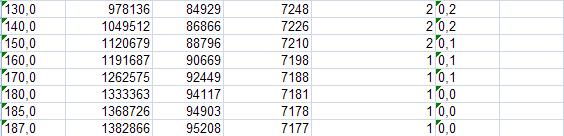
5.1 Баллистика спуска
Запишем систему уравнений движения тела сосредоточенной массы, т.е. без учёта моментов инерции. Примем, что движение происходит в однородном плоскопараллельном поле сил тяготения и в стандартной атмосфере. Тогда:

где сила лобового сопротивления Xa и подъёмная сила Ya:
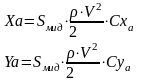
Тогда, после упрощения, окончательно получим:

Решение этой системы будем производить
методом Рунге-Кутта с шагом
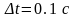 .
.
Данные стандартной атмосферы берутся из таблицы временной стандартной атмосферы ВСА-60. Данные этой таблицы изобразим графически:

Рис. 12

Рис. 13
Управление ЛА при спуске будем осуществлять с помощью изменения угла крена.
Изобразим графически результаты решения для системы уравнений спуска ЛА в атмосферу Земли.
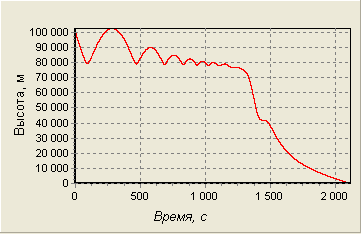
Рис. 14
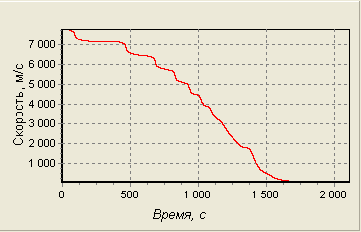
Рис. 15
5.2 Определение числа Рейнольдса
При входе ЛА в атмосферу Земли с гиперзвуковой скоростью его поверхность подвергается интенсивному нагреву, величина которого определяется скоростью набегающего потока, плотностью атмосферы и формой аппарата.
Снижение скорости ЛА за счёт тормозящего действия плотных слоёв атмосферы. Кинетическая энергия летящего тела переходит в тепловую энергию набегающего воздушного потока, обтекающего тело. Подавляющая часть выделяющейся энергии рассеивается по траектории движения аппарата, и только 3…5% передаётся ЛА.
Критерием, оценивающем переход от ламинарного течения в пограничном слое к турбулентному обтеканию аппарата, является критерий Рейнольдса.
За значение числа Рейнольдса, определяющее
границу режимов обтекания, принято
 ,
т.е течение больше порогового соответствует
турбулентному течению, а меньше
ламинарному.
,
т.е течение больше порогового соответствует
турбулентному течению, а меньше
ламинарному.
Число Рейнольдса определяется соотношением:
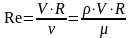 ,
,
где
R – характерный размер
(для сферы затупления носовой части ЛА
примем радиус сферы),
- плотность атмосферы, μ – коэффициент
динамической вязкости, –
коэффициент кинематической вязкости,
V – скорость ЛА.
–
коэффициент кинематической вязкости,
V – скорость ЛА.
Для траектории спуска нашего ЛА изменение числа Рейнольдса покажем графически:
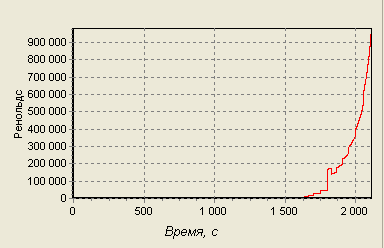
Рис. 16
5.3 Определение теплового потока
Рассмотрим область носового заведения.
Для ламинарного режима обтекания
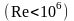 :
:

где
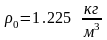 -
плотность атмосферы у поверхности
Земли,
-
плотность атмосферы у поверхности
Земли,
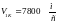 - первая космическая скорость.
- первая космическая скорость.
Для турбулентного слоя
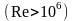 :
:

Для радиационного теплового потока:

Изобразим графически изменение тепловых потоков по времени полёта.
Предполагая, что в течение всего спуска течение ламинарное, получим:
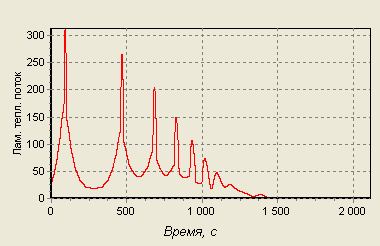
Рис. 17
Предполагая, что в течение всего спуска течение турбулентно, получим:
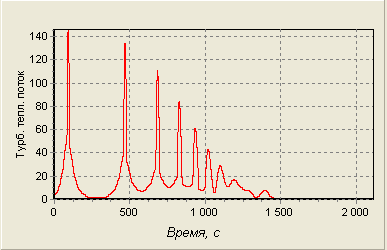
Рис. 18
Радиационный тепловой поток:
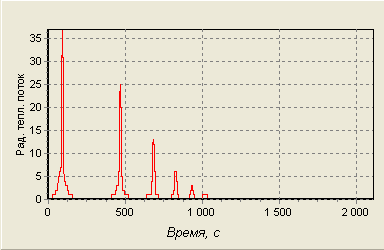
Рис. 19
Учитывая, что режим обтекания зависит от числа Рейнольдса, получим:
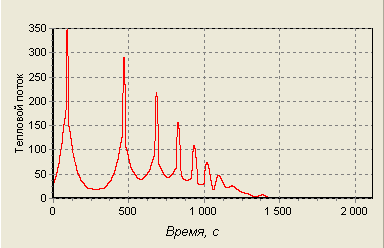
Рис. 20
Суммарный тепловой поток.
Для ламинарного течения:
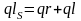
Для турбулентного течения

В силу малости радиационного потока, по сравнению с другими, им можно пренебречь.
Тогда изобразим на одном графике ql, qt и q:
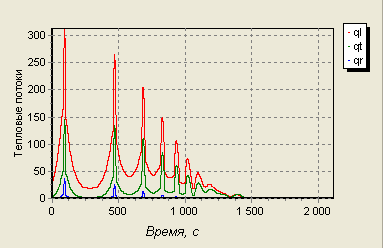
Рис. 21
5.4 Температура поверхности
Для ламинарного течения:

где
 - коэффициент черноты
- коэффициент черноты
 ,
,
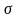 - постоянная Стефана-Больцмана
- постоянная Стефана-Больцмана
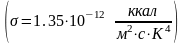
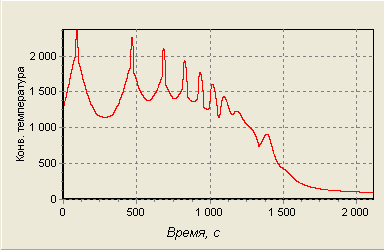
Рис. 22
Для турбулентного течения:
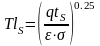
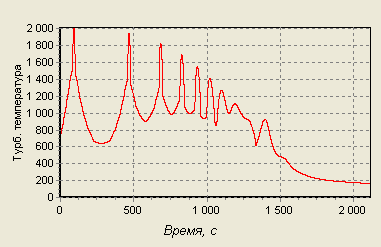
Рис. 23
Учитывая зависимость режима обтекания от числа Рейнольдса, получим:
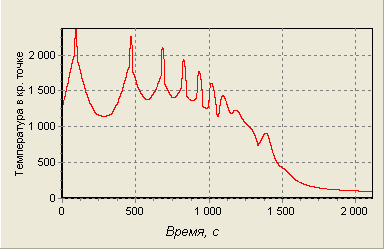
Рис. 24
Результаты расчётов сведём в таблицу – приложение № 6.
6 Определение моментов инерции по объёму и по поверхности
6.1 Сферический сегмент
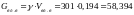 кг
кг

Координаты центра масс:

Моменты инерции по объёму сферического сегмента.
Относительно плоскостей:

Относительно осей:

Относительно центра тяжести по объёму сферического сегмента:

Момент инерции по площади сферического сегмента.
Относительно плоскостей:

Относительно осей:
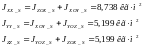
Относительно центра тяжести по площади поверхности сферического сегмента:

6.2 Усечённый конус 1
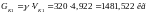


Координаты центра масс.

Моменты инерции по объёму усечённого конуса 1.
Относительно плоскостей:

Относительно осей:

Относительно центра тяжести по объёму усечённого конуса 1:
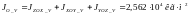
Момент инерции по площади усечённого конуса 1.
Относительно плоскостей:

Относительно осей:

Относительно центра тяжести по площади поверхности усечённого конуса 1:

6.2 Усечённый конус 2

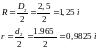

Координаты центра масс.

Моменты инерции по объёму усечённого конуса 2.
Относительно плоскостей:

Относительно осей:
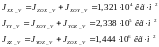
Относительно центра тяжести по объёму усечённого конуса 2:

Момент инерции по площади усечённого конуса 2.
Относительно плоскостей:

Относительно осей:

Относительно центра тяжести по площади поверхности усечённого конуса 2:
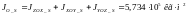
6.3 Момент инерции ЛА
Момент инерции по объёму ЛА.
Относительно плоскостей:
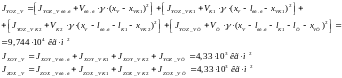
Относительно осей:

Относительно центра тяжести по объёму усечённого конуса 2:

Момент инерции по площади ЛА.
Относительно плоскостей:

Относительно осей:

Относительно центра тяжести по площади поверхности усечённого конуса 2:

Приложение
Приложение № 1. Теоретический чертёж.
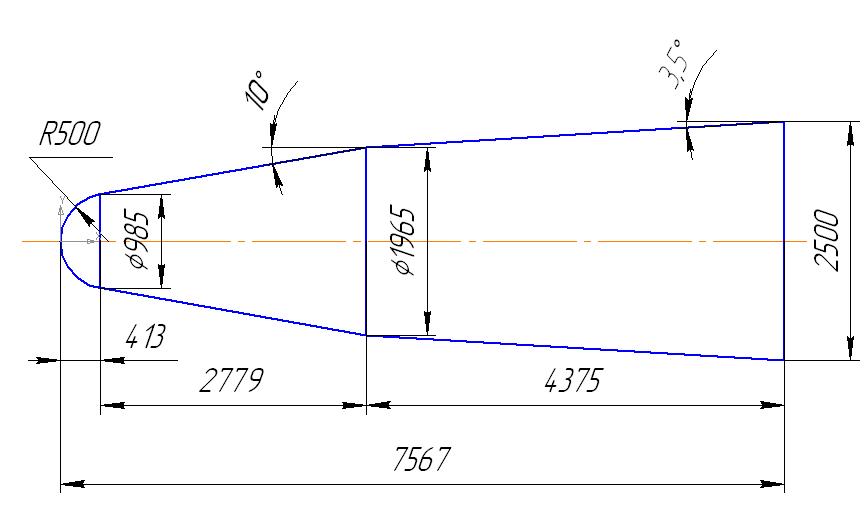 Приложение
№ 2. Объёмно-поверхностные характеристики.
Приложение
№ 2. Объёмно-поверхностные характеристики.
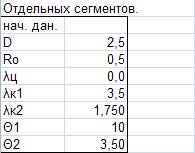
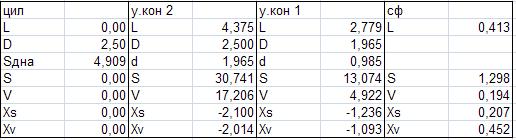
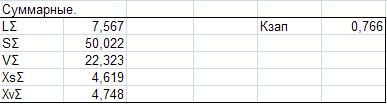
 Приложение
№ 3. Аэродинамические характеристики.
Приложение
№ 3. Аэродинамические характеристики.
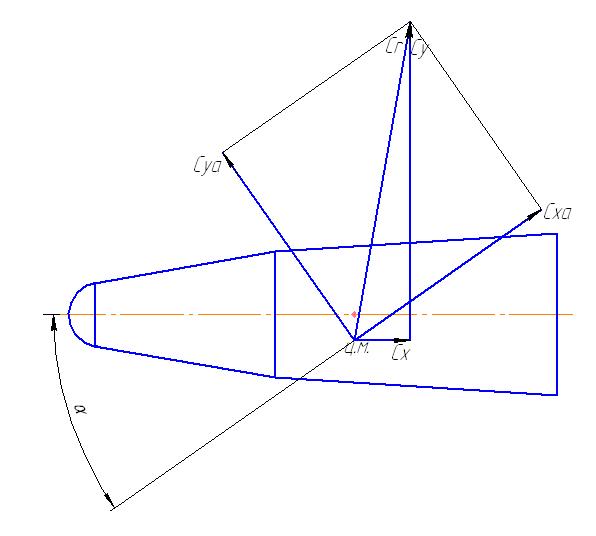
 Приложение
№ 4. Схема действия аэродинамических
сил.
Приложение
№ 4. Схема действия аэродинамических
сил.
 Приложение
№ 6. Баллистика и тепловой расчёт.
Приложение
№ 6. Баллистика и тепловой расчёт.