Модели парной регрессии

Линейная функция

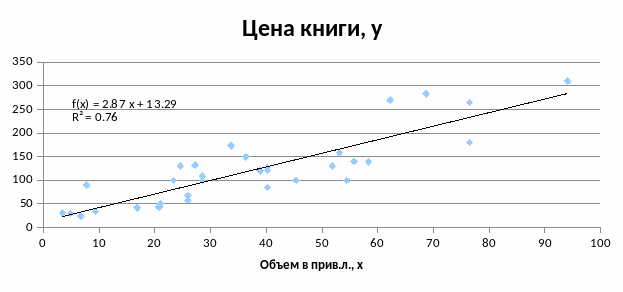
Степенная функция

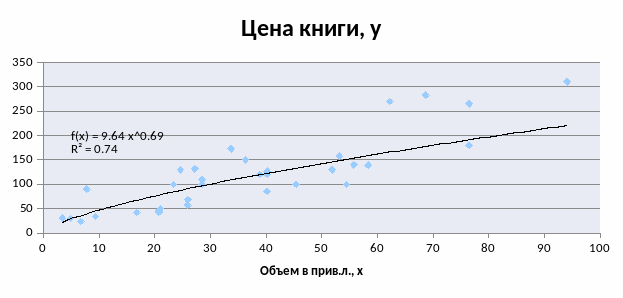
Экспоненциальная функция

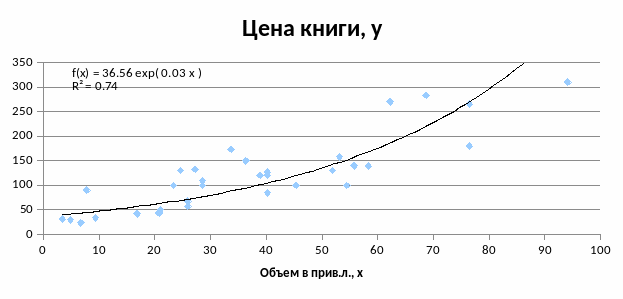
Логарифмическая функция

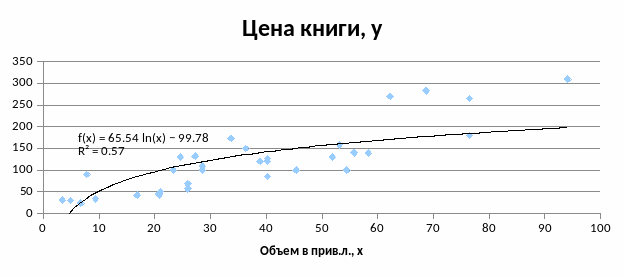
Обратная

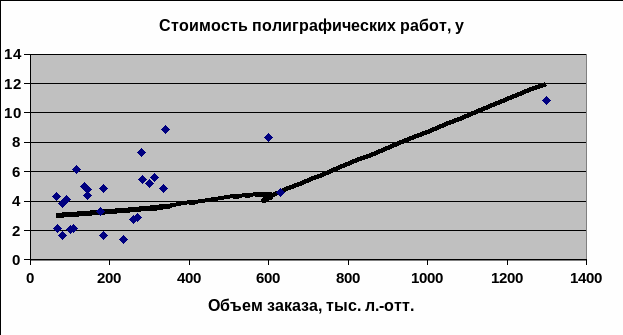
Гиперболическая

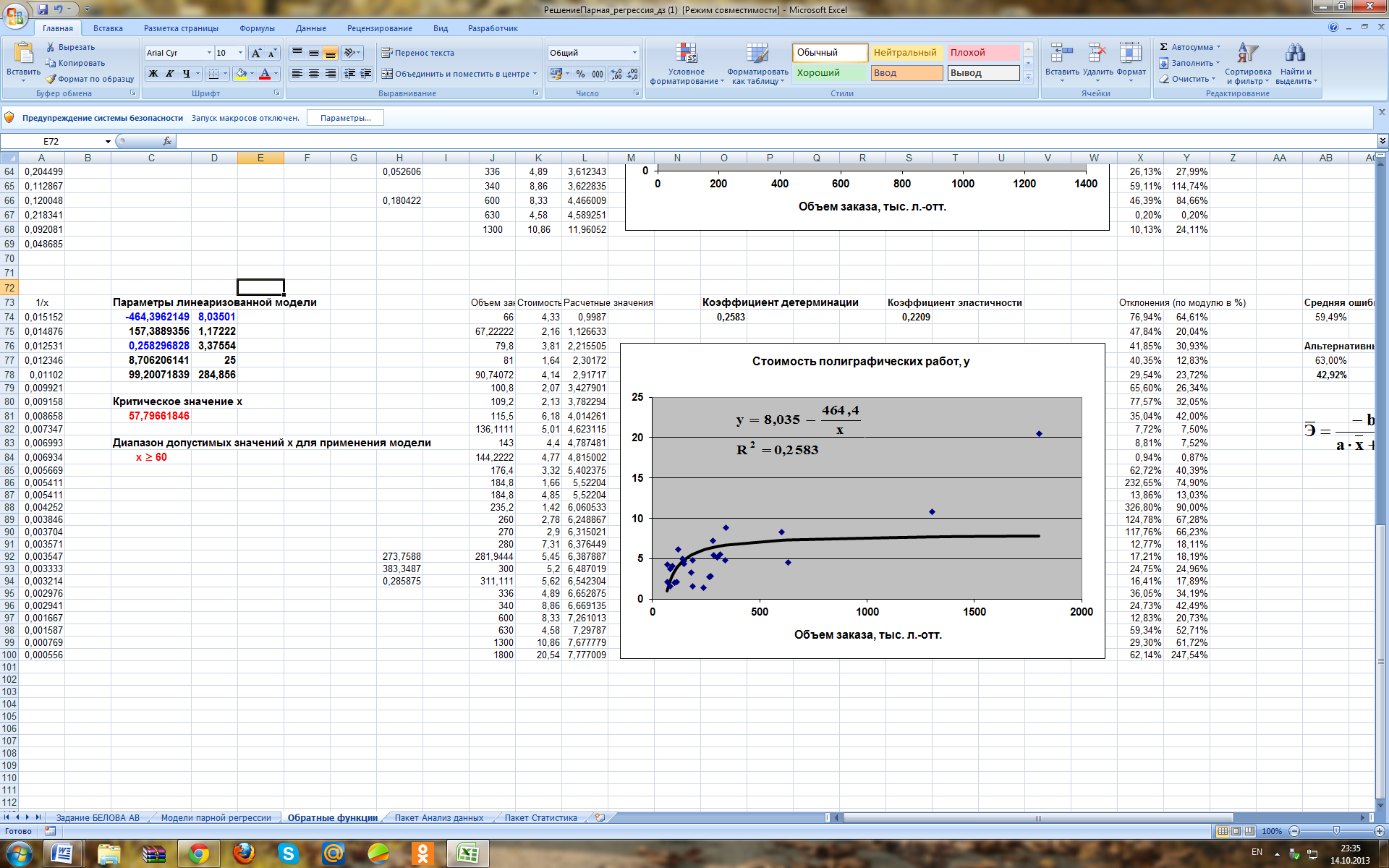
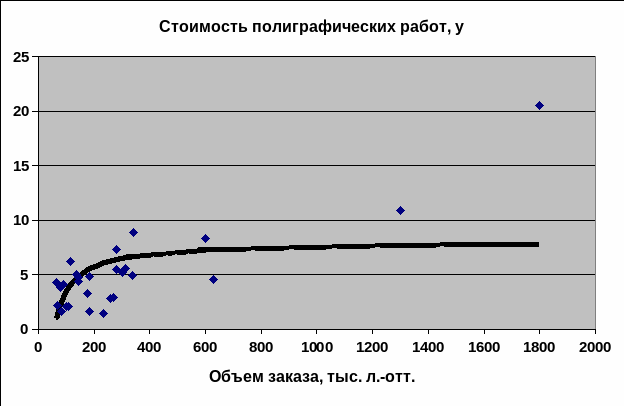
Расчетные формулы Коэффициент детерминации

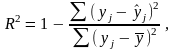
где 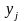- наблюдавшееся значение результативного показателя;

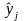- расчетное значение по уравнению регрессии;

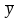- среднее значение результативного показателя.

Коэффициент детерминации рассчитывался для степенной функции регрессии:

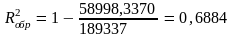
для экспоненциальной функции регрессии:

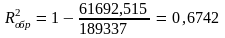
для обратной функции регрессии:

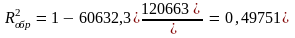
и для гиперболической функции регрессии:

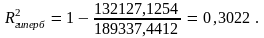
Коэффициент детерминации для линейной и логарифмической функций получен с помощью команды Excel: Диаграмма_Добавить линию тренда.

Средняя ошибка аппроксимации

Для расчета средней ошибки аппроксимации использовались формулы:

,

.

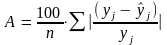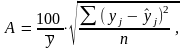
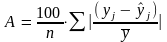Для каждой модели выбиралось минимальное из трех рассчитанных значений.

Коэффициент эластичности

Для линейной функции:

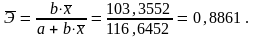
Для степенной функции:

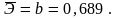
Для экспоненциальной функции:

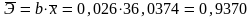
Для логарифмической функции:

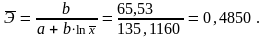
Для обратной функции:

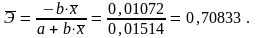
Для гиперболической функции:

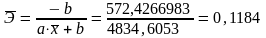
Сравнительная характеристика моделей

Вид модели	Коэффициент детерминации	Средняя ошибка аппроксимации	Коэффициент эластичности
Линейная	0,762	30,88%	0,8861
Степенная	0,6884	30,21%	0,689
Экспоненциальная	0,6742	30,36%	0,9370
Логарифмическая	0,5742	48,72%	0,4850
Обратная	0,49751	30,42%	0,70833
Гиперболическая	0,3022	61,07%	0,1184

Из рассмотренных моделей наибольшее значение коэффициента детерминации, близкое к требуемой величине 0.762, имеют линейная и экспоненциальная модели. Однако, высокая величина средней ошибки аппроксимации (около 61%) ограничивает возможность их практического применения. Ни одна из других моделей не соответствует предъявляемым требованиям по величине коэффициента детерминации и средней ошибки аппроксимации.

Расчетные формулы для определения параметров регрессии и корреляции

Система нормальных линейных алгебраических уравнений относительно параметров парной линейной регрессии

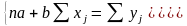
Решение системы: a = 13,293; b = 2,8688.

Коэффициент регрессии (альтернативные формулы)

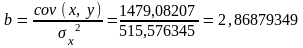
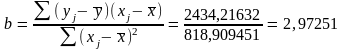
Свободный член уравнения регрессии

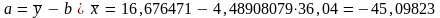
Коэффициент корреляции

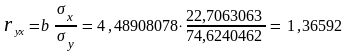
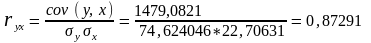
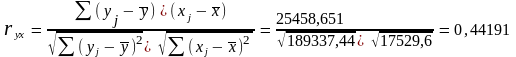
Индекс корреляции

.

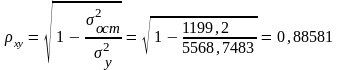
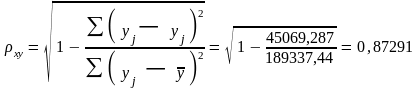Коэффициент детерминации

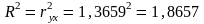(для парной линейной регрессии).

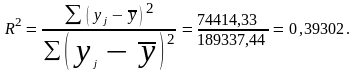
Скорректированный коэффициент детерминации

Более 75% дисперсии результативного показателя (Стоимость полиграфических работ) обусловлено изменением фактора-аргумента (Объем заказа в тыс. л.-отт.). По этому показателю рассматриваемая модель регрессии удовлетворяет необходимым требованиям.

Стандартная ошибка регрессии

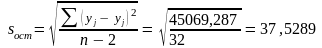
F-критерий Фишера

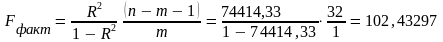
F_табл =FРАСПОБР(0.05;1;25) = 4,1491

F_табл =FРАСПОБР(0.01;1;11) = 7,49928

При уровне значимости  = 0,05 и при более строгом подходе ( = 0,01) уравнение регрессии в целом является значимым.

Стандартные ошибки параметров регрессии и коэффициента корреляции

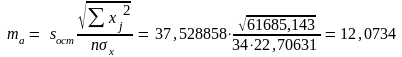
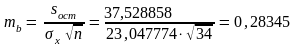
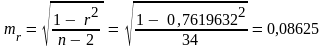
Расчетные значения T-критериев Стьюдента

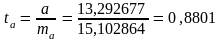
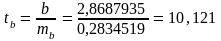
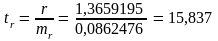
Соотношение между T-критериями Стьюдента и F-критерием Фишера

Табличное значение T-критерия Стьюдента

T_табл =СТЬЮДРАСПОБР(0.05;25) = 2,03693

T_табл =СТЬЮДРАСПОБР(0.01;25) = 2,73848

При уровне значимости  = 0,05 и при  = 0,01 параметры уравнения регрессии a и b, а также коэффициент корреляции r являются значимыми.

Точечный прогноз

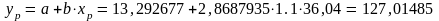
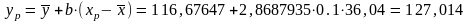
Ошибка прогноза

Доверительный интервал прогноза с учетом индивидуального рассеивания результирующего показателя при x = 1.1x_средн.

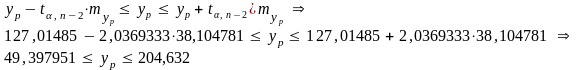
Доверительный интервал прогноза без учета индивидуального рассеивания результирующего показателя при x = 1.1x_средн.

	Стандартная ошибка			6,5167
	точечного прогноза y
	Нижняя доверительная			113,741
	граница прогноза
	Верхняя доверительная			140,289
	граница прогноза

Доверительные интервалы прогноза с учетом и без учета индивидуального рассеивания результирующего показателя при различных значениях x