Лабораторная работа №1

Исследование линейных систем регулирования

Цель работы: Исследуя линейные системы изучить временные и частотные характеристики типовых динамических звеньев.

Краткая теория.

Под типовым звеном понимают такое звено динамики, которое описывается уравнением не выше второго порядка. (n<2)

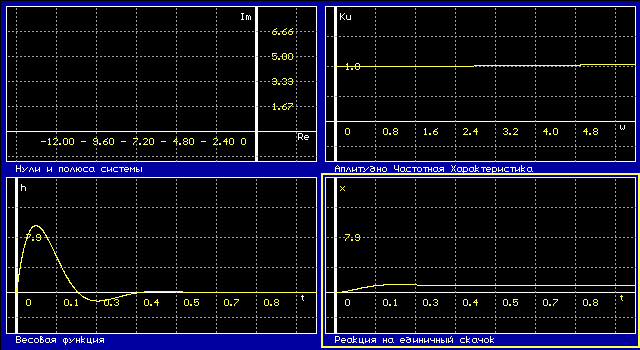
Динамические свойства звена могут быть определены по его переходной функции и функции веса.

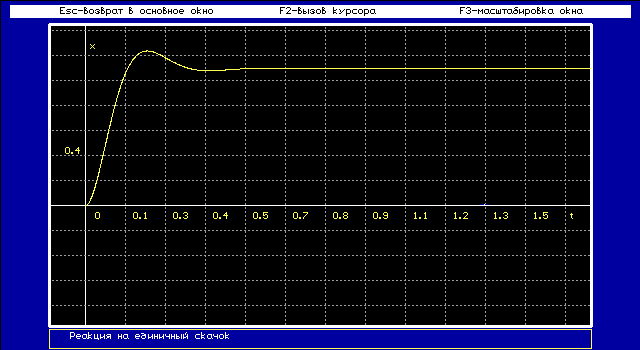
Переходная функция, или переходная характеристика, h(t) описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице. Такое входное воздействие называется единичной ступенчатой функцией

Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход.

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Для наглядного представления частотных свойств звена используются так называемые частотные характеристики.

Амплитудно-фазовая частотная характеристика (а.ф.х.) строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции W(jw) = U(w) + jV(w) при изменении частоты от нуля до бесконечности.

Вместо а.ф.х. можно построить отдельно амплитудно-частотную характеристику (а.ч.х.) и фазочастотную характеристику (ф.ч.х.).

Амплитудно-фазовая частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.

Фазочастотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах.

Ход работы:

2.1.Исследовать безынерционное звено: W (p) = K.

K=14.

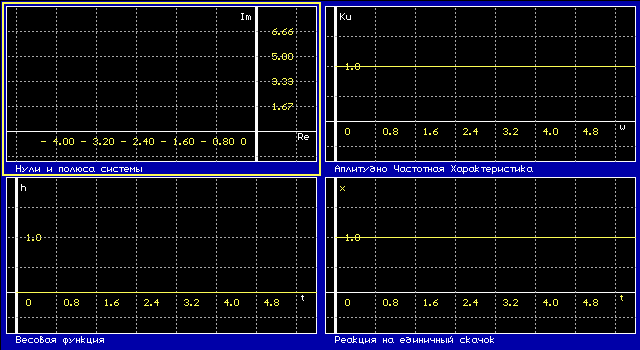
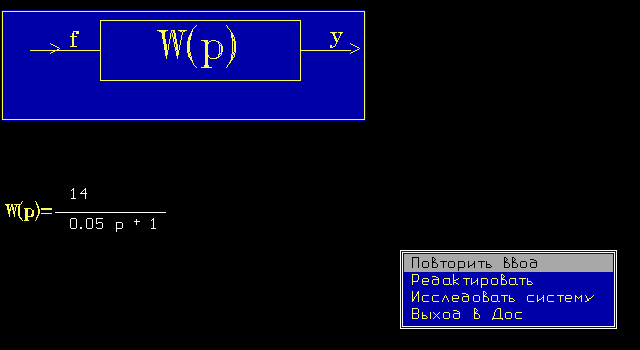
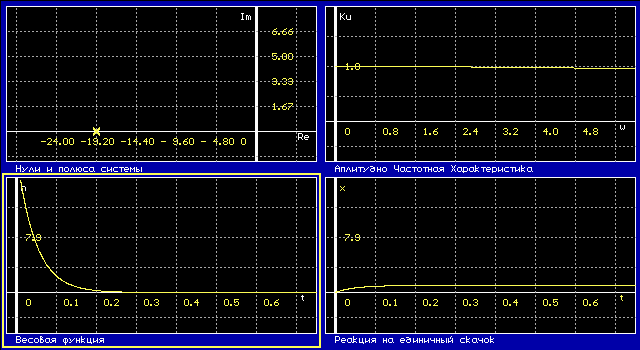
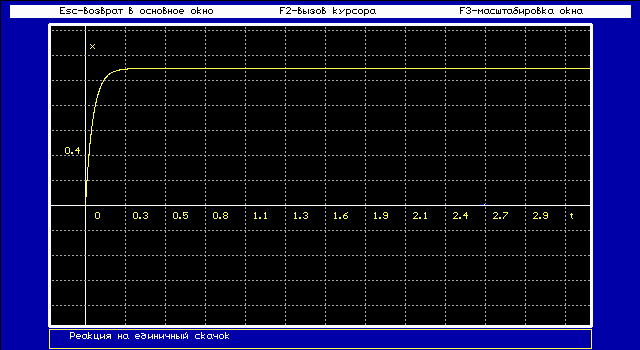
2.2. Исследовать апериодическое звено первого порядка: W (p) = K

Tp+1

К = 14

T = 0,05

2.3.Исследовать апериодическое звено второго порядка:

K=14

W (p) = K T1=0.06

T1T2 p² + T1p + 1 T2=0.05

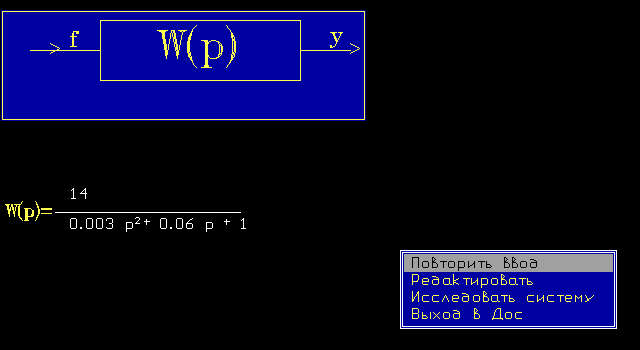
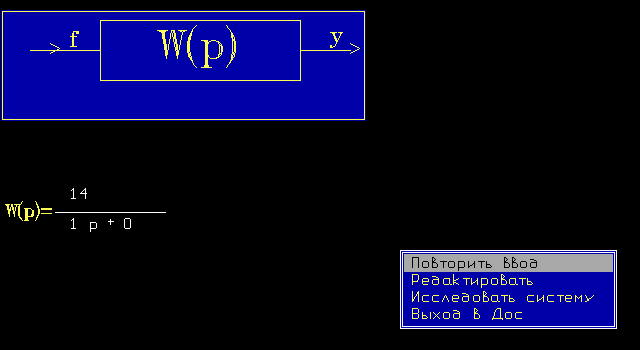
2.4. Исследовать идеальное интегрирующее звено: W (p) = K/p

K = 14

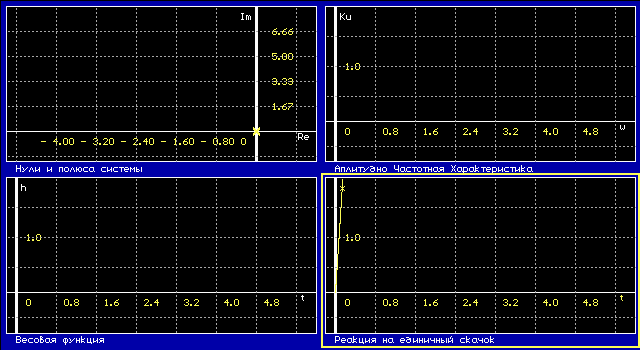
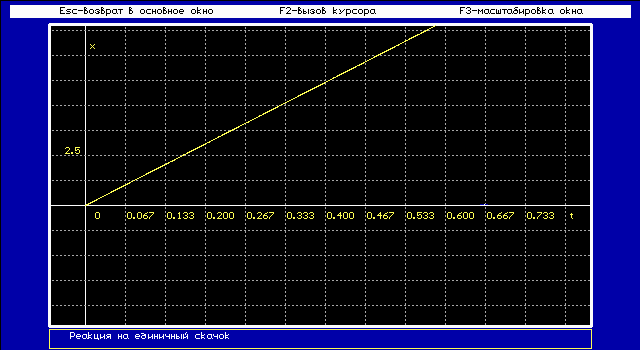
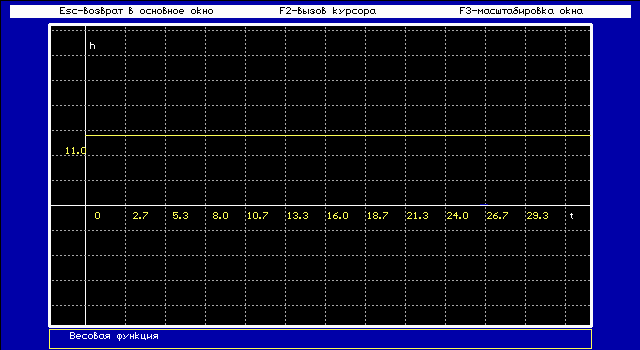
2.5. Исследовать реальное интегрирующее звено: K/p (Tp+1)

K = 14

T = 0,05

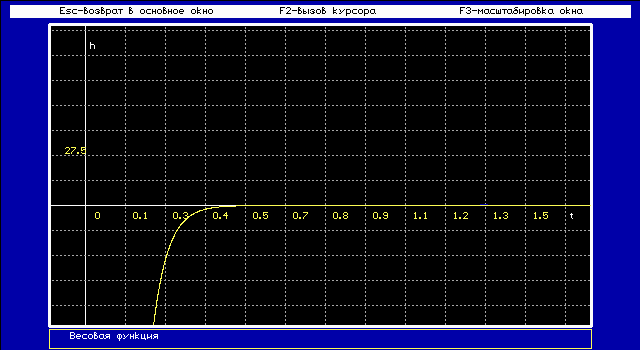
2.6. Исследовать реальное дифференцирующее звено: K/p (Tp+1)

K = 14

T = 0,05

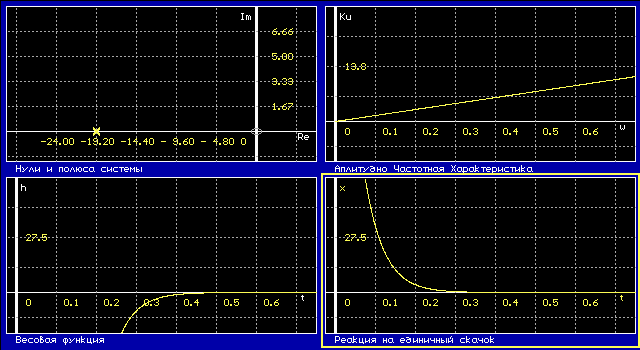
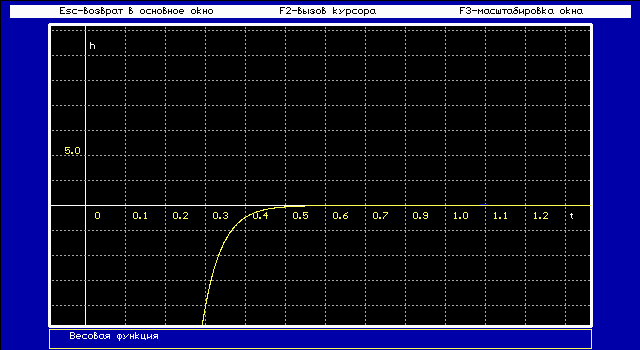
2.7. Вывод: Исследуя линейные системы, мы изучили временные и частотные характеристики типовых динамических звеньев. Динамические свойства звена могут быть определены по его временной характеристике, т.е. переходной функции и функции веса. Переходная функция описывает скачкообразное воздействие при величине скачка, равной единице, а функция веса описывает реакцию на это воздействие. Для наглядного представления частотных свойств звена мы использовали так называемые частотные характеристики. Амплитудно-фазовая частотная характеристика (а.ф.х.), она реагирует на изменение частоты сигнала. Вместо а.ф.х. можно построить отдельно амплитудно-частотную характеристику (а.ч.х.) и фазочастотную характеристику (ф.ч.х.). Амплитудно-фазовая частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.

Фазочастотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах. Что мы наглядно показали в лабораторной работе.