§ 3.4. Абсолютно упругий удар

Удар (соударение). Столкновение двух или более тел, при котором взаимодействие длится очень короткое время.

Центральный удар. Удар, при котором тела от удара движутся вдоль прямой, проходящей через их центры масс. Здесь рассматриваются только центральные удары.

Абсолютно упругий удар. Столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии.

Прямой центральный удар.

В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой, соединяющей их центры. Проекции векторов скорости на линию удара равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицательное – движению влево. При указанных допущениях законы сохранения имеют вид

– сохранение импульса

, (3.17)

– сохранение энергии

. (3.18)

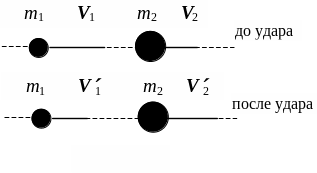
Рис. 3.4

Для определения скоростей шаров после удара, и , необходимо решить систему уравнений (3.17) и (3.18). Уравнение (3.18) является квадратным, поэтому система уравнений имеет два набора решений, одно из которых является тривиальным, и . Оно соответствует случаю, в котором столкновение шаров не происходит (их скорости не меняются), поэтому эту возможность мы не будет рассматривать в дальнейшем.

Второй набор решений соответствует случаю столкновения шаров, так как он реализуется при условии, что и . Для упрощения процедуры нахождения решений системы уравнений (3.17) и (3.18) заменим квадратное уравнение (3.18) линейным уравнением. Для этого перепишем систему уравнений в виде

,

.

Деля левую часть второго уравнения на левую часть первого и, проделывая ту же операцию с правыми частями уравнений, получим линейное уравнение

. (3.18а)

Решая систему линейных уравнений (3.17) и (3.18а) относительно и , находим скорости шаров после удара:

, (3.19)

, (3.20)

где – скорость центра масс шаров.

§ 3.5. Абсолютно неупругий удар

Абсолютно неупругий удар. Столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.

Согласно закону сохранения импульса,

(3.21)

(m₁ и m₂ – массы шаров, V₁ и V₂ – скорости шаров до удара, V – скорость шаров после удара). Тогда

. (3.22)

Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае если массы шаров равны (m₁ = m₂), то

. (3.23)

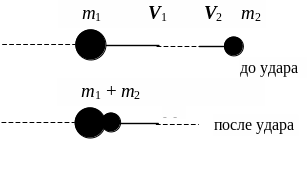
Рис. 3.5

Пример: шары из пластилина (или глины), движущиеся навстречу друг другу.

В данном случае закон сохранения механической энергии не соблюдается. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту «потерю» можно определить по разности кинетической энергии тел до и после удара:

,

или с учетом (3.22) получим

, (3.24)

где – приведенная масса.

Если ударяемое тело было первоначально неподвижно (V₂ = 0), то

(3.25)

Если m₂ >> m₁, то V << V₁ и почти вся кинетическая энергия при ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молотка.