§ 8.5. Закон Максвелла о распределении молекул по скоростям

Движение молекул газа подчиняется законам статистической фи­зики. В среднем скорости и энергии всех молекул одинаковы. Од­нако в каждый момент времени энергия и скорости отдельных молекул могут значительно отличаться от среднего значения.

С помощью теории вероятности Максвеллу удалось вывести формулу для относительной частоты, с которой в газе при данной температуре встречаются молекулы со скоростями в определенном интервале значений.

Закон распределения Максвелла определяет относительное число молекул dN/N, скорости которых лежат в интервале (,  + d). Оно имеет вид:

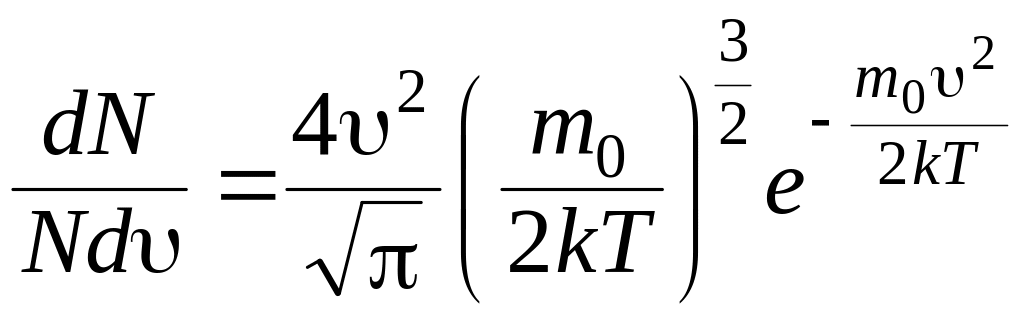(8.29)

где N – общее число молекул газа; – число молекул, скорости которых заключены в определенном интервале;  – нижняя граница интервала скоростей; d – величина интервала скоростей; T– температура газа; e = 2,718… – основание натуральных логарифмов;

k = 1,3810^-23 Дж/К – постоянная Больцмана; m₀ – масса молекулы.

При получении этой формулы Максвелл основывался на следующих предположениях:

1. Газ состоит из большого числа N одинаковых молекул.

2. Температура газа постоянна.

3. Молекулы газа совершают тепловое хаотическое движение.

4. На газ не действуют силовые поля.

Отметим, что под знаком экспоненты в формуле (8.29) стоит отношение кинетической энергии молекулы к величине kT, характеризующей среднее (по молекулам) значение этой энергии.

Распределение Максвелла показывает, какая доля dN/N общего числа молекул данного газа обладает скоростью в интервале от  до  + d.

График функций распределения (рис. 8.5) асимметричен. Положение максимума характеризует наиболее часто встречающуюся скорость, которую называют наиболее вероятной скоростью _m. Скорости, превышающие _m, встречаются чаще, чем меньшие скорости. С повышением температуры максимум распределения сдвигается в направлении больших скоростей.

Одновременно кривая становится более плоской (площадь, заключенная под кривой, не может измениться, так как число молекул N остается постоянным).

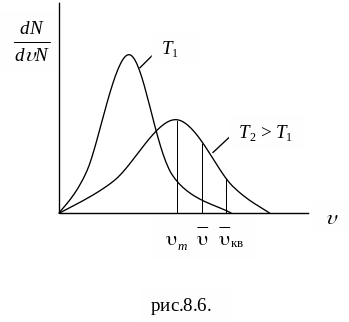
Рис. 8.5

Для определения наиболее вероятной скорости нужно исследовать на максимум функцию распределения Максвелла (приравнять первую производную к нулю и решить относительно ). В результате получаем

.

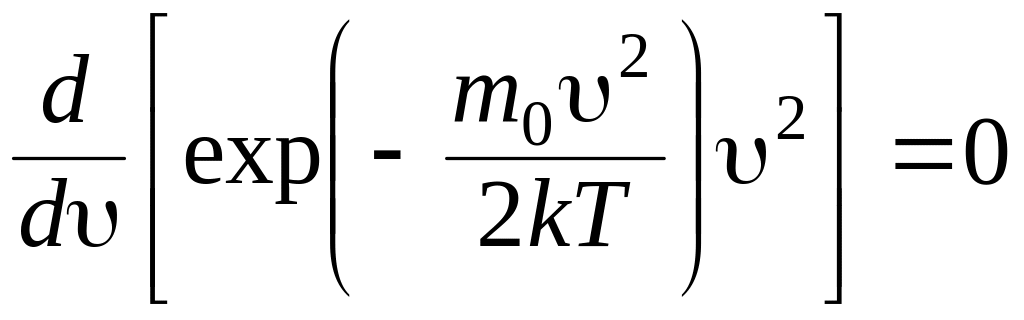Мы опустили множители, не зависящие от . Осуществив дифференцирование, придем к уравнению

.

Первый сомножитель (экспонента) обращается в нуль при  = , а третий сомножитель () при  = 0. Однако из графика (рис. 8.5) видно, что значения  = 0 и  =  соответствуют минимумам функции (8.29). Следовательно, значение , отвечающее максимуму, получается из равенства нулю второй скобки: . Отсюда

. (8.30)

Введем обозначения для функции распределения молекул по скоростям (8.29):

. (8.31)

Известно, что среднее значение некоторой физической величины (x) можно вычислить по формуле

. (8.32)

Из (8.32) получим выражения для среднего значения модуля скорости  и среднего значения квадрата :

, (8.33)

. (8.34)

Таким образом, средняя скорость молекул (ее называют также средней арифметической скоростью) имеет значение

. (8.35)

Квадратный корень из выражения (8.34) дает среднюю квадратичную скорость молекул:

. (8.36)

Отметим, что она совпадает с формулой (8.24). На рис. 8.5 приведен график функции распределения Максвелла. Вертикальными линиями отмечены три характерные скорости .