§ 8.4. Средняя энергия молекул

Из равенств (8.20), (8.21) и (8.22) следует, что

. (8.23)

Таким образом, термодинамическая температура есть величина пропорциональная средней энергии поступательного движения молекул.

Следует подчеркнуть, что средняя энергия молекул зависит только от температуры и не зависит от массы молекулы.

Получим выражение для средней квадратичной скорости молекул. Последняя определяется как

. (8.24)

Из формулы (8.18) следует, что средняя квадратичная скорость молекул есть

, (8.25)

где m – масса молекулы.

Только поступательно движутся лишь одноатомные молекулы. Двух- и многоатомные молекулы, кроме поступательного, могут совершать также вращательное и колебательное движения. Число независимых видов движения абсолютно твердого тела определяется числом степеней свободы.

Число независимых переменных, полностью определяющих положение системы в пространстве, называется числом степеней свободы.

Положение материальной точки определяется значениями трех ее координат, например, декартовых координат x, y, z. В соответствии с этим материальная точка имеет три степени свободы.

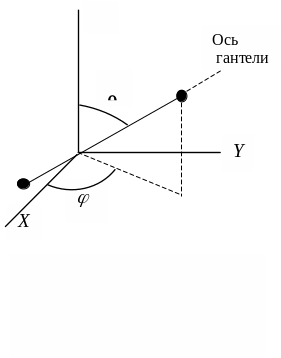
Рис. 8.3 Ориентация двухатомной молекулы (гантели) определяется заданием углов  и 

Если двухатомную молекулу представить в виде двух материальных точек, находящихся на расстоянии l друг от друга (форма гантели), которое остается неизменным, то число степеней свободы равно пяти. Действительно положение в пространстве можно задать координатами x, y, z центра масс системы, а углы  и φ, определяют направление в пространстве прямой l (рис. 8.3). Следовательно, три степени свободы будут поступательными и две вращательными (вращение материальных точек вокруг оси гантели лишено смысла).

Экспериментально установлено, что при определении числа степеней свободы молекулы, атомы нужно рассматривать как материальные точки. Общая формула для числа степеней свободы многоатомной молекулы с жесткой связью имеет вид:

, (8.26)

где n – число атомов в молекуле; f – число жестких связей (перемычек) между атомами.

Для одноатомной молекулы газа	n = 1, f = 0, i = 3.
Для двухатомной молекулы газа (рис. 8.3)	n = 2, f = 1, i = 5.
Для трехатомной молекулы (рис. 8.4)	n = 3, f = 3, i = 6.

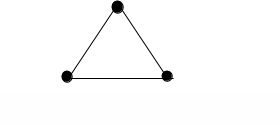
Рис. 8.4. Трехатомная молекула

Отметим, что для всех рассмотренных типов молекул число поступательных степеней свободы равно 3. Оставшиеся – приходятся на вращательные степени свободы. Кроме того, если в двухатомной молекуле две материальные точки связаны так, что между ними существует не жесткая связь, а действует упругая сила, то число степеней свободы увеличится на единицу и равно i = 6. Изменение расстояния l между точками обуславливается колебаниями в системе, в связи с чем степень свободы, соответствующую изменениям l, называют колебательной.

Согласно закону равнораспределения энергии по степеням свободы молекулы на каждую степень свободы (поступательную, вращательную и колебательную) в среднем приходится одинаковая кинетическая энергия, равная kT/2.

Система, совершающая гармонические колебания, называется гармоническим осциллятором. В теории колебаний доказывается что средние значения кинетической и потенциальной энергий гармонического осциллятора одинаковы. Отсюда следует, что колебательная степень свободы молекулы обладает удвоенной энергетической емкостью, т. е. равна kT.

Итак, из закона равнораспределения энергии по степеням свободы следует:

, (8.27)

где

. (8.28)