Контрольные вопросы

1. Возможно ли образование сходящейся сферической волны?

2. Что понимается под уравнением волны и волновым уравнением?

3. Каковы должны быть свойства среды, чтобы для механических волн в этой среде выполнялся принцип суперпозиции?

4. Каков физический смысл групповой скорости?

5. От чего зависит фазовая скорость волн в упругой среде?

Задачи

1. При отражении от преграды в образующихся стоячих волнах отношение амплитуды в пучности к амплитуде в узле равно . Какая часть энергии уходит за преграду?

2. Волна распространяется в среде с затуханием. На графике по оси абсцисс отложено расстояние от источника колебаний, причем это расстояние выражено в длинах волн. По оси ординат отложен десятичный логарифм амплитуды. Написать на основании этого графика формулу, представляющую зависимость амплитуды от расстояния.

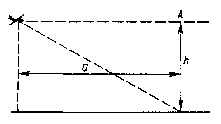
3. Самолет летит над землёй на высоте h со сверхзвуковой скоростью. На каком наименьшем расстоянии a (по горизонтали) от стоящего на земле наблюдателя должна находится такая точка, из которой звук самолёта доходит до наблюдателя раньше, чем из точки A над его головой?

4. Складываются два одинаково направленных колебания: , . Сравнить амплитуду А с амплитудой результирующего колебания.

Глава 8 Основы молекулярной физики и термодинамики § 8.1. Статистический и термодинамический методы исследования

Макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул изучает молекулярная физика и термодинамика.

Молекулярная физика это раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Термодинамика это раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.

Существует два способа описания процессов, происходящих в макроскопических телах (т. е. телах, состоящих из очень большого числа частиц-атомов и молекул), – статистический и термодинамический.

Статистической физикой называется раздел физики, посвященный изучению свойств макроскопических тел, исходя из свойств образующих тело частиц и взаимодействий между ними.

Статистический метод составляет основу молекулярной физики, это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними значениями физических величин, характеризующих всю совокупность частиц (например, средние значения скоростей теплового движения молекул и их энергий).

В отличие от статистического метода, термодинамический метод, нацелен на исследование систем из большого числа частиц, не рассматривая ее микроструктуры и совершающихся в системе микропроцессов. Данный метод оперирует величинами, характеризующими систему в целом (например, давление, объем, температура), на основе законов сохранения энергии.

Термодинамической системой называется совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Примером может служить жидкость и находящийся в соприкосновении с ней пар или газ.

Термодинамические системы не обменивающиеся с внешней средой ни энергией, ни веществом, называются изолированными или замкнутыми.

Термодинамическими параметрами или параметрами состояния называется совокупность физических величин, характеризующих свойства термодинамической системы. Обычно это температура (T), давление (p) и объем (V).

Состояние, в котором хотя бы один из параметров не имеет определенного значения, называется неравновесным.

Состояние термодинамической системы называется равновесным, если все термодинамические параметры имеют определенные значения, не изменяющиеся с течением времени.

Термодинамическим процессом называется переход системы из одного состояния в другое, при котором происходит изменение хотя бы одного из ее термодинамических параметров. Говорят, что система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется, а соответствующий процесс называется равновесным или квазистатическим (почти статическим).

Если по координатным осям откладывать значения каких-либо двух параметров (p и V, p и T, и т. д.), то равновесное состояние системы можно изобразить точкой на координатной плоскости (рис. 8.1), а термодинамический процесс – сплошной линией. Стрелка на линии указывает направление процесса.

Процесс, при котором система после ряда изменений возвращается в исходное состояние, называется круговым процессом или циклом. Обратимый цикл изображается на координатной плоскости замкнутой кривой (1–2–1).

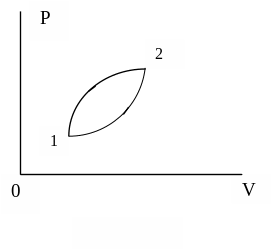
Рис. 8.1