§ 7.2. Уравнение плоской и сферической волн

Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t:

Ψ = Ψ(x, y, z; t) (7.3)

(имеются ввиду координаты равновесного положения частицы).

Найдем вид функции Ψ в случае плоской волны, предполагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, чтобы ось X совпала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси x и, поскольку все точки волновой поверхности колеблются одинаково, смещение Ψ будет зависеть только от x и t: Ψ = Ψ(x, t).

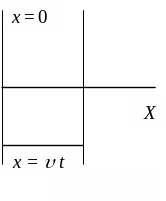
Рис. 7.3

Пусть колебания точек, лежащих в плоскости x = 0 (рис.7.3), имеют вид

Ψ(0, t) = acos(t + ).

Найдем вид колебания точек в плоскости, соответствующей произвольному значению x. Для того чтобы пройти путь от плоскости x = 0 до этой плоскости, волне требуется время  = x/ ( скорость распространения волны). Следовательно, колебания частиц, лежащих в плоскости x, будут отставать по времени на  от колебаний частиц в плоскости x = 0, т. е. будут иметь вид

.

Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси x, выглядит следующим образом:

Ψ . (7.4)

Зафиксируем какое либо значение фазы, стоящей в уравнении (7.4), положив

. (7.5)

Это выражение определяет связь между временем t и тем местом x, в котором фаза имеет зафиксированное значение. Вытекающее из него значение dx/dt дает скорость, с которой перемещается данное значение фазы. Продифференцировав выражение (7.5), получим

,

откуда

. (7.6)

Таким образом, скорость распространения волны  в уравнении (7.4) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

Согласно (7.6) dx/dt  0. Следовательно, уравнение (7.4) описывает волну, распространяющуюся в сторону возрастания x. Волна, распространяющаяся в противоположном направлении, описывается уравнением

Ψ . (7.7)

Уравнению плоской волны можно придать симметричный относительно x и t вид. Для этого введем величину

, (7.8)

которая называется волновым числом. Умножив числитель и знаменатель выражения (7.8) на частоту v, можно представить волновое число в виде

. (7.9)

Раскрыв в (7.4) круглые скобки и приняв во внимание (7.9), придем к следующему уравнению плоской волны, распространяющемуся вдоль оси x:

. (7.10)

Уравнение волны, распространяющейся в сторону убывания x, отличается от (7.10) только знаком при члене kx:

. (7.11)

Теперь найдем уравнение сферической волны. Всякий реальный источник волн обладает некоторой протяженностью. Однако, если ограничится рассмотрением волны на расстояниях от источника, значительно превышающих его размеры, то источник можно считать точечным. В изотропной и однородной среде волна, порождаемая точечным источником, будет сферической. Допустим, что фаза колебаний источника равна . Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой (чтобы пройти путь r, волне требуется время  = r/). Амплитуда колебаний в этом случае убывает с расстоянием от источника по закону 1/r.

Следовательно, уравнение сферической волны имеет вид

, (7.12)

где   постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице.

Рассмотрим более общий случай плоской волны, распространяющийся в произвольном направлении. Для этого введем единичный вектор n нормали к волновой поверхности.

Вектор

k = k n, (7.13)

равный по модулю волновому числу и имеющий направление нормали к волновой поверхности, называется волновым вектором. Общее уравнение плоской волны можно представить в виде

Ψ . (7.14)

Мы получили уравнение плоской незатухающей волны, распространяющейся в направлении, определяемом волновым вектором k.