§ 6.7. Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления F^* пропорциональна скорости:

. (6.36)

Здесь r – постоянная, называемая коэффициентом сопротивления.

Знак минус обусловлен тем, что сила F^* и скорость V имеют противоположные направления; следовательно, их проекции на ось X имеют разные знаки.

Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид

. (6.37)

Используя обозначения

, (6.38)

перепишем уравнение (6.37) следующим образом:

. (6.39)

Это дифференциальное уравнение описывает затухающие колебания системы.

Отметим, что представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при r = 0). Эту частоту называют собственной частотой системы.

При не слишком сильном затухании (  ₀) общее решение уравнения (6.39) имеет вид

x = a₀exp(–t)cos(t +). (6.40)

Здесь а₀ и  – произвольные постоянные;  – величина, определяемая формулой

. (6.41)

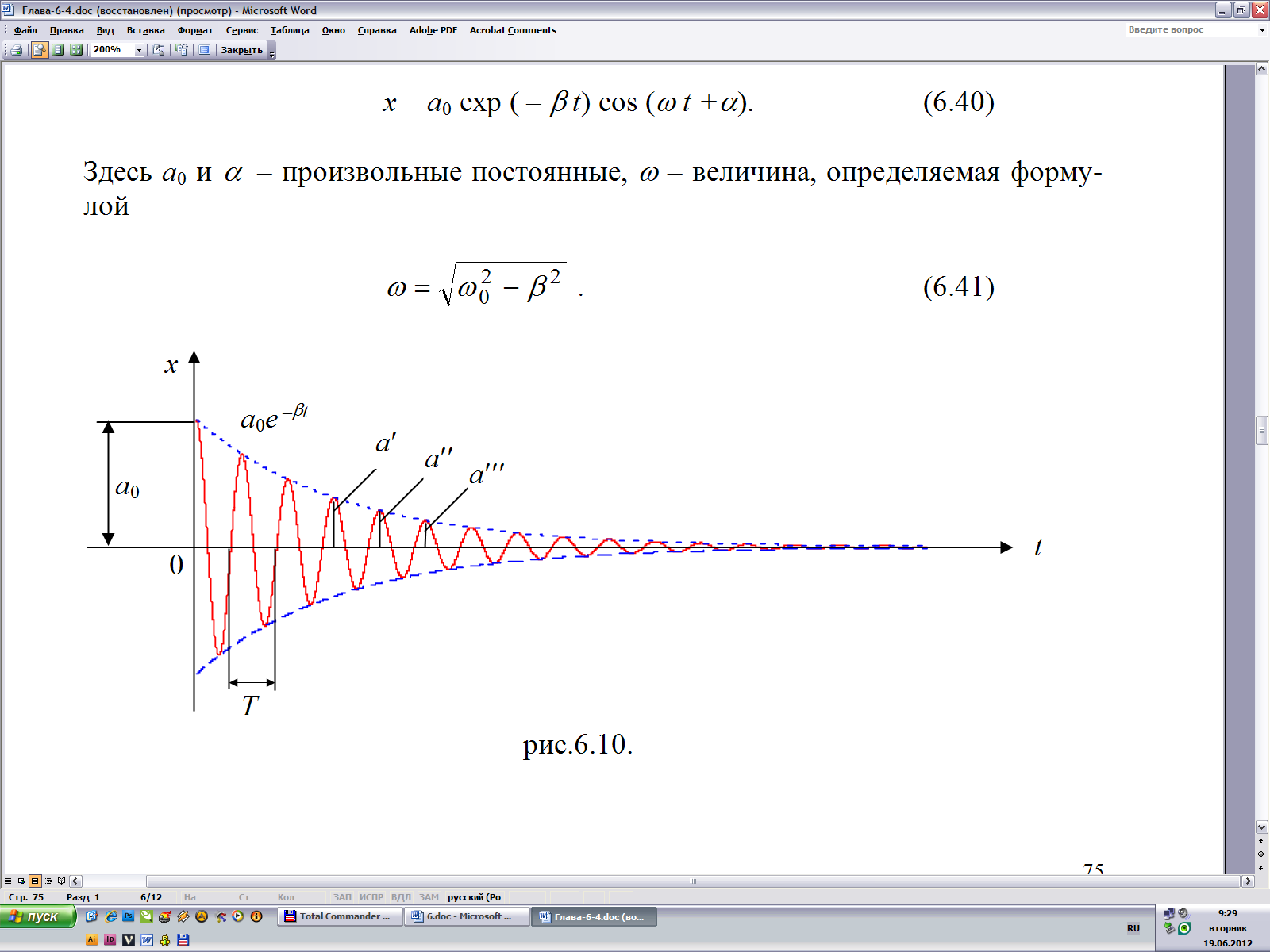
Рис. 6.10

На рис. 6.10 дан график функции (6.40). Штриховыми линиями показаны пределы, в которых находится смещение колеблющейся точки х. Движение системы можно рассматривать как гармоническое колебание с частотой  с амплитудой, изменяющейся по закону a(t) = a₀exp(–t).

Скорость затухания колебаний определяется величиной  = r/2m, которую называют коэффициентом затухания. Найдем время , за которое амплитуда уменьшается в е раз. По определению

exp(–) = exp(–1),

откуда  = 1. Следовательно, коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в е раз.

Вообще отношение значений амплитуд, соответствующих моментам времени, различающимся на период, равно

.

Это отношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания:

. (6.42)

Выразив в соответствии с (6.42)  через  и Т, можно закон убывания амплитуд со временем записать в виде

.

За время , за которое амплитуда уменьшается в е раз, система успевает совершить N_e = /T колебаний. Из условия exp[–(/T)] = exp(–1) получается, что (/Т) = N_e = 1. Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за тоже время, за которое амплитуда уменьшается в е раз.

Из формулы (6.41) следует, что с ростом коэффициента затухания период колебаний

(6.43)

увеличивается. При  = ₀ период колебаний обращается в бесконечность, т. е. движение перестает быть периодическим. При  > ₀ движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний. На рис. 6.11 показаны два возможных способа возвращения системы к положению равновесия при апериодическом движении. Каким из этих способов система приходит в положение равновесия, зависит от начальных условий. Движение, изображаемое кривой 2, получается в том случае, когда система начинает двигаться из положения, характеризуемого смещением х₀, к положению равновесия с начальной скоростью V₀. Это условие будет выполнено в том случае, если выведенной из положения равновесия системе сообщить достаточно сильный толчок к положению равновесия. Если, отведя систему из положения равновесия, отпустить ее без толчка (т. е. с V₀ = 0), движение будет происходить в соответствии с кривой 1.

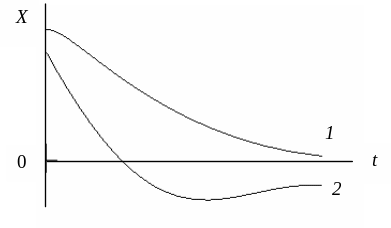
Рис. 6.11