§ 5.5. Основной закон релятивистской динамики
Релятивистский импульс определяется как
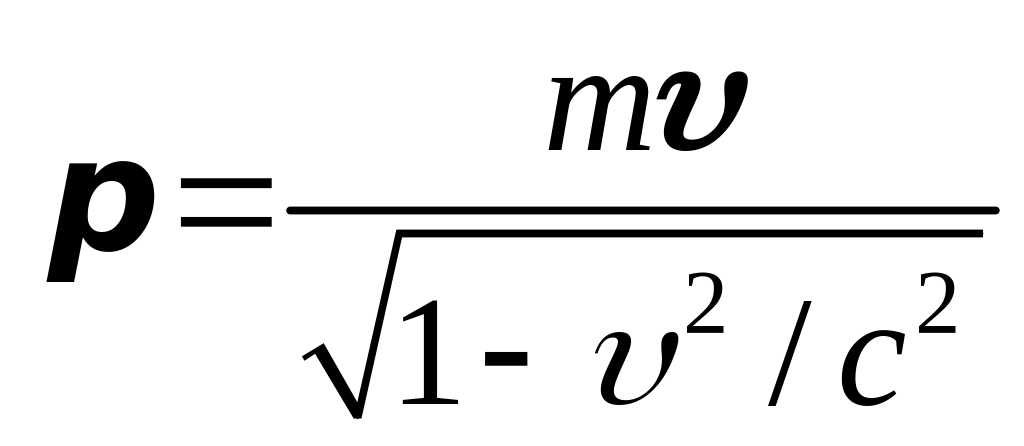, (5.22)
где m – масса частицы.
Закон сохранения релятивистскoго импульса гласит, что релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Из принципа относительности Эйнштейна (см. § 5.2), утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца.
Основной закон релятивистской динамики имеет вид:
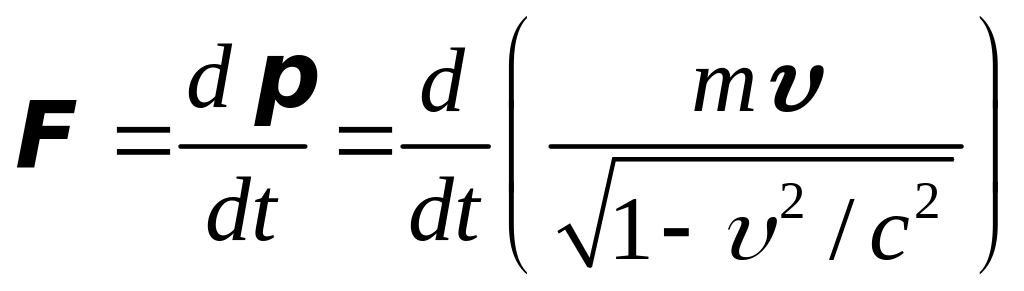, (5.23)
где
– релятивистский импульс материальной
точки.
Это уравнение инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами.
Из
приведенных формул (5.22) и (5.23) следует,
что при скоростях, значительно меньших
c,
они переходят в формулы классической
механики. Следовательно, условием
применимости законов классической
(ньютоновской) механики является условие
c.
Законы классической механики получаются
как следствие теории относительности
для предельного случая
c
(формально
переход осуществляется при
).
Таким образом, классическая
механика – это механика макротел,
движущихся с малыми скоростями (
по сравнению со скоростью света в
вакууме).
§ 5.6. Энергия в релятивистской динамике
Полная энергия релятивистской частицы определяется как
, (5.24)
где
– масса частицы,
– ее скорость. Полная энергия в разных
системах отсчета различна.
Энергия покоящегося тела (при
)
.
(5.25)
Классическая механика энергию покоя
не учитывает, считая, что при
энергия покоящегося тела равна нулю.
Закон сохранения энергии в релятивистской механике гласит, что полная энергия замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Кинетическая энергия тела определяется формулой
, (5.26)
поскольку полная энергия в релятивистской динамике — это сумма кинетической энергии и энергии покоя.
Из формул (5.22) и (5.24) легко получить выражение, связывающее энергию и импульс:
. (5.27)
Отсюда получим
. (5.28)
Учитывая, что
,
отсюда получим
. (5.29)
Контрольные вопросы
1. Какие принципы лежат в основе специальной теории относительности?
2. Как связаны друг с другом преобразования Галилея и преобразования Лоренца?
3. Какие вы знаете инвариантные величины?
4. Напишите формулу, выражающую импульс частицы через ее энергию и скорость.
5. Напишите формулу, выражающую энергию частицы через ее импульс.
6. Что характерно для частиц с нулевой массой?
7. Соблюдается ли закон сохранения импульса в специальной теории относительности?
Задачи
1. Во сколько раз замедляется ход времени при скорости движения часов = 240 000 км/с?
2. Найти относительную скорость двух частиц, движущихся навстречу друг другу со скоростью = c/2.
3. Написать выражение для полной энергии частицы, ее кинетической энергии, энергии покоя, импульса частицы. Каким соотношением связаны энергии и импульс релятивистской частицы?
4. В ходе эксперимента были определены импульс и энергия частицы. Найти ее скорость и массу.
5. Электрон начинает ускоряться в однородном электрическом поле, напряженность которого направлена вдоль оси x. Нарисовать качественно графики зависимости от x: а) полной E и кинетической К энергий электрона; б) импульса электрона; в) скорости электрона.
6. Почему при =c преобразования Лоренца теряют смысл?
7. Может ли при аннигиляции электрона (q= - e) и позитрона (q=+e) образоваться один фотон? Ответ обосновать с помощью законов сохранения энергии и импульса.