Глава 5 Элементы специальной теории относительности § 5.1. Механический принцип относительности. Преобразования Галилея

Механический принцип относительности утверждает, что законы динамики одинаковы во всех инерциальных системах отсчета.

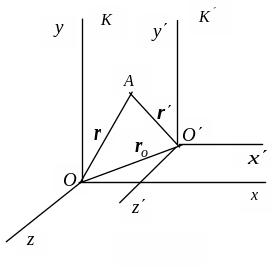
Рис. 5.1

Система движется относительно инерциальной системы К равномерно и прямолинейно со скоростью ( ). Скорость направлена вдоль O . Тогда = t.

Преобразования координат Галилея задают связь между радиусами-векторами или координатами произвольной точки A в обеих системах:

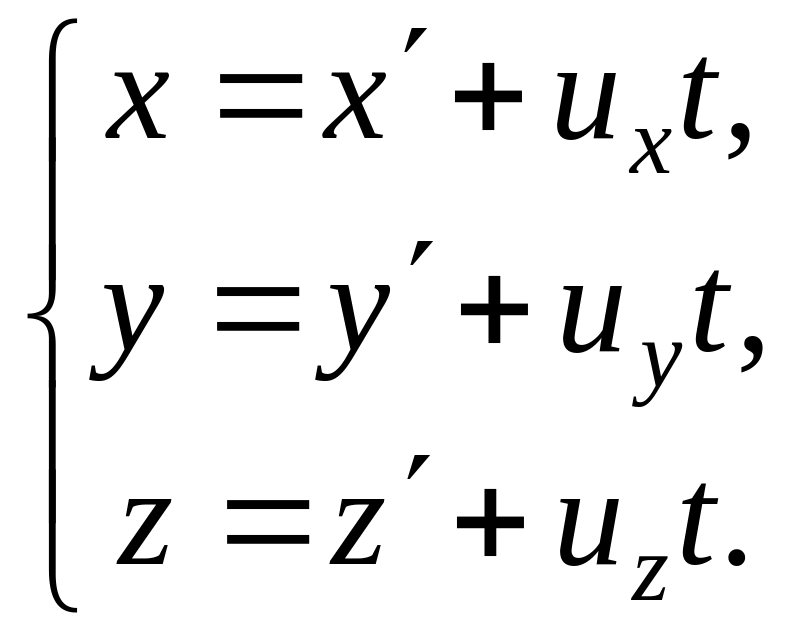= или (5.1)

Правило сложения скоростей в классической механике

Продифференцировав равенство по времени и учитывая, что в классической механике , получаем

(5.2)

Продифференцировав (5.2) по времени, получим соотношение для ускорений:

.

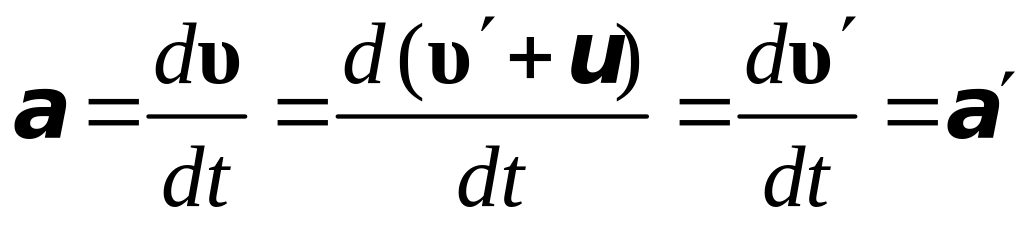Таким образом, имеем

(5.3)

т.е. система инерциальна (точка A движется относительно ее равномерно). Это и есть доказательство механического принципа относительности.

Записанные соотношения (5.1)–(5.3) справедливы лишь в классической механике ( c), где с – скорость света в вакууме м/с.

§ 5.2. Постулаты специальной теории относительности (сто). Преобразования Лоренца Постулаты Эйнштейна

I. Принцип относительности: никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможность обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны (неизменны) по отношению к переходу от одной инерциальной системы отсчета к другой.

II. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

Первый постулат Эйнштейна, являясь обобщением механического принципа относительности Галилея на любые физические процессы, утверждает, таким образом, что физические законы инвариантны по отношению к выбору инерциальной системы отсчета. Согласно этому постулату, все инерциальные системы отсчета совершенно равноправны. Согласно второму постулату Эйнштейна, постоянство скорости света – фундаментальное свойство природы, которое констатируется как опытный факт.

Преобразования Лоренца (при )

Система движется относительно системы K со скоростью вдоль оси X (рис. 5.2).

Преобразования Лоренца имеют следующий вид:

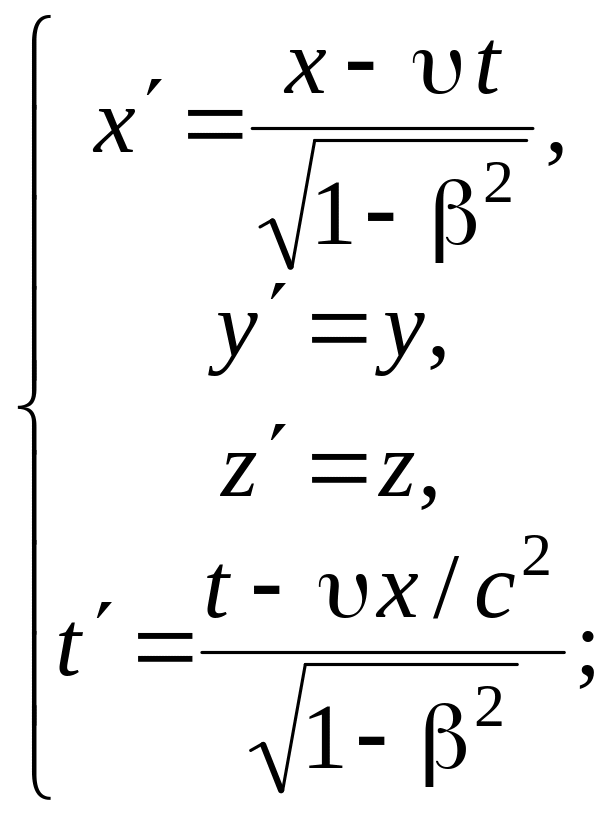
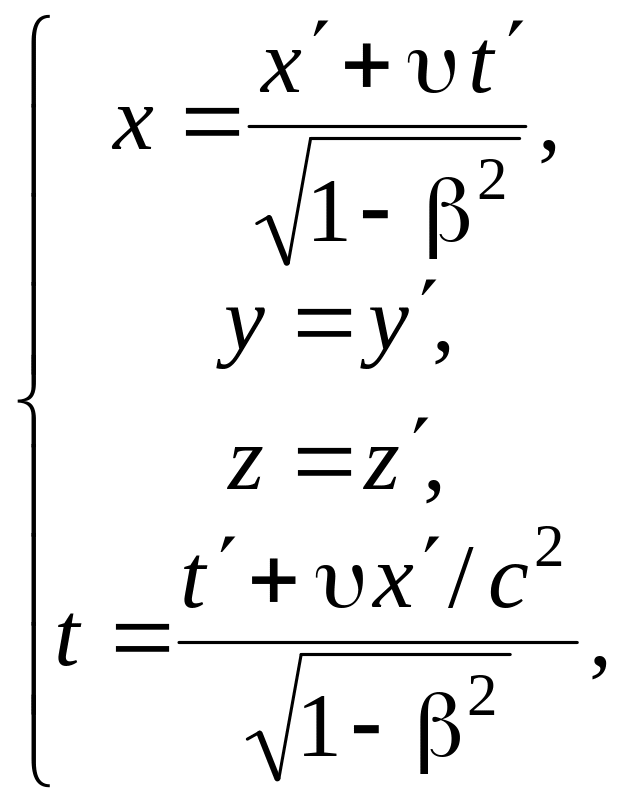(5.4)

где .

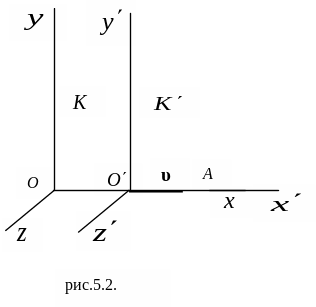
Рис. 5.2

1. Эти уравнения симметричны и отличаются лишь знаком при .

2. При  они переходят в классические преобразования Галилея (5.1).

3. В закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты (устанавливается взаимосвязь пространства и времени).

§ 5.3. Следствия из преобразований Лоренца Относительность одновременности

Пусть в системе в точках с координатами и в моменты времени и происходят два события. В системе им соответствуют координаты и и моменты и . Если события в системе происходят в одной точке ( ) и являются одновременными ( ), то, согласно преобразованиям Лоренца (5.4)

, , (5.5)

т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе пространственно разобщены ( ), но одновременны ( ), то в системе , согласно преобразованиям Лоренца (5.4)

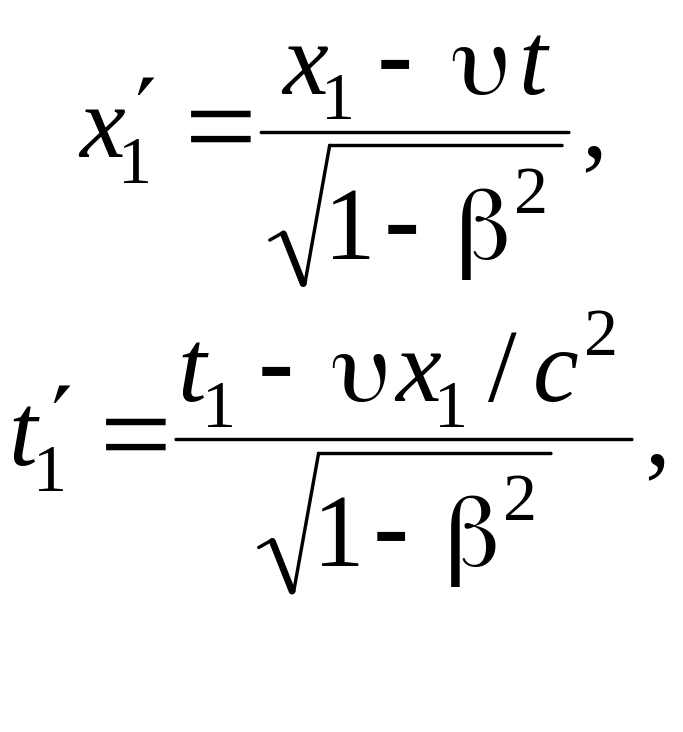
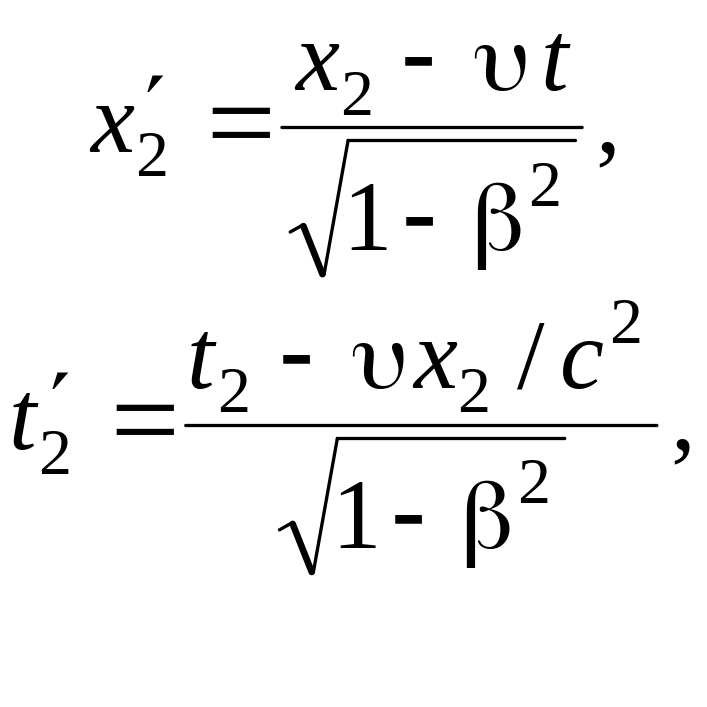(5.6)

Из (5.6) следует, что и . Таким образом, в системе эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.