Алгоритмические методы сглаживания временного ряда

Сглаживание с помощью пакета "Анализ данных" (простая скользящая средняя). Окно сглаживания равно 5

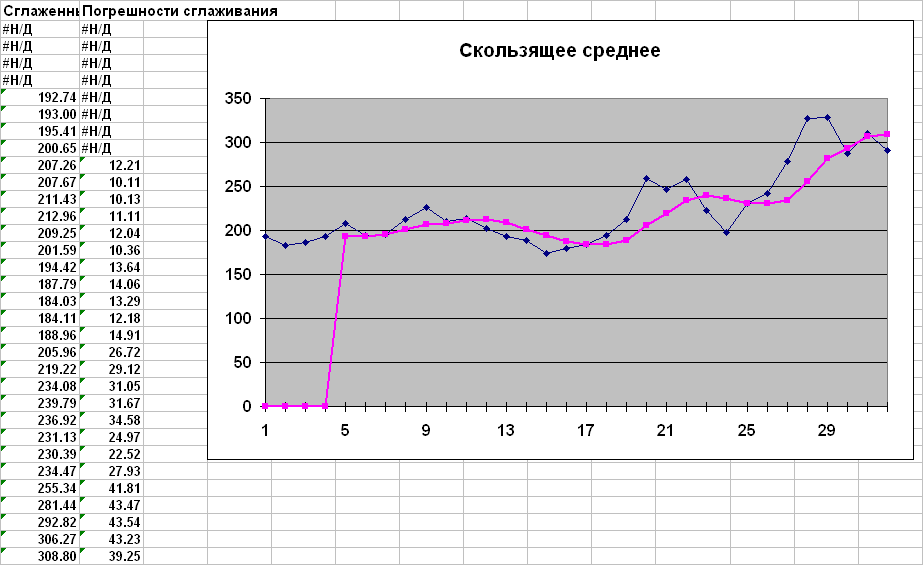
Сглаживание с помощью пакета STATISTICA

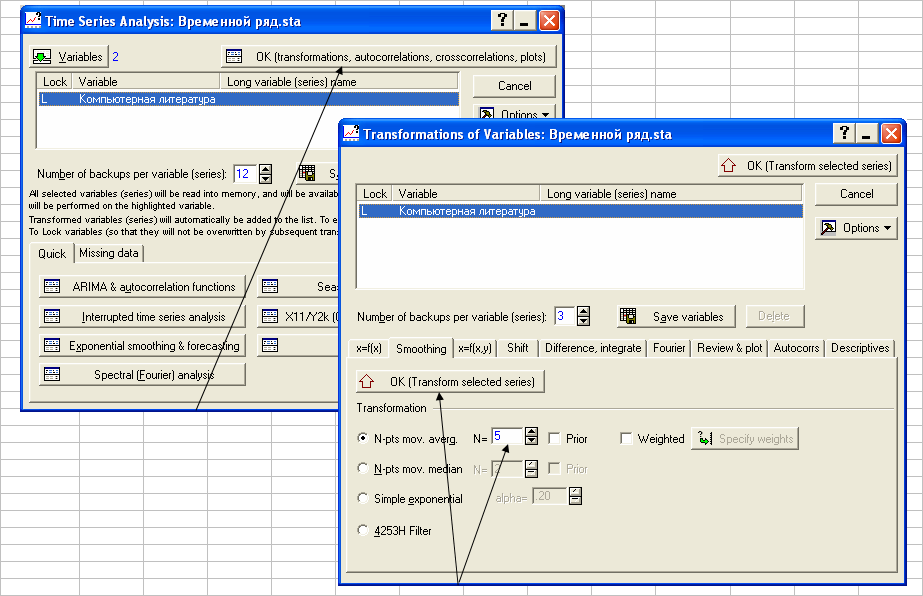
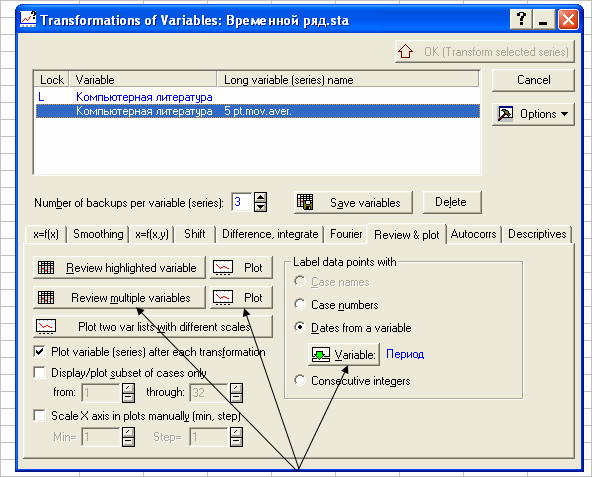
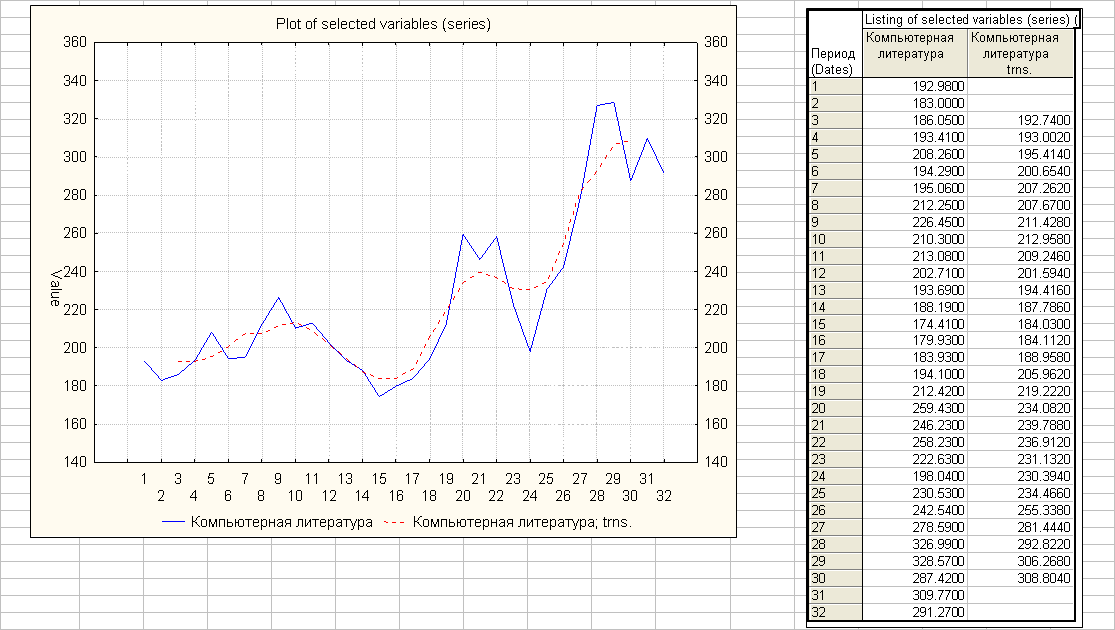
Сглаженные значения совпадают с результатами применения пакета "Анализ данных", но привязываются к средней точке окна сглаживания.

Сглаживание скользящей средней с использованием аппроксимирующего полинома (m=2, p=2, окно сглаживания L=2m+1=5)

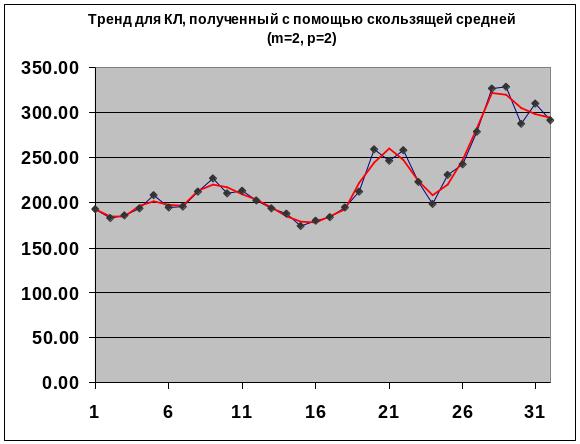
При данном методе структура сглаженного тренда в большей степени соответствует структуре исходного ряда и уменьшаются ошибки сглаживания по сравнения с использованием простой скользящей средней.

Метод экспоненциального сглаживания

Сглаживание с использованием пакета "Анализ данных" ( = 0.3)

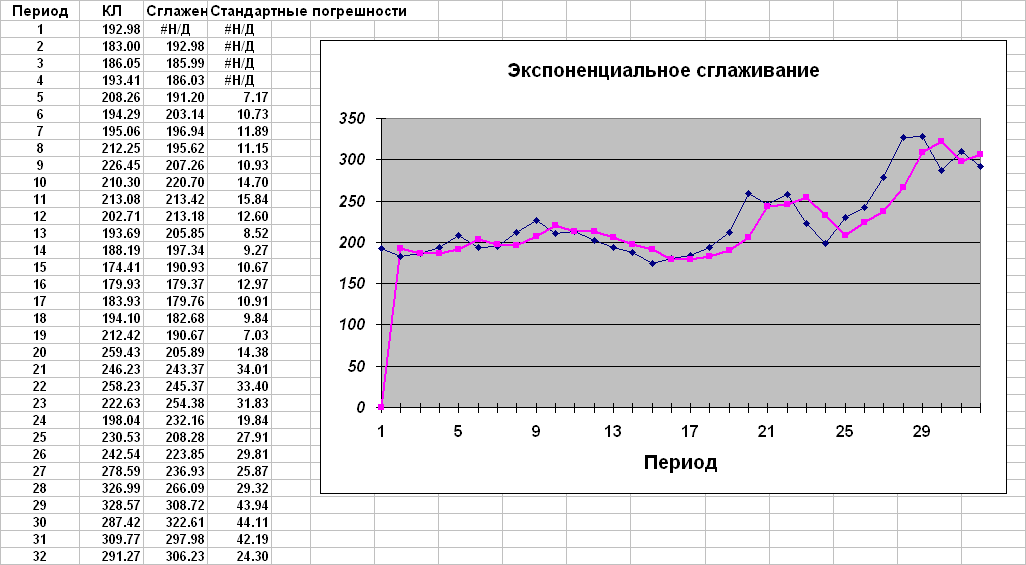
Сглаживание с использованием пакета "Анализ данных" ( = 0.3)

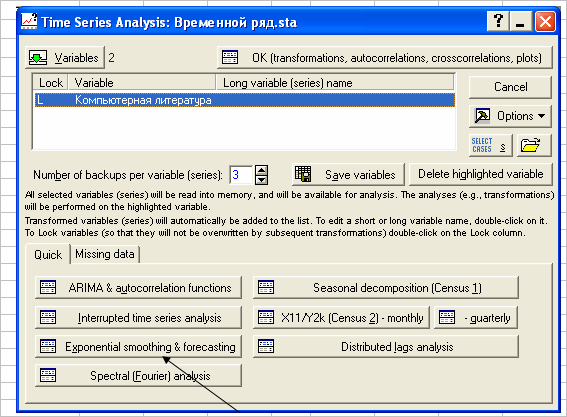
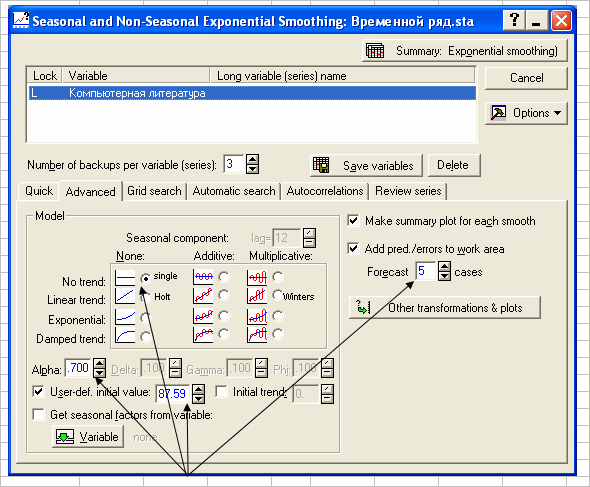
Если установлена опция No trend (тренд отсутствует), то выполняется простое экспоненциальное сглаживание. Если установлена опция Linear trend (линейный тренд), то применяется метод Брауна. Параметр  = 1 - , где  - фактор затухания, используемый в пакете "Анализ данных". Начальное сглаженное значение принимается равным начальному значению временного ряда.

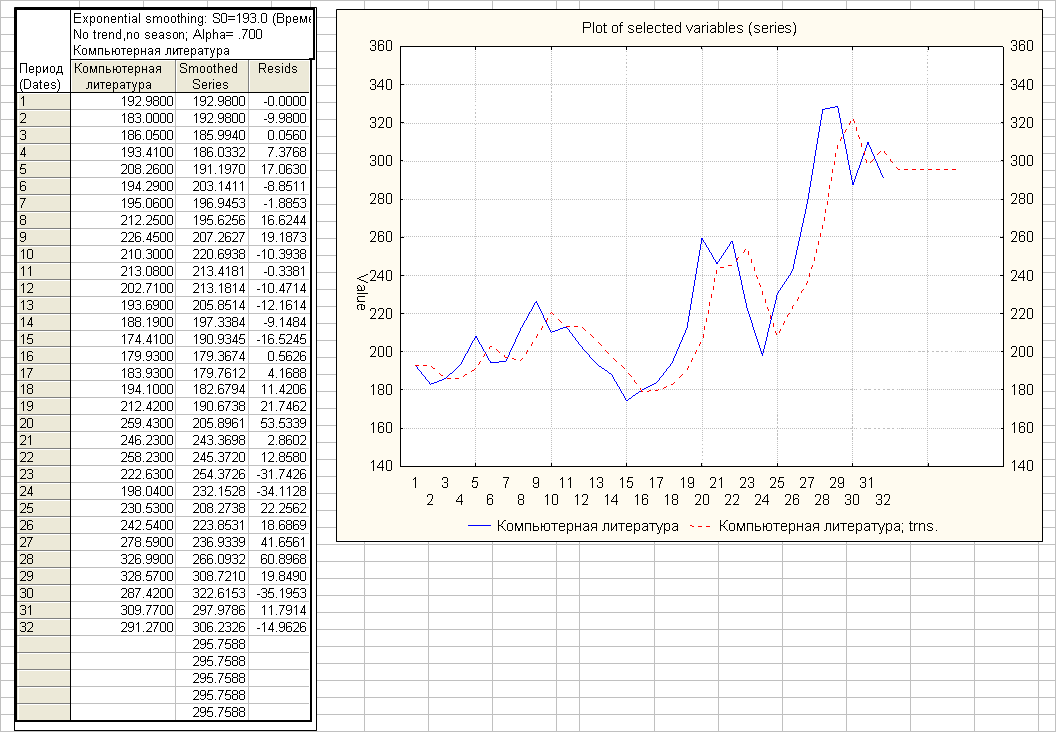
Сглаженные значения, полученные с использованием пакетов "Анализ данных" и STATISTICA, совпадают.

При увеличении  (уменьшении ) увеличивается значимость прошлых наблюдений, тренд становится более гладким.

Адаптивный метод Брауна

При краткосрочном прогнозировании наиболее важным является не тенденция развития исследуемого процесса, сложившаяся в среднем на всем периоде наблюдения, а его последние реализации. Свойство динамичности экономического процесса здесь преобладает над свойством его инерционности. Поэтому при краткосрочном прогнозировании может оказаться эффективным адаптивный метод Брауна, учитывающий неравноценность уровней временного ряда и обеспечивающий приспосабливаемость параметров модели к изменяющимся условиям.

В модели Брауна расчетное значение уровня ряда в момент t вычисляется по формуле:

Y_р(t) = a₀(t – 1) + a₁(t – 1) * k ,

где k – количество шагов прогнозирования, используемое при построении модели (обычно k = 1).

Расчетное значение сравнивается с фактическим уровнем ряда. Полученная ошибка прогноза (t) = Y(t) - Y_р(t) используется для корректировки модели по формулам:

a₀(t) = a₀(t – 1) + a₁(t – 1) +  (t) * (1 –²),

a₁(t) = a₁(t – 1) +  (t) * (1 – )² ,

где  – коэффициент дисконтирования данных, отражающий более высокую степень доверия к более поздним данным. Его значение должно быть в интервале от 0 до 1.

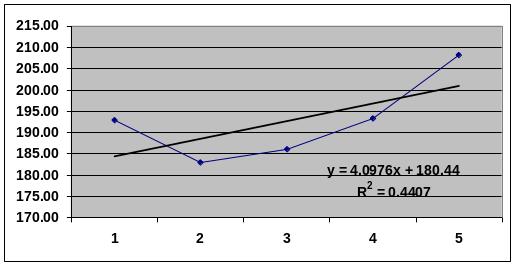
Начальные оценки параметров модели можно получить по первым пяти точкам при помощи МНК.

Результаты построения модели Брауна для ряда Компьютерная литература

Оценка начальных параметров модели МНК по первым пяти точкам

Результаты вычислений

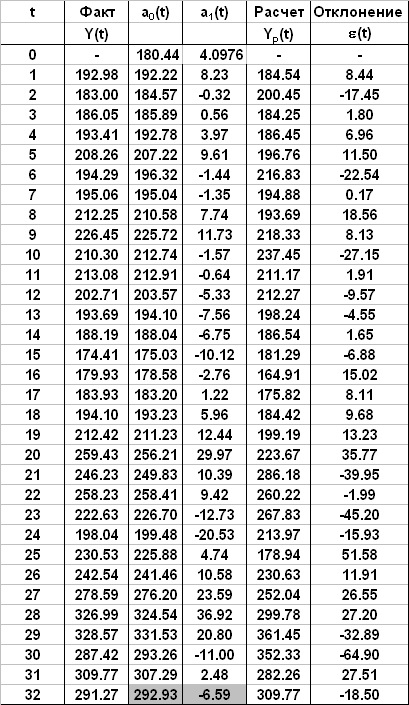
При прогнозировании используется модель, построенная на последнем шаге y(32+k) = 292.93 - 6.59*k