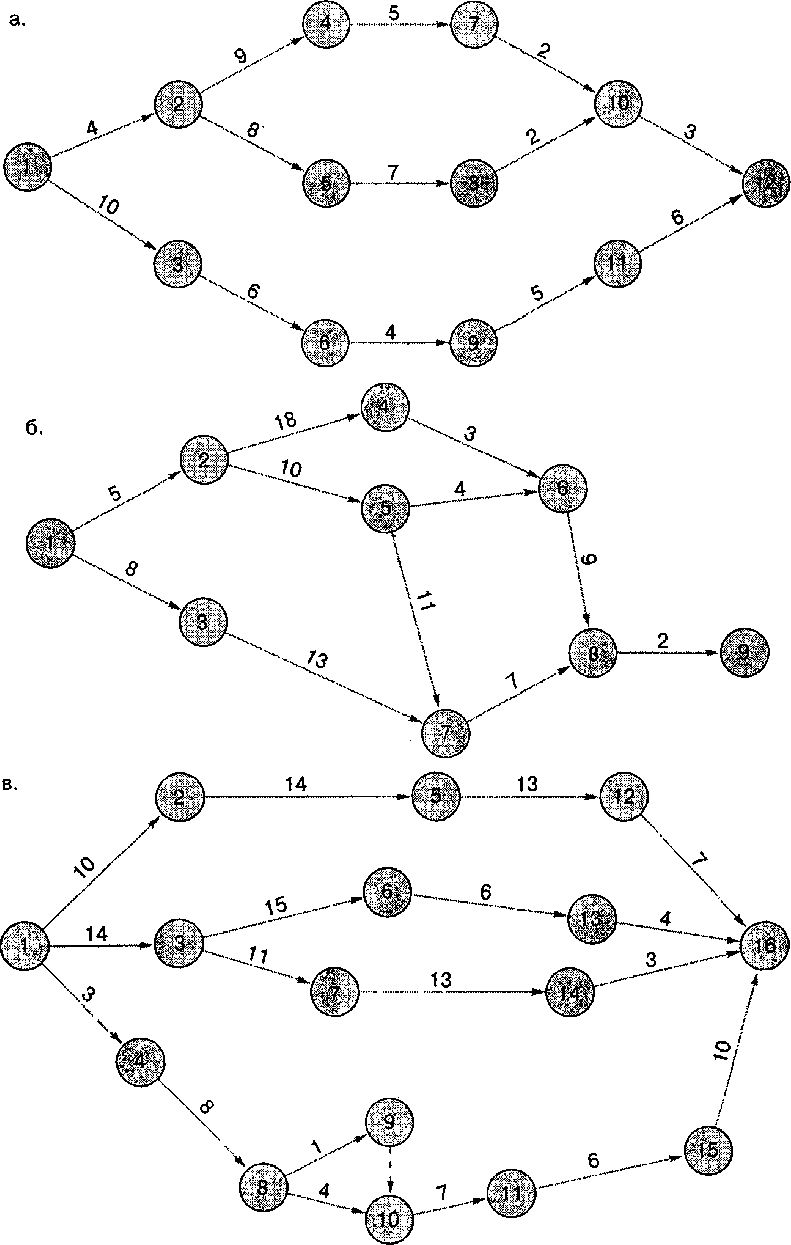
- •Пооперационный перечень работ.
- •Планирование с помощью диаграмм Гантта
- •Методы сетевого планирования pert и срм
- •Основы построения сетевых диаграмм
- •4.1. Сетевая диаграмма
- •Основные виды построений в сетевой диаграмме
- •Показатели времени в сетевой диаграмме. Расчет критического пути и резервного времени.
- •Принципы ускорения проектов путем привлечения дополнительных ресурсов.
Принципы ускорения проектов путем привлечения дополнительных ресурсов.
Оценки времени действий в проекте обычно даются для определенного уровня ресурсов. Во многих случаях бывает, возможно, сократить продолжительность проекта, введя дополнительные ресурсы. Мотивы для сокращения продолжительности проекта бывают разные: избежать убытков и штрафов за задержку, воспользоваться преимуществами денежно-кредитного стимулирования за своевременное или досрочное завершение проекта, или освободить ресурсы для использования в других проектах. При разработке нового изделия, сокращение сроков дает стратегическое преимущество: выиграть соревнование за рынок сбыта. В некоторых случаях, однако, желание сократить длительность проекта — это просто желание уменьшить косвенные расходы, связанные с работой проекта (например, расходы на мощности и оборудование, руководство и контроль, стоимость труда и заработную плату персонала). Часто руководитель проекта может выбирать из нескольких способов сократить определенные действия в проекте.
Самый простой способ - использовать дополнительные фонды, чтобы содержать дополнительный персонал или более эффективное оборудование, или «смягчить» некоторые слишком строгие спецификации. Следовательно, руководитель проекта может сократить длительность проекта, увеличивая прямые расходы, чтобы ускорить проект и, таким образом, сэкономить на косвенных расходах. Основная задача в оценке соотношения затрат и времени — определить путь, который даст минимальную сумму прямых и косвенных расходов по проекту.
Для того чтобы рационально выбрать, какие действия можно сократить (если вообще это возможно) и в какой степени их сокращать, менеджеру нужна определенная информация:
Оценки нормального и ускоренного времени для каждого действия.
Оценки расходов в случае нормального хода каждого действия и в случае его ускорения.
Список действий на критическом пути.
Действия на критическом пути — это потенциальные кандидаты для ускорения, так как ускорение некритических действий не повлияет на общую продолжительность проекта. С экономической точки зрения, действия нужно ускорять в соответствии с необходимыми для этого затратами: вначале ускорять там, где это дешевле всего обойдется. Кроме того, ускорение должно продолжиться до тех пор, пока затраты на ускорение остаются меньше, чем выгоды от этого ускорения. Эти выгоды могут принимать форму поощрительных выплат за досрочное завершение проекта, как часть правительственного контракта, или же они представляют собой экономию на косвенных расходах проекта, или и то и другое вместе. На рисунке 16-7 показана основная связь между косвенными, прямыми и общими расходами проекта, а также общая стоимость проекта при ускорении.
Общая процедура для ускорения:
Получить оценки регулярного и ускоренного времени и соответствующие затраты для каждого действия.
Определить длительность всех путей и их резервное время.
Определить, какие действия являются критическими.
Сократить критические действия, в порядке, который определен расходами на сокращение: сокращение с наименьшими расходами производится первым. Продолжать сокращение до тех пор, пока расходы на сокращение не превысят выгоды от сокращения. Обратите внимание на то, что при сокращении
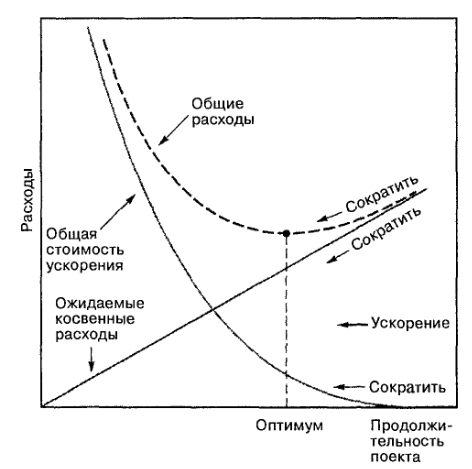
Ускоренные действия уменьшают косвенные расходы проекта и увеличивают прямые расходы; оптимальный результат ускорения — минимизация суммы этих двух типов расходов начального критического пути, «критичность» может смещаться — другие пути станут критическими. Следовательно, дальнейшие усовершенствования потребуют одновременного сокращения двух или более путей. В ряде случаев, самый разумный и экономически выгодный способ — сокращать действие, которое находится одновременно на двух (или более) критических путях.
ПРИМЕР 7
Используя следующую информацию, разработайте оптимальное соотношение затрат и времени. Примите, что косвенные расходы проекта составляют $1000 в день.
Действие |
Нормальное время |
Сокращенное время |
Стоимость сокращения ($ в день) |
а |
6 |
6 |
- |
Ь |
10 |
8 |
500 |
с |
5 |
4 |
300 |
d |
4 |
1 |
700 |
е |
9 |
7 |
600 |
f |
2 |
1 |
800 |
Решение:
а. Определите, какие действия находятся на критическом пути, длину критического пути и длину второго пути:
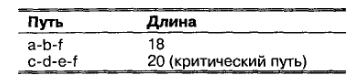
б. Распределите действия критического пути в порядке наименьших затрат на ускорение и определите число дней, на которое можно сократить каждое действие.

в. Начните сокращать проект, по одному дню за один раз, и одновременно проверяйте после каждого сокращения, какой путь является критическим. (В определенный момент, второй путь может стать равным длине сокращенного критического пути.) Таким образом:
(1) Сократите действие с на один день. Это обойдется в $300. Длина критического пути стала 19 дней.
(2) Действие с не поддается дальнейшему сокращению. Сокращаем действие е на один день. Это стоит $600. Длина пути с-d-е-f становится 18 дней, т.е. она теперь равна длине пути а-d-f.
(3) Поскольку оба пути теперь являются критическими, дальнейшие усовершествования будут требовать ускорения одного действия на каждом. Оставшиеся действия для ускорения и стоимость ускорения:
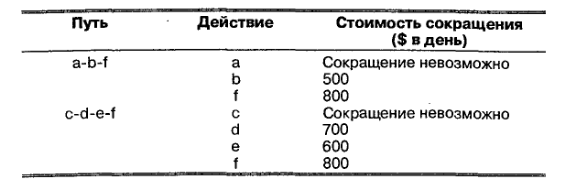
На первый взгляд, кажется, что ускорять действие т будет невыгодно, потому что здесь самая высокая стоимость ускорения. Однако действие f находится на обоих путях — значит, сокращение f на один день сократит оба пути (и следовательно, проект) на один день при затратах $800. Вариант сокращения наименее дорогого действия на каждом пути будет стоить $500 для Ь и $600 для е, или всего $1100. Таким образом, сокращаем f на один день. Теперь продолжительность проекта — 17 дней.
На данном этапе никакое дополнительное усовершенствование невозможно. Расходы на ускорение Ь — $500; расходы на ускорение е — $600, на общую сумму $1100. Это превысит ежедневные расходы по проекту ($1000 в день).
Последовательность ускорений приведена ниже:

Преимущества и ограничения метода PERT
PERT и подобные ему методы планирования проектов могут оказать большую помощь руководителю проекта. Приведем некоторые наиболее полезные возможности метода:
Использование этого метода позволяет руководителю проекта организовать и рассчитать количественные показатели по всей доступной ему информации, а также определить, где необходима дополнительная информация.
Методы обеспечивают графическое отображение проекта и его главных действий.
Они выявляют (а) действия, за которыми нужен пристальный контроль, так как они могут задержать весь проект, и (б) другие действия, которые имеют резервное время и поэтому их задержка не скажется на общем времени проекта. Это открывает возможность для перераспределения ресурсов и сокращения проекта.
Ни один аналитический метод не бывает без ограничений. Среди наиболее важных ограничений PERT следующие:
При разработке сетевой диаграммы проекта одно или более важных действий может быть пропущено.
Связи и последовательность действий не всегда бывают точно отображены.
Оценки времени могут включать мнимые факторы; менеджеры стараются избежать необходимости оценивать временные параметры проекта, потому что они обычно заранее настроены на завершение проекта в определенные сроки.
Решение задач
Задача 1
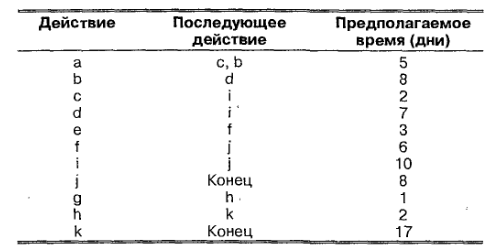
Следующая таблица содержит информацию о главных действиях исследовательского проекта. Используйте эту информацию, чтобы сделать следующее:
а. Составить диаграмму предшествования.
б. Найдите критический путь.
в. Определите ожидаемую продолжительность проекта.
Решение:
а. При построении сетей могут быть полезны следующие наблюдения:
Действия, у которых нет предшественников, располагаются в начале сети (левая сторона).
Действия с несколькими предшествующими размещены на пересечениях пути. Начните сетевую диаграмму с определения всех действий без предшественников:
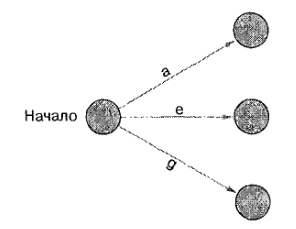
Затем последовательно завершите диаграмму. Пройдите сверху вниз список действий, чтобы ни одно не пропустить. Этот процесс показан на следующей диаграмме.

Вот несколько дополнительных подсказок для построения диаграммы предшествования:
Пользуйтесь карандашом.
В начале и конце диаграммы должен быть один узел.
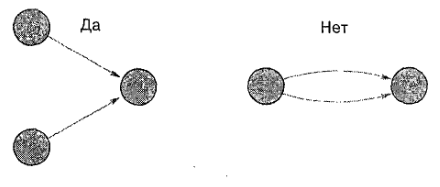
Избегайте пересечения путей.
Нумеруйте узлы слева направо.
Направляйте действия слева направо.
Используйте только одну стрелку между любой парой узлов.

Задача 2
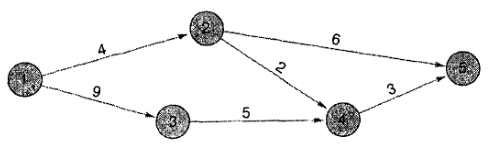
Используя алгоритм вычисления, определите резервное время для следующей диаграммы. Определите действия, которые находятся на критическом пути.
Решение:
Определение времени ES, ЕF, LS и LF можно значительно упростить, установив две скобки для каждого действия, как это показано ниже:
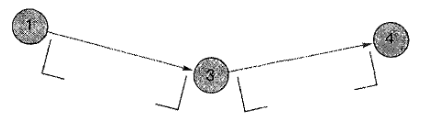
Левая скобка для каждого действия будет заполнена самым ранним и самым поздним начальным временем, а правая скобка для каждого действия будет заполнена самым ранним и самым поздним конечным временем:

Все это выполняется в два этапа. Сначала определяем самое раннее начальное и самое раннее конечное время, действуя слева направо, как показано в следующей диаграмме.
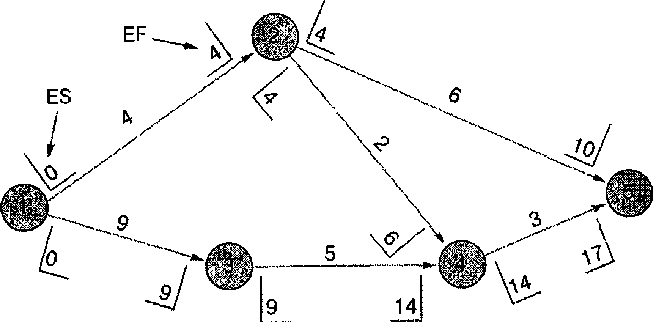
Таким образом, 0 — это начало действия 1-2. Со временем действия=4, это действие может быть закончено в 0+4=4. Это устанавливает самое раннее начальное время для всех действий, которые начинаются в узле 2. Следовательно, 2-5 и 2-4 могут начаться не ранее, чем время 4. Действие 2-5 имеет раннее время окончания 4+6=10, а действие 2-4 имеет раннее время окончания 4+2=6. На данном этапе невозможно сказать, каким будет самое раннее начало для действия 4-5: это будет зависеть от того, какое действие — 3-4 или 2-4 — имеет более позднее ЕF. Следовательно, необходимо вычислить ЕS и ЕF по нижнему пути. При ES=0 для действия 1-3, его ЕF=9, поэтому действие 3-4 будет иметь ES=9 и ЕF=9+5=14. Учитывая, что два действия, входящие в узел 4, имеют время ЕF соответственно 6 и 14, самый ранний момент, когда может начаться действие 4-5, равен большему из этих значений, т.е 14. Следовательно, действие 4-5 имеет ES=14 и EF=14+3=17. Теперь сравним время ЕF действий, входящих в конечный узел. Самое большее из них 17. Это ожидаемая продолжительность проекта.
Теперь можно определить время LFи 13 для каждого действия, двигаясь назад по сети (справа налево). LFдля двух действий, входящих в узел 5, будет равно 17, т.е. продолжительности проекта. Другими словами, для завершения проекта через 17 недель, эти последние два действия должны закончиться к этому сроку. В случае действия 4-5 1_3, необходимое, чтобы 1_Р=17, будет 17-3=14. Это значит, что действия 2-4 и 3-4 должны закончиться не позже, чем через 14 недель. Следовательно, их время 1_Р=14. Действие 3 имеет время 1.5=14-5=9, при этом для действия 1-3 1_Р=9 и 1.5=9-9=0.
Действие 2-4, с временем LF=14, имеет время LS=14-2=12. Действие 2-5 имеет LF=17 и, следовательно, LS=17-6=11. Таким образом, самый поздний срок для начала действия 2-5 LS=11, и для действия 2-4 LS=12, чтобы эти действия закончились к 17 неделе. Так как действие 1-2 предшествует обоим этим действиям, то оно должно закончиться не позже, чем меньший из этих показателей, т.е. 11. Следовательно, действие 1-2 имеет LF=11 и LS=11-4=7. Времена ЕS, EF, LF и LS показаны на следующей диаграмме.
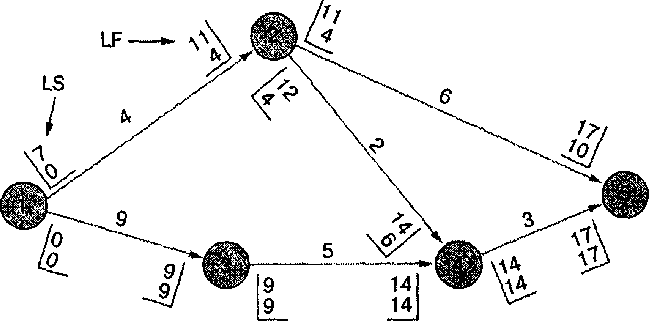
Действие |
LS |
ES |
Резерв или LF |
EF |
Резерв |
|
1-2 |
7 |
0 |
7 |
11 |
4 |
7 |
2-5 |
11 |
4 |
7 |
17 |
10 |
7 |
2-4 |
12 |
4 |
8 |
14 |
6 |
8 |
1-3 |
0 |
0 |
0 |
9 |
9 |
0 |
3-4 |
9 |
9 |
0 |
14 |
14 |
0 |
4-5 |
14 |
14 |
0 |
17 |
17 |
0 |
Действия с нулевым резервным временем указывают на критический путь. В этом
случае критический путь 1 -3-4-5.
При работе с подобными задачами имейте в виду следующее:
а. Время ЕS для действий, выходящих из узлов с многими входящими действиями, является наибольшим EF для входящих действий.
б. Время LF для действий, входящих в узлы со многими выходящими действиями, является наименьшим LS для выходящих действий.
Задача 4
Косвенные затраты для проекта — $12000 в неделю на всем этапе выполнения. Руководитель проекта установил показатели времени и расходов, информация о которых представлена в таблице. Используйте эту информацию, чтобы:
а. Определить оптимальный план ускорения.
б. Отобразить графически общие расходы для этого плана.


Решение:
а. (1) Рассчитайте длину путей и определите критический путь:

(2) Распределите критические действия по расходам на сокращение:

Действие Ь нужно сократить на одну неделю, так как с ним связаны меньшие расходы на сокращение. Это уменьшит косвенные расходы на $12000, что обойдется в $3000 — с чистой экономией $9000. На этом этапе оба пути а-Ь и е-f имеют длину по 23 недели, поэтому оба они будут критическими.
(3) Распределите действия на двух критических путях в соответствии со стоимостью сокращения:

На каждом пути выберите одно действие (наименее дорогостоящее) для сокращения: действие Ь на пути а-Ь и действие 1 на пути е-*, на общую сумму затрат $4000 + $2000 = $6000 и чистой экономией средств $12000 - $6000 = $6000.
(4) Проверьте, какой путь (пути) будет критическим: длина а-b и е-f по 22 недели,
длина с-с1 по-прежнему 19 недель.
(5) Распределите действия на критических путях:

Сокращение действий Ь на пути а-Ь и е на пути е-1 обойдется в $4000 + $6000 = $10.000, при чистой экономии $12000 - $10000 = $2000.
(6) На данном этапе никакое дальнейшее усовершенствование невозможно: пути а-Ь и е-1 имеют продолжительность 21 неделю, и нужно было бы сократить по одному действию на каждом пути. Это означает действие а со стоимостью сокращения $11000 и действие е со стоимостью сокращения $6000 на общую сумму $17000. Эта сумма превышает $12000 потенциальной экономии на косвенных расходах.
б. Следующая таблица подводит итоги, показывая длительность проекта после сокращения п недель:
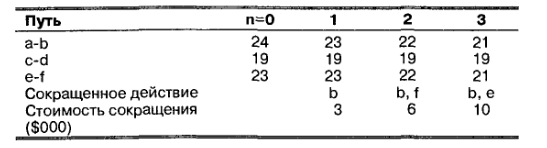
В результате мы имеем следующую картину расходов:

График общих расходов:
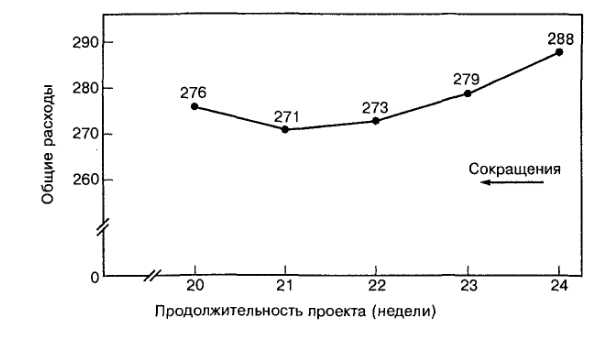
Задачи