2. Показатели времени в сетевой диаграмме. Расчет критического пути и резервного времени.

Лучший путь к пониманию природы сетевого ана­лиза— рассмотреть простой пример.

ПРИМЕР 1

Дана следующая информация: Рис.6

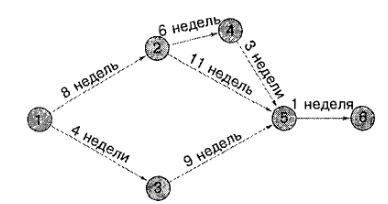
Определите:

а. Длину каждого пути

б. Критический путь

в. Ожидаемую продолжительность проекта.

г. Количество резервного времени для каждого пути.

Решение:

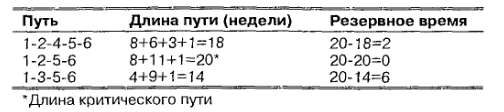
а. Как показано в следующей таблице, длина путей —18 недель, 20 недель и 14 недель.

б. Самый длинный путь (20 недель) — 1 -2-5-6, поэтому он — критический путь.

в. Ожидаемая продолжительность проекта равна длине критического пути (т.е. 20 недель).

г. Мы находим резерв времени для каждого пути, вычитая длину этого пути из длины критического пути, как это показано в последнем столбце таблицы. {Обратите внимание: иногда желательно знать резервное время для каждого действия. Следующий раздел описывает метод получения таких показателей.)

Алгоритм вычисления

Сетевые диаграммы многих реальных проектов намного больше, чем простая сеть, по­казанная в предшествующем примере; они часто содержат сотни и даже тысячи дейст­вий. Поскольку необходимые вычисления могут стать чрезвычайно сложными и по­требовать много времени, большие сетевые диаграммы, как правило, анализируются компьютерными программами, а не вручную. Интуитивный подход, показанный выше, не поддается компьютеризации, потому что во многих случаях последователь­ности путей не так легко распознать. Вместо этого, используют алгоритм для получе­ния четырех видов информации о действиях в сети:

ES, самое раннее время, когда действие может начаться, принимая, что все пред­шествующие действия начинаются насколько возможно раньше.

EF, самое раннее время, когда действие может быть законченно.

LS, самое позднее время (самый последний срок), когда действие может начаться, не задерживая проект.

LF, самое позднее время (самый последний срок), когда действие может закон­читься, не задерживая проект.

Когда эти значения определены, их можно использовать, чтобы найти:

1. Ожидаемую продолжительность проекта.

2. Резервное время.

3. Действия на критическом пути.

Три следующих примера показывают, как вычислить эти значения, используя диа­грамму предшествования примера 1.

Вычисление времени ES и ЕF

Вычислению самого раннего начального и конечного времени помогают два простых правила:

1. Самое раннее конечное время для любого действия равно его самому раннему начальному времени плюс его ожидаемая продолжительность t:

ЕF=ES-t

2. ES для действий в узлах с одной входящей стрелкой равно ЕF входящей стрел­ки. ES для действий, выходящих из узлов со многими входящим стрелками, равен самому большому ЕF входящей стрелки.

Нахождение времени ES и ЕР предполагает «шаг вперед» по сети

ПРИМЕР 2

Вычислите самое раннее начальное время и самое раннее конечное время для каждого действия в диаграмме, показанной на рисунке 16-4.

Решение:

Начнем с размещения скобок в обоих концах каждого начального действия:

Мы определяем и помещаем в скобки самое раннее начальное время для каждого действия ES, и самое раннее конечное время ЕF.

Проделайте это для всех действий, начиная с левой стороны диаграммы предшест­вования и перемещаясь в правую сторону.

Когда для действия определено ES, ЕР можно найти, сложив время действия 1 с ES: ES + t = ЕР.

Для всех начальных действий берите ES = 0. Таким образом, действиям 1-2 и 1-3 назначаются нулевые значения ES. Это позволяет вычислить ЕР для каждого из этих действий:

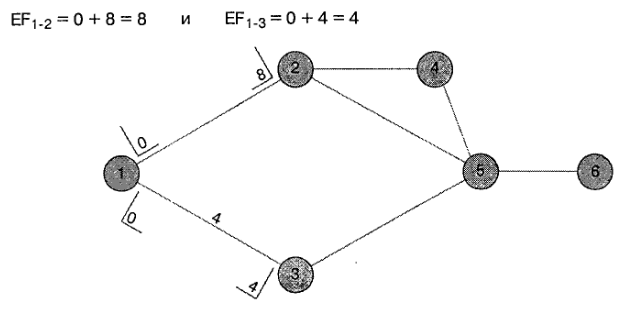
Время ЕР для одного действия становится временем ES для действия, которое следует за ним в диаграмме. Следовательно, поскольку у действия 1-2 время ЕР=8, то действия 2-4 и 2-5 имеют время ES тоже равное 8. Аналогично, у действия 3-5 время ES=4.

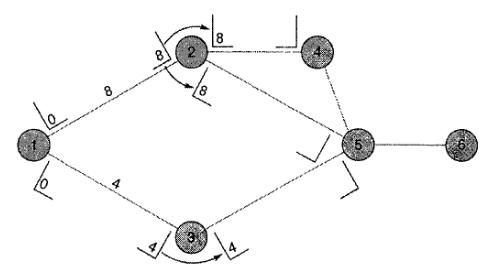
Это позволяет вычислить время ЕР для данных действий: ЕF₂.₄ = 8 + 6 = 14

ЕF₂.₅ = 8 + 11 = 19

ЕF₃.₅ = 4 + 9 = 13

Чтобы определить время ES для действия 5-6, мы должны помнить, что действие 5-6 не может начаться до тех пор, пока не закончено каждое предшествующее ему действие. Следовательно, самое большое из ЕF трех действий, которые предшествуют 1 действию 5-6, определяет ES для действия 5-6. Следовательно, ES для действия 5-6 будет 19.

Тогда ЕF для последнего действия (5-6) равно 20:

ЕF₅-₆ = 19+ 1 =20.

Обратите внимание, что последнее ЕF — это продолжительность проекта. Таким образом, ожидаемая длина проекта— 20 недель.

Вычисление времени LS и LF

Вычислению самого позднего начального и конечного времени помогают два правила:

1. Самое позднее начальное время для каждого действия равно его самому позд­нему конечному времени минус время продолжительности этого действия: LS=LF-1

2. Для узлов с одной выходящей стрелкой, LF для стрелок, входящих в этот узел, равно LS выходящей стрелки. Для узлов со многими выходящими стрелками, LF для стрелок, входящих в этот узел, равно наименьшему LS выходящих стрелок.

Нахождение време­ни LS и LF предполагает «шаг назад» по сети. Следовательно, мы должны начать с ЕР последнего действия и использовать это время как LF для последнего действия. Тогда мы получим Ь 8 для последнего действия, вычитая его ожидаемую продолжительность из его LF.

Вычислите самые поздние конечное и начальное время для диаграммы предшествования, показанной в примере 2.

Решение:

К скобкам на диаграмме нужно добавить время LS и LF.

Начинаем, приравнивая время LF последнего действия к его ЕР. Таким образом, LF_5-6 = ЕF_5-6 = 20 недель.

Получим время LS для действия 5-6, вычитая продолжительность действия t из вре­мени LF: LS₅-₆ = LF _5-б - t = 20 - 1 = 19.

Нанесите эти значения на диаграмму:

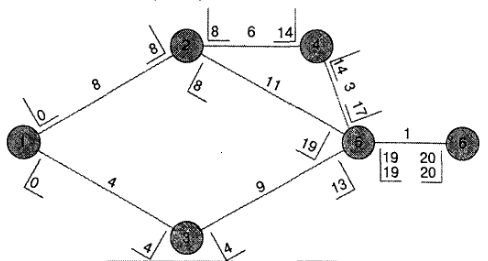
Время ES=19 для действия 5-6 становится теперь временем LF для каждого из дей­ствий, которые предшествуют действию 5-6. Это позволяет определить время LS для каждого из этих действий: вычтите продолжительность действия из LF, чтобы получить время LS для этого действия. Время LS для действия 3-5 : 19 - 9 = 10.

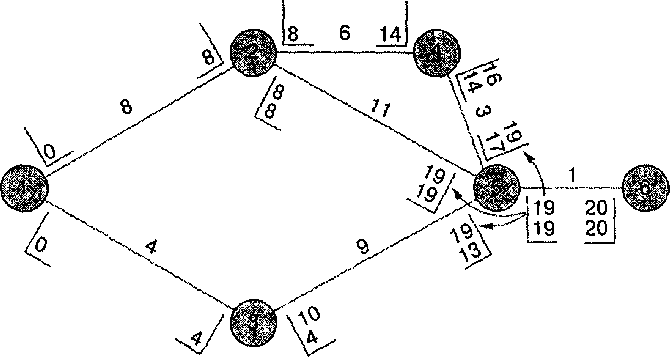
Затем, LS=16 действия 4-5 становится LF для действия 2-4, а LS=10 действия 3-5 становится 1Р для действия 1-3. Используя эти значения, находим LS для каждого из этих действий, вычитая продолжительность действия из времени LF.

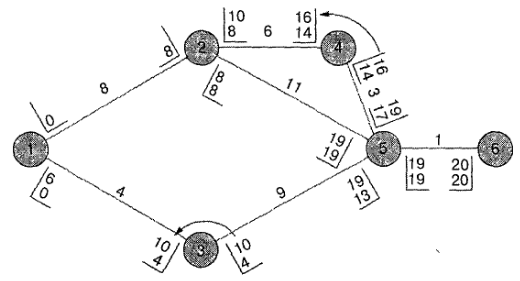
LF для действия 1 -2 является наименьшим из двух времен 13 предшествующих действий. Следовательно, время LF для действия 1-2 будет 8. Причина, почему мы используем наименьшее время, заключается в том, что действие 1-2 должно закончиться за время, которое позволит всем последующим действиям начаться не

позднее, чем их время 13.

Когда время LF действия 1 -2 определено, находим его время LS, вычитая продолжительность действия, равную 8, из времени LF, также равного 8. Следовательно, время LS =0.

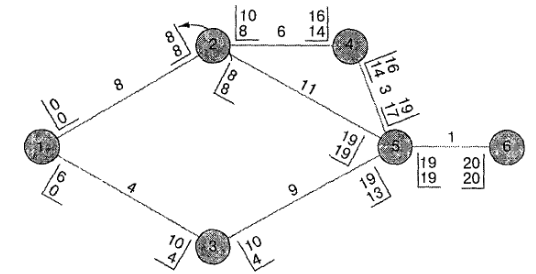
Вычисление резервного времени

Резервное время простоя можно вычислить двумя способами:

Резервное время = LS-ES или LF-ЕF (16-3)

Используя этот вычислительный алгоритм, критический путь обозначают дейст­виями с нулевым резервом времени. Так, таблица в примере 4 показывает, что дейст­вия 1-2, 2-5 и 5-6 все являются критическими, что соответствует результатам в приме­ре, которые были получены интуитивным методом.

Знание показателей резервного времени позволяет менеджеру точнее спланиро­вать распределение ограниченных ресурсов и направить деятельность по контролю на те действия, которые могут вызвать задержку в завершении проекта в срок. При этом точность решений будет выше, чем при более упрощенном интуитивном подходе. В этом отношении, важно помнить, что резервное время действия основано на предпо­сылке, что все действия на этом пути будут начаты как можно раньше и не превысят своей плановой продолжительности. Кроме того, если два действия на одном пути (на­пример, действия 2-4 и 4-5 в предыдущем примере) имеют одинаковый резерв времени (например, две недели), этот показатель будет обозначать общее (суммарное) резерв­ное время обоих действий. В сущности, действия на пути имеют общий временной ре­зерв. Следовательно, если первое действие использует весь резерв, для другого дейст­вия резерв будет нулевым. Настолько же уменьшится резерв и для всех остальных действий на этом пути.

ПРИМЕР 4

Рассчитайте резервное время для сетевой диаграммы на рис. 16-4.

Решение:

Вы можете использовать показатели начального времени или конечного времени. Предположим, мы выбираем начальное время. Используя время ЕЗ, вычисленное в примере 2, и время 1-8, вычисленное в примере 3, резервное время будет следую­щим:

Действие	LS	ES	(LS-ES) Резерв времени
1-2	0	0	0
1-3	6	0	6
2-4	10	8	2
2-5	8	8	0
3-5	10	4	6
4-5	16	14	2
5-6	19	19	0

Как отмечено выше, данный алгоритм поддается компьютеризации. Компьютер­ная распечатка для данной задачи будет примерно такой, как показано в таблице 16-1.