2. Основные виды построений в сетевой диаграмме

Построение и интерпретация сетевых диаграмм требует некоторого знакомства с сис­темой обозначений сетевых диаграмм. Их достаточно много, мы обсудим только некоторые самые важные и самые широкоупотребительные параметры сетевых диа­грамм. Этого будет достаточно, чтобы дать вам основу для понимания основных по­ложений, связанных с диаграммами предшествования, и позволит решать типичные задачи.

Одна из основных особенностей диаграммы предшествования—то, что она пока­зывает, какие действия должны выполняться последовательно (т.е. соблюдается усло­вие предшествования), а какие можно выполнять независимо друг от друга. Напри­мер, в приведенной ниже диаграмме, действие А должно быть завершено прежде, чем начнется действие В, и действие В должно быть завершено прежде, чем можно будет начать действие С.

Если диаграмма выглядит так, как показано ниже, оба действия А и В должны за­вершиться прежде, чем начнется действие С, но А и В могут выполняться одновремен­но; выполнение А не зависит от выполнения В.

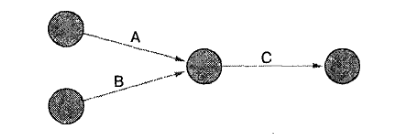
Если действие А должно предшествовать В и С, то соответствующая сетевая диа­грамма будет выглядеть следующим образом:

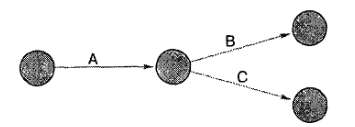
Когда в узловую точку входят несколько действий, то это значит, что все эти дей­ствия должны завершиться прежде, чем начнутся любые действия, которые начинают­ся в данном узле. Следовательно, в приведенной ниже диаграмме, действия А и В необ­ходимо закончить прежде, чем можно будет начать действия С или Б.

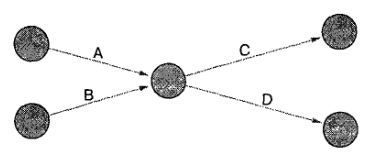
Когда два действия имеют одни и те же начальные и конечные узлы, используются фиктивный узел и действие, чтобы сохранить тождество каждого действия. В диаграм­ме, показанной ниже, действия А и В должны быть завершены прежде, чем будет нача­то действие С.

Тождества действий особенно важны для компьютерного анализа, потому что большинство компьютерных программ идентифицируют действия по их конечным точкам; действия с одними и теми же конечными точками могут быть неразличимы друг от друга, хотя они и имеют совершенно разные временные показатели.

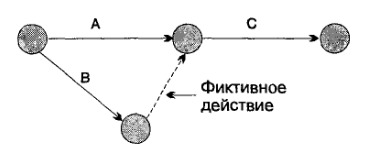
Фиктивные действия можно использовать различными способами. Еще один такой способ показан ниже:

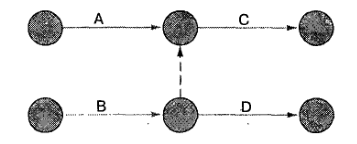
В данной ситуации действия А и В, оба должны предшествовать действию С. Од­нако начало действия Б зависит только от выполнения действия В и не зависит от вы­полнения А.

Основная функция фиктивного действия—прояснять взаимосвязи. В том, что ка­сается времени, фиктивное действие имеет нулевой показатель.

Для последующих ссылок, узловые точки нумеруются слева направо:

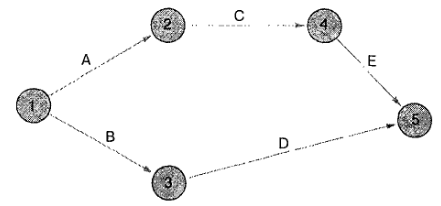
Иногда в процессе построения сетевой диаграммы, для большей наглядности, ис­пользуются стрелки, обозначающие начало и конец.

Диаграмма действия-в-узле

Альтернативный метод изображения сетевых диаграмм заключается в размещении действий в узлах (А-О-N), а не на стрелках. В результате получается диаграмма не­сколько другого вида. Различия можно оценить, сравнив два подхода к проблеме. Рас­смотрите следующий комплекс действий проекта:

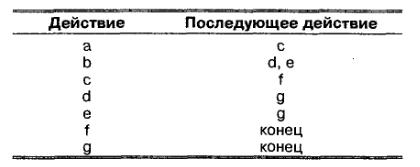
Рисунок 16-6 показывает оба типа сетей.

Одно очевидное различие в двух подходах заключается в том, что при подходе A-O-N в диаграмме получается больше узлов. Это общее правило. Второе различие — диаграмма А-О-А имеет фиктивную стрелку, которая нужна для того, чтобы правиль­но отобразить существующие отношения предшествования. Система A-O-N устраня­ет необходимость в фиктивных действиях. В этом состоит преимущество размещения действий в узлах.

На практике используются оба подхода. Большинство компьютерных программ для PERT/СРМ может работать с любой системой обозначений, но некоторые про­граммы требуют какой-либо определенной системы. Выбор метода часто зависит про­сто от личного предпочтения или традиций.

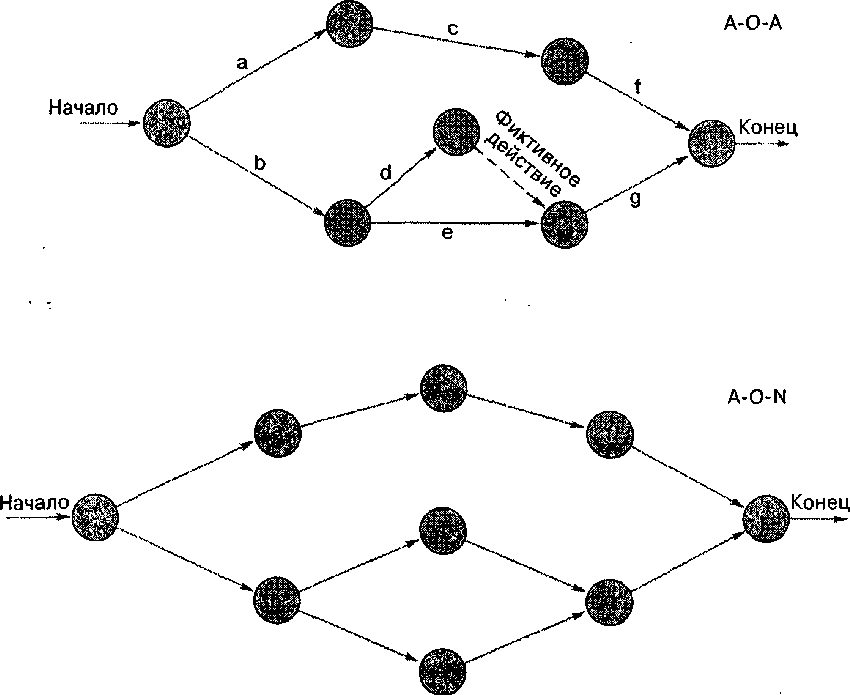
Рис. 16-6. Сравнение методов изображения сетей А-О-А и А-О-N