Реализация на эвм методов решения системы линейных алгебраических уравнений

В инженерной практике очень часто возникает необходимость в решении системы линейных алгебраических уравнений, например, при расчете электрических цепей постоянного и переменного тока.

Система линейных алгебраических уравнений имеет вид

,

, (4.5)

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

Для решения этой системы используются как точные, так и приближенные методы [1,2]. По коэффициентам системы (4.5) составляют расширенную матрицу

, (4.6)

которая является исходной для точных и приближенных методов.

Точные методы решения. Точные методы решения систем обычно основываются на исключении переменных (метод Гаусса) и состоят из двух этапов.

1 этап – исключение переменных.

Переменную х₁ исключают из 2,3,…, n-го уравнения. Переменную х₂ исключают из 3,4,…, n-го уравнения и т.д. Переменную х_n-1 исключают из n-го уравнения.

Для исключения, допустим переменной х_k из i-го уравнения, необходимо сначала определить множительный коэффициент как отношение элементов k-го столбца, расположенных в i-ой и k-ой строках. Далее каждый элемент i-ой строки изменяется путем вычитания соответствующего элемента k-ой строки, умноженного на коэффициент , т.е.

.

В результате таких преобразований элемент получит значение 0, а остальные элементы изменяются.

В процессе исключения переменных изменяются элементы расширенной матрицы (4.6), и она приобретает следующий вид:

, (4.7)

В квадратных скобках указано количество преобразований элементов расширенной матрицы. Элементы, стоящие на диагонали расширенной матрицы, являются главными; на эти элементы приходится делить при определении множительных коэффициентов. Чтобы не возникло ситуации деления на 0 или на очень маленькое число, что внесет большую погрешность в расчеты, анализируется главный элемент. Если он по абсолютной величине меньше некоторой величины е, то производится поиск другого элемента в k-ом столбце в строках от k+1 до n. Если такой элемент находится, допустим, в m-ой строке, то строки k-ая и m-ая меняются местами (происходит перестановка уравнений). При отсутствии элемента, пригодного в качестве главного в k-ом столбце, можно перейти к анализу элементов в k-ой строке, начиная с (k+1)-го столбца до n-го. Если такой элемент найден, допустим, в столбце m1, то меняются местами k и m1-ый столбцы (происходит перестановка переменных во всех уравнениях) и эти изменения заносятся в элементы массивов in1 и in2. Если этот поиск не увенчался успехом, то необходимо прекратить вычисления.

2 этап – нахождение корней системы.

По элементам последней строки матрицы (4.7) можно найти значение . Значение корня используется для нахождения значения по элементам (n-1)-ой строки матрицы (4.7) и т.д. Таким образом, значение k-го корня через элементы k-ой строки и найденные корни , ,…, будет найдено как

_.

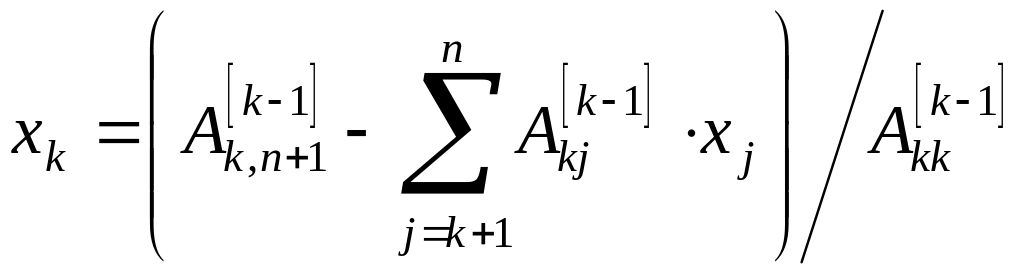Схема алгоритма метода Гаусса с поиском главного элемента по всей матрице приведена на рис. 4.1. В первой колонке организован ввод исходных данных, во второй реализован процесс исключения переменных, в третьей колонке показан этап поиска решения системы уравнений, в четвертой – печать результата и изменение индексов переменных, если это необходимо, в последней колонке отражен процесс поиска другого главного элемента в строках и столбцах матрицы.

Метод Гаусса используется в методе наименьших квадратов в качестве подпрограммы для определения и печати коэффициентов аппроксимации (см. рис. 4.3).

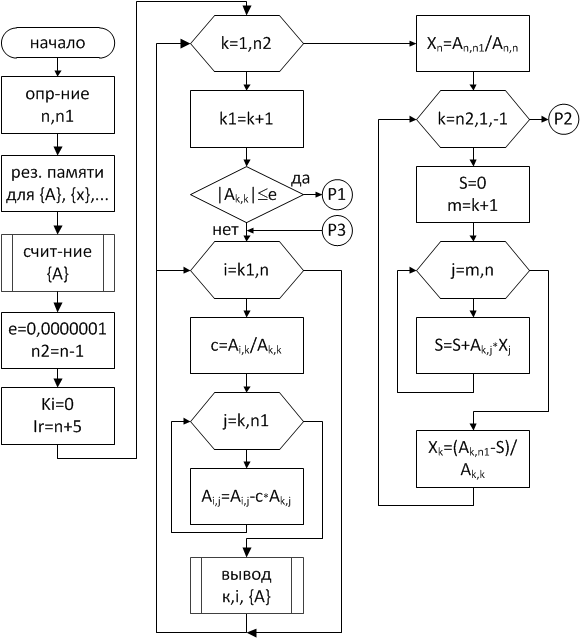
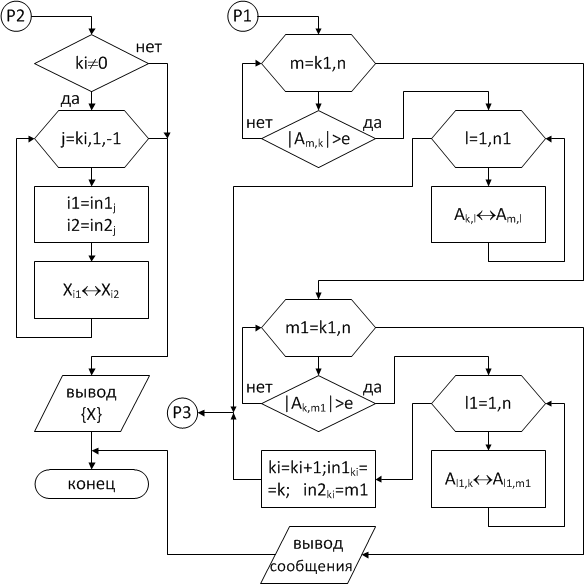
Рис. 4.1. Схема алгоритма решения системы линейных алгебраических уравнений