4. Аппроксимация полученного решения дифференциального уравнения 4-го порядка

Для исследования систем автоматического управления с нелинейными элементами, характеристики которых заданы в виде таблицы значений и моделирования таких характеристик на ЭВМ, приходится применять методы интерполяции или аппроксимации. Эти методы позволяют подобрать полином, описывающий нелинейную зависимость, представленную таблично.

Интерполяция – это подбор полинома m-ой степени, обеспечивающего прохождение функции через узловые точки. Количество узловых точек должно быть m+1.

Интерполяцию можно осуществить двумя способами:

1. подбирать один полином 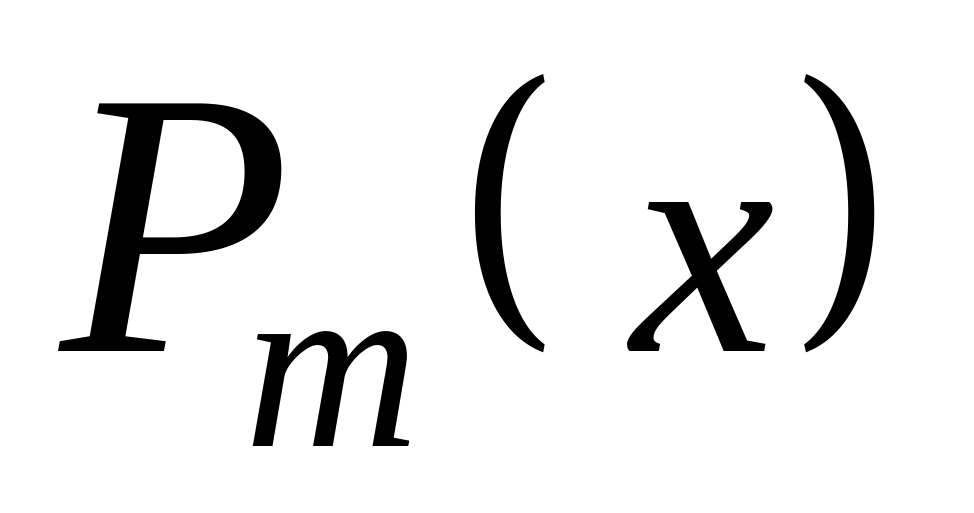для всей области определения аргумента х;

2. _{подбирать полином для каждого отдельного i-го участка (интерполяция сплайнами).}

Аппроксимация – это подбор полинома m-ой степени, обеспечивающего минимальное отклонение от узловых точек. Узловых точек в этом случае должно быть больше или равно m+1. В случае равенства будем иметь интерполяцию.

Аппроксимация методом наименьших квадратов

Полином, по которому аппроксимируется функция, заданная таблично, должен гарантировать минимум отклонения от табличных значений. Для этого среднеквадратичное отклонение 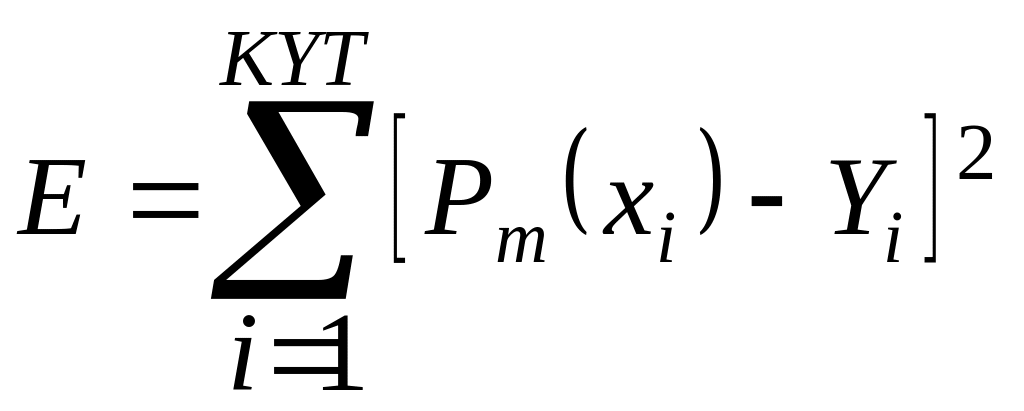должно быть минимальным.

Допустим, полином имеет вид

, (4.1)

где В_i – коэффициенты аппроксимации.

Для обеспечения минимума среднеквадратичного отклонения необходимо найти такие коэффициенты аппроксимации, которые обеспечили бы нулевые значения частным производным

.

Получим m+1 условие для определения всех коэффициентов:

,

,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,

.

Разделив уравнения на отдельные слагаемые, получим:

,

,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,

.

Вводя обозначения

и

, (4.2)

получим систему следующего вида:

,

,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . , (4.3)

.

Решив ее по методу Гаусса, определим значения коэффициентов аппроксимации.

Выражение (4.1) полинома для реализации на ЭВМ должно быть представлено в виде

_{. (4.4)}

Схема алгоритма аппроксимации по методу наименьших квадратов приведена на рис 4.2. В первой колонке осуществляется ввод исходных данных и производится вычисление коэффициентов и по формулам (4.2) с использованием координат узловых точек. В нижней части второй колонки готовятся данные для обращения к процедуре расчета системы линейных алгебраических уравнений (4.3) по методу Гаусса, а также производятся вычисление и печать коэффициентов аппроксимации по схеме алгоритма, приведенного на рис. 4.3. В третьей колонке вычисляются значения полинома , представленного выражением (4.4), для любых контрольных точек по схеме Горнера с использованием рекуррентной формулы

.

Интерполяцию плавно изменяющихся функций можно осуществлять по методу Лагранжа, Ньютона или Эйткена. Применение метода наименьших квадратов в этом случае дает более точные результаты на протяжении всего диапазона изменения аргумента, так как позволяет учесть все имеющиеся узловые точки при небольшой степени полинома.

При моделировании нелинейностей следует избегать участков с постоянными значениями функций, так как степенные полиномы между такими узлами формируют значения, сильно отличающиеся от требуемых; кроме того, в массив координат узловых точек обязательно нужно включать крайние точки области определения аргумента функции. Эти особенности следует учитывать при выборе метода интерполяции.