3.2. Решение уравнения состояния

Систему дифференциальных уравнений (3.1) можно представить как

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . , (3.3)

.

В матричном виде система (3.3) запишется следующим образом:

, (3.4)

или

, (3.5)

где Y – вектор координат состояния (Y_1,Y_2,…,Y_n); - вектор производных координат состояния; А – матрица состояния; F – вектор внешних воздействий.

Уравнения вида (3.4) и (3.5) принято называть уравнением состояния. Алгоритм решения уравнения состояния представлен на рис. 3.5. Схема алгоритма процедуры определения массива приращений {DY} в этом случае будет соответствовать рис. 3.6. Схемы же алгоритмов процедур, реализующих определение х, {Y} на каждом шаге интегрирования останутся прежними (см. рис. 3.2б, рис. 3.3а, рис. 3.3б, рис. 3.4).

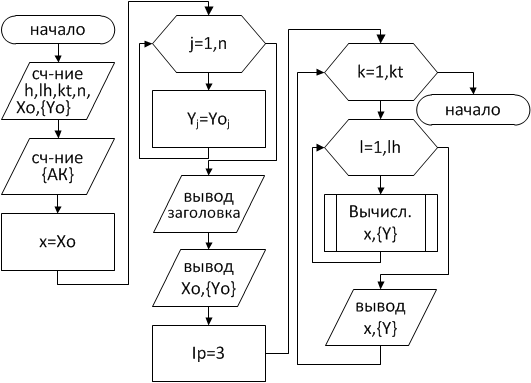
Рис. 3.5. Схема алгоритма решения уравнения состояния

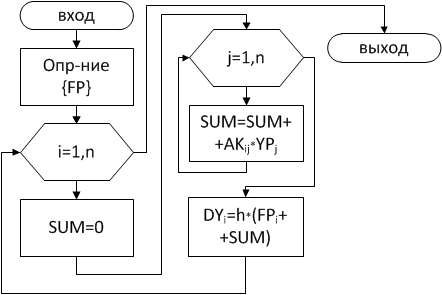
Рис. 3.6. Схема алгоритма процедуры определения {DY}

Для методов параллельного типа Пример 3.2. Найти решение уравнения состояния, соответствующего системе уравнений (3.2) из примера 3.1.

, , , .

Этой системе уравнений соответствует уравнение состояния вида

,

(3.6)

где .

Программа на языке VBA:

Option Explicit

Dim Y(1 To 10) As Single, DY(1 To 10) As Single

Dim YP(1 To 10) As Single, Ip As Integer, K As Integer

Dim S(1 To 10) As Single, Yo(1 To 10) As Single

Dim h As Single, Xo As Single, X As Single, Sum As Single

Dim n As Integer, i As Integer, j As Integer

Dim L As Integer, Kt As Integer, Lh As Integer

Dim AK(1 To 10, 1 To 10) As Single, FP(1 To 10) As Single

Private Sub CommandButton1_Click()

' ......................................................

' : Решение уравнения состояния по :

' : методу Эйлера (Эйлера-Коши, ломаных, Рунге-Кутта) :

' :....................................................:

h = TextBoxh: Lh = TextBoxLh: Kt = TextBoxKt

n = TextBoxKn: Xo = TextBoxXo

For j = 1 To n

Yo(j) = Cells(16, j + 5)

Next j

For i = 1 To n

For j = 1 To n

AK(i, j) = Cells(i + 6, j + 8)

Next j

Next i

X = Xo: For j = 1 To n: Y(j) = Yo(j): Next j

Cells(1, 1) = "Решение системы дифференциальных уравнений:"

Cells(2, 1) = " X"

For j = 1 To n

Cells(2, j + 1) = " Y(" & Str(j) & ")"

Next j:

Cells(3, 1) = Xo

For j = 1 To n

Cells(3, j + 1) = Yo(j)

Next j:

Ip = 3

For K = 1 To Kt

For L = 1 To Lh

' Call E

' Call EK

' Call RK2

Call RK4

Next L

Cells(Ip + K, 1) = X

For j = 1 To n

Cells(Ip + K, j + 1) = Y(j)

Next j:

Next K

End Sub

Sub ODY()'Процедура определения приращений DY

FP(1)=0: FP(2)=0: FP(3)=0: FP(4) = 200 * (1 - Exp(-4 * X))

For i = 1 To n

Sum = 0

For j = 1 To n

Sum = Sum + AK(i, j) * YP(j)

Next j

DY(i) = h * (Sum + FP(i))

Next i

End Sub

Sub E()'Процедура решения уравнений по методу Эйлера

For j = 1 To n: YP(j) = Y(j): Next j

Call ODY

X = X + h: For j = 1 To n: Y(j) = Y(j) + DY(j): Next j

End Sub

Sub EK()'Процедура решения уравнений по методу Эйлера-Коши

For j = 1 To n: YP(j) = Y(j): Next j

Call ODY

X = X + h / 2:

For j = 1 To n: YP(j) = Y(j) + DY(j) / 2: Next j

Call ODY

X = X + h / 2:

For j = 1 To n: Y(j) = Y(j) + DY(j): Next j

End Sub

Sub RK2()'Процедура решения уравнений по методу ломаных

' ( Рунге - Кутта 2 - го порядка )

For j = 1 To n: YP(j) = Y(j): Next j

Call ODY

For j = 1 To n: S(j) = DY(j): Next j

X = X + h:

For j = 1 To n: YP(j) = Y(j) + DY(j): Next j

Call ODY

For j = 1 To n: Y(j) = Y(j) + (S(j) + DY(j)) / 2:

Next j

End Sub

Sub RK4()'Процедура решения уравнений по методу Рунге-Кутта

' 4 - го порядка

For j = 1 To n: YP(j) = Y(j): Next j

Call ODY

For j = 1 To n: S(j) = DY(j): Next j

X = X + h / 2

For i = 1 To 2

For j = 1 To n: YP(j) = Y(j) + DY(j) / 2: Next j

Call ODY

For j = 1 To n: S(j) = S(j) + 2 * DY(j): Next j

Next i

X = X + h / 2:

For j = 1 To n: YP(j) = Y(j) + DY(j): Next j

Call ODY

For j = 1 To n: Y(j) = Y(j) + (S(j) + DY(j)) / 6:

Next j

End Sub

Результат выполнения программы: