2. Формирование системы дифференциальных уравнений 1-го порядка и уравнения состояния по заданному дифференциальному уравнению -го порядка
2.1. Формирование системы дифференциальных уравнений 1-го порядка по заданному дифференциальному уравнению -го порядка
Для решения дифференциального уравнения -го порядка
необходимо сформировать систему дифференциальных уравнений 1-го порядка путем введения следующих обозначений:
;
;
;
…………………………
.
Исходное уравнение представим системой дифференциальных уравнений 1-го порядка следующего вида:
………….
|
.
(2.1) |
,
,
,
.
Формирование системы уравнений для решения дифференциального уравнения 4-го порядка рассмотрим на примере 2.1.
Пример 2.1. Сформировать систему дифференциальных уравнений 1-го порядка, соответствующую дифференциальному уравнению 4-го порядка
.
Это уравнение должно быть преобразовано в систему дифференциальных уравнений 1-го порядка путем введения следующих обозначений:
;
;
;
.
Исходное уравнение представим системой дифференциальных уравнений 1-го порядка следующего вида:
, ,
|
(2.2) |
,
.
2.2. Формирование уравнения состояния по заданному дифференциальному уравнению -го порядка
Систему дифференциальных уравнений (2.1) можно представить как
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . , (2.3)
.
В матричном виде система (2.3) запишется следующим образом:
,
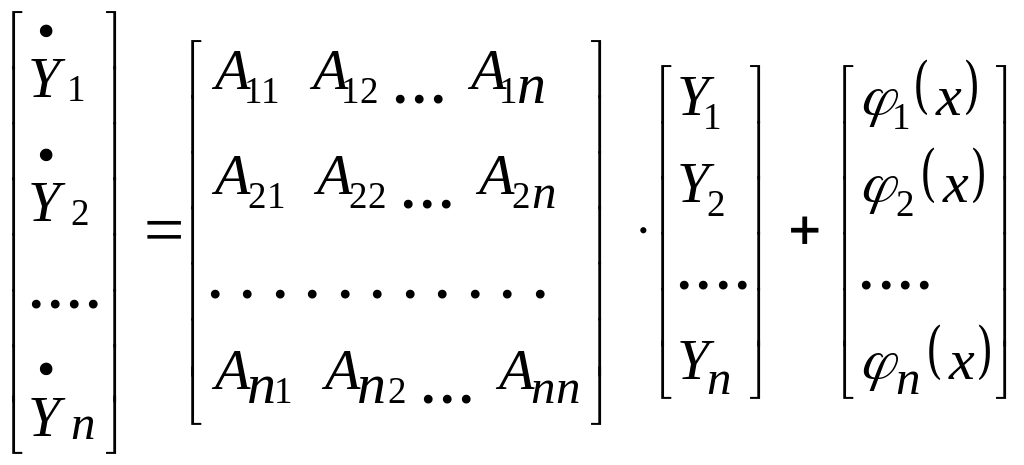(2.4)
или
(2.5)
где
Y
–
вектор координат состояния (Y1,Y2,…,Yn);
-
вектор производных координат состояния;
А
– матрица состояния; F
–
вектор внешних воздействий.
Формирование уравнения состояния для решения дифференциального уравнения 4-го порядка рассмотрим на примере 2.2.
Пример 2.2. Найти решение уравнения состояния, соответствующего системе уравнений (2.2) из примера 2.1.
, , , . |
|
Этой системе уравнений соответствует уравнение состояния вида
|
(2.6) |
,
где
.