Корней нелинейного уравнения Уточнение корней

Существует множество методов уточнения корней [1,2]. Наиболее распространенными являются: метод половинного деления, метод касательных (Ньютона) и метод итерации.

Метод половинного деления. Суть этого метода заключается в делении интервала между нижней и верхней границами существования корня пополам. Новое значение корня определяется как . Далее по произведению значений функции в двух точках определяют, на каком из двух отрезков находится корень и какую из границ нужно изменить, чтобы дальше делить отрезок, содержащий корень. Процедура деления продолжается до тех пор, пока полученные при делении отрезки не станут меньше заданной точности е. Геометрическая интерпретация и схема алгоритма приведены на рис.1.2.

Рис. 1.2. Схема и графическая интерпретация алгоритма уточнения

Корней по методу половинного деления

Метод касательных (Ньютона). Суть метода заключается в проведении касательной в текущей точке . Пересечение касательной с осью х дает новое, более точное значение , то есть , где - изменение аргумента, которое находится путем деления противолежащего катета на тангенс угла наклона касательной .

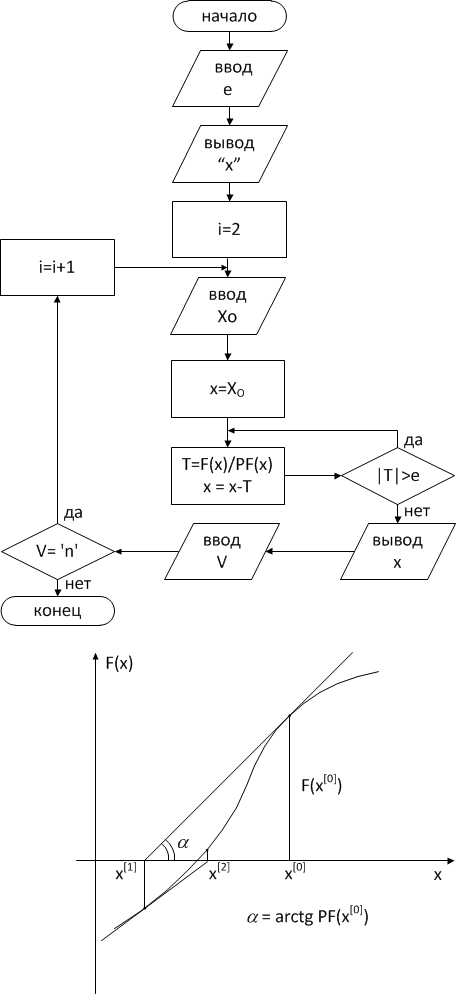
Рис. 1.3. Схема и графическая интерпретация алгоритма уточнения

Корней по методу Ньютона (касательных)

Этот процесс продолжается до тех пор, пока изменение аргумента Т не станет меньше заданной точности уточнения е, т.е. . Геометрическая интерпретация и схема алгоритма процесса уточнения приведены на рис.1.3.

Применяя рассмотренные выше алгоритмы и программы, можно отделить и уточнить только действительные корни.

Пример 1.1. По корням характеристического уравнения определить длительность переходного процесса , шаг интегрирования и шаг печати при количестве печатаемых точек , а также установившееся значение .

Неоднородное дифференциальное уравнение

Однородное дифференциальное уравнение

Характеристическое уравнение

или

или . (1.2)

_{Верхняя граница существования корней характеристического уравнения.}

_{Для определения этой границы используется уравнение (1.2) и формула Лагранжа (1.1). Так как отрицательных коэффициентов в уравнении (1.2) нет, то будем считать:}

_{Нижняя граница существования корней характеристического уравнения. Для определения этой границы используется уравнение}

или

_{и формула Лагранжа}

Для определения корней характеристического уравнения алгоритмы, приведенные на рис. 1.1 – рис. 1.3, следует объединить в одной программе по алгоритму, изображенному на рис. 1.4.

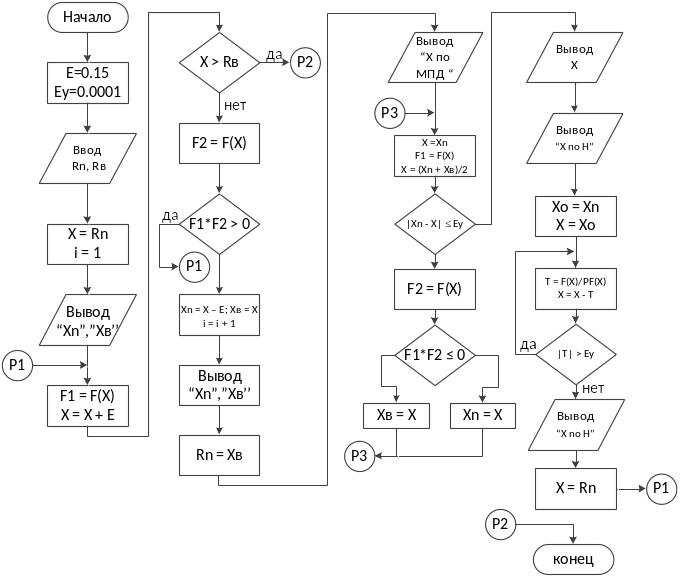
Рис. 1.4. Схема алгоритма программы отделения и уточнения корней

Нелинейного уравнения двумя методами

Листинг программы отделения и уточнения корней нелинейного уравнения двумя методами:

Private Sub CommandButton1_Click()

Dim X As Single, E As Single, Rn As Single, Rb As Single

Dim F1 As Single, F2 As Single, Xn As Single, Xb As Single

Dim Ey As Single, X0 As Single

Range("A1:E5").Clear

E = 0.12: Ey = 0.0001

Rn = InputBox("Введите Rn")

Rb = InputBox("Введите Rb")

X = Rn: i = 1:

Cells(1, 1) = " Pn": Cells(1, 2) = " Pb"

1: F1 = F(X)

X = X + E

If X > Rb Then GoTo 2

F2 = F(X)

If F1 * F2 > 0 Then GoTo 1

Xn = X - E: Xb = X: i = i + 1

Cells(i, 1) = Xn: Cells(i, 2) = Xb:

Rn = Xb

Cells(1, 3) = "Pi по МПД"

3: X = Xn: F1 = F(X): X = (Xn + Xb) / 2

If Abs(Xn - X) <= Ey Then

Cells(i, 3) = X

Else

F2 = F(X)

If F1 * F2 <= 0 Then Xb = X Else Xn = X

GoTo 3

End If

Cells(1, 4) = "Pi по Н-ну": Cells(1, 5) = "Ti=1/(-Pi)"

X0 = Xn

X = X0

4: T = F(X) / PF(X): X = X - T

If Abs(T) > Ey Then GoTo 4

Cells(i, 4) = X: Cells(i, 5) = 1 / (-X)

X = Rn: GoTo 1

2: End Sub

Function F(X As Single) As Single

F = X ^ 4 + 27 * X ^ 3 + 249 * X ^ 2 + 853 * X + 630

End Function

Function PF(X As Single) As Single

PF = 4 * X ^ 3 + 81 * X ^ 2 + 598 * X + 853

End Function

Результат выполнения программы:

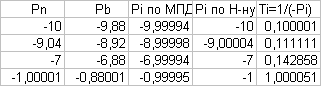
По максимальному и минимальному значениям определяем:

Длительность переходного процесса:

Шаг интегрирования: .

Если взять и , то шаг печати переходного процесса определится как .

Установившееся значение определяется из дифференциального уравнения ,

при и значениях производных, стремящихся к нулю

.

Установившееся значение равно .

Пример 1.2. Определить корни характеристического уравнения, не определенные в результате выполнения программы отделения и уточнения корней нелинейного уравнения.

Фрагмент программы отделения и уточнения корней нелинейного уравнения для уравнения :

Function F(X As Single) As Single

F = X ^ 4 + 16 * X ^ 3 + 93 * X ^ 2 + 230 * X + 200

End Function

Function PF(X As Single) As Single

PF = 4 * X ^ 3 + 48 * X ^ 2 + 186 * X + 230

End Function

Результат выполнения программы:

Из-за неточного представления целых чисел при преобразовании в вещественные получили только два корня .

Понижаем порядок уравнения

.

Корни уравнения равны .