1. Определение исходных данных для решения дифференциального уравнения -го порядка

Для решения дифференциального уравнения -го порядка требуется определить следующие исходные данные: длительность переходного процесса , шаг интегрирования и шаг печати по корням характеристического уравнения, а также установившееся значение по дифференциальному уравнению.

Формирование характеристического уравнения проводится в следующей последовательности:

Из неоднородного дифференциального уравнения -го порядка

, приравнивая нулю правую часть уравнения, получаем однородное дифференциальное уравнение

.

Применив к этому уравнению прямое преобразование Лапласа, получаем характеристическое уравнение

.

Характеристическое уравнение является разновидностью нелинейных уравнений и для нахождения корней этого уравнения необходимо применить численные методы решения.

1.1. Реализация на эвм методов решения нелинейных уравнений

Необходимость отыскания корней нелинейных уравнений встречается при расчетах линейных систем автоматического уравнения (для определения поведения системы в динамике), собственных колебаний машин и конструкций со многими степенями свободы и т.д. Основная форма записи этих уравнений .

Имеются две разновидности нелинейных уравнений: алгебраические и трансцендентные.

Алгебраические уравнения n-ой степени имеют n корней, коэффициенты могут быть как действительными, так и комплексными числами.

Трансцендентные уравнения содержат степенные, тригонометрические, экспоненциальные и другие функции от некоторого аргумента х, например, . Такие уравнения обычно имеют бесконечное множество корней.

Поиск корней нелинейного уравнения состоит из трех этапов [1, 2]: определение границ существования корней, отделение корней и уточнение корней.

Определение границ существования корней

Верхние и нижние границы существования корней алгебраического уравнения можно определить, используя формулу Лагранжа [1,2]:

, (1.1)

где – индекс первого из отрицательных коэффициентов полинома

;

– наибольшее из абсолютных значений отрицательных коэффициентов полинома .

Для использования формулы (1.1) необходимо, чтобы коэффициент был положительным ( ).

Для нахождения верхней границы существования положительных корней используется формула (1.1) для исходного уравнения . Для поиска других границ составляются вспомогательные уравнения.

Для поиска нижней границы существования положительных корней и верхней границы существования отрицательных корней используется уравнение вида . Эти границы определяются как , .

Для поиска нижней границы существования отрицательных корней используется вспомогательное уравнение вида , и эта граница определяется как .

Отделение корней

Все действительные корни нелинейного уравнения лежат на оси абсцисс. Отделение корней производится следующим образом [1,2]. Перемещаясь по оси х на величину шага поиска е от нижней границы существования корня до верхней , проверяем смену знака функции на каждом интервале. Находим такой интервал , на котором произошла смена знака функции или функция попала на ось ( ). Этот интервал и будет определять нижнюю и верхнюю границы существования одного из корней нелинейного уравнения. Смену знака определяют по произведению значений функций в двух соседних точках: и . Условие смены знака - . На рис.1.1 приведены графическая интерпретация и схема алгоритма поиска корней нелинейного уравнения. После определения и печати выделенного корня происходит возврат в начало алгоритма для отделения следующего корня. Этот процесс продолжается до достижения верхней границы существования корней.

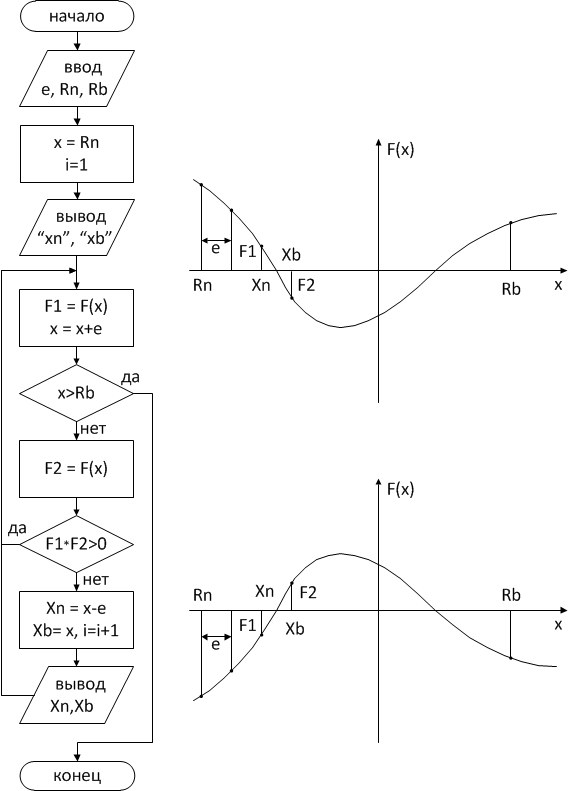
Рис. 1.1. Схема и графическая интерпретация алгоритма отделения