Лабораторная работа № 2 Изучение передачи информации с дискретным (цифровым) представлением сигналов

Цель работы: моделирование цифровой модуляции сигналов средствами пакета Matlab Communications Toolbox

Задание на выполнение работы:

1. Смоделировать цифровую амплитудную, фазовую и частотную манипуляции, приведенные в примерах 1,2,3.

2. Осуществить амплитудную, фазовую, частотную манипуляции и демодуляции заданного сигнала

Теоретические сведения

В настоящее время все большая часть информации, передаваемой по разнообразным каналам связи, существует в цифровом виде. Это означает, что передаче

подлежит не непрерывный (аналоговый) модулирующий сигнал, а последовательность целых чисел n₀, n₁, n₂, …, которые могут принимать значения из некоторого фиксированного конечного множества. Эти числа, называемые символами (symbol), поступают от источника информации с периодом T, а частота, соответствующая этому периоду, называется символьной скоростью (symbol rate): f_T = 1/T.

Замечание. Часто используемым на практике вариантом является двоичная (binary) последовательность символов, когда каждое из чисел n_i может принимать одно из двух значений — 0 или 1.

Последовательность передаваемых символов является, очевидно, дискретной. Поскольку символы принимают значения из конечного множества, то этот сигнал фактически является квантованным, т. е. его можно назвать цифровым сигналом. Далее будут рассматриваться вопросы, связанные с преобразованием этого цифрового сигнала в аналогов- модулированный сигнал.

Типичный подход при осуществлении передачи дискретной последовательности символов состоит в следующем. Каждому из возможных значений символа сопоставляется некоторый набор параметров несущего колебания. Эти параметры поддерживаются постоянными в течение интервала T, то есть до прихода следующего символа. Фактически это означает преобразование последовательности чисел {n_k} в ступенчатый сигнал s_n(t) с использованием кусочно-постоянной интерполяции:

s_n(t) = f(n_k), kT <=  t < (k + 1)T,

где f — некоторая функция преобразования.

Полученный сигнал s_n(t) далее используется в качестве модулирующего сигнала обычным способом. Такой способ модуляции, когда параметры несущего колебания меняются скачкообразно, называется манипуляцией (keying).

Рассмотрим на нескольких примерах моделирование канала с манипуляцией информационного параметра средствами пакета Matlab Communications Toolbox. Амплитудная манипуляция (АМн) осуществляется функциями dmod (формируется вещественный выходной сигнал) и dmodce (формируется комплексная огибающая) пакета Communications при указании в них параметра типа модуляции 'ask'. Следующий за ним параметр M указывает количество используемых уровней манипуляции. Символы, подлежащие передаче, должны принимать целочисленные значения, лежащие в диапазоне 0…M–1. Символу 0 соответствует значение амплитуды, равное –1, а символу M–1 — значение амплитуды, равное 1. Остальные уровни равномерно распределены между этими значениями. Таким образом, строго говоря, в данном случае может меняться не только амплитуда, но и фаза несущего колебания (отрицательные амплитудные множители соответствуют изменению фазы на 180°).

Пример 1. Обработка амплитудно- манипулированного сигнала

В качестве примера построим график сигнала, содержащего все возможные символы при 8-позиционной АМн. Его параметры:

M = 8; (количество уровней манипуляции)

sy = 0:M-1; (передаваемые символы)

Fd = 1; (символьная скорость)

Fc = 4; (несущая частота)

FsFd = 40; (отношение Fs/Fd)

Fs = Fd * FsFd; (частота дискретизации)

Формируем АМн-сигнал:

[s_ask, t] = dmod(sy, Fc, Fd, Fs, 'ask', M);

plot(t, s_ask)

grid on

На графике сигнала, изображенного на рисунке 1, хорошо виден бросок фазы в середине сигнала. Кроме того, можно заметить, что фазы посылок в первой и второй половинах сигнала, имеющих одинаковые амплитуды, отличаются на 180° .

Для осуществления амплитудной манипуляции реального сигнала его необходимо подвергнуть квантованию с помощью команды QUANTIZ . Синтаксис команды:

INDX = QUANTIZ(SIG, PARTITION)

Команда осуществляет квантование входного сигнала SIG, базируясь на решающих точках PARTITION. Каждый элемент в INDX является одним из N целых чисел в интервале [0: N-1]. PARTITION является строго возрастающим вектором порядка N-1, который определяет границы. Элементы INDX (0, 1, 2, ..., N-1) представляют SIG в диапазоне (-Inf, PARTITION(1)],(PARTITION(1), PARTITION(2)], (PARTITION(2), PARTITION(3)], ..., (PARTITION(N-1), Inf).

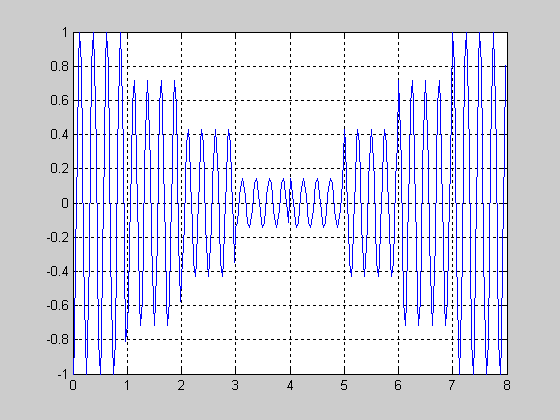
Рисунок 1 Амплитудно-манипулированный сигнал

Например, S=quantiz(s,0:0.1:0.5); Вектор количества уровней квантования должен иметь длину не больше М-1.

Демодуляция амплитудно-манипулированного сигнала осуществляется с помощью команды z = ddemod(y,Fc,Fd,Fs,'ask',M,);

Пример 2. Обработка фазо - манипулированного сигнала

Фазовая манипуляция осуществляется функциями dmod (формируется вещественный выходной сигнал) и dmodce (формируется комплексная огибающая) пакета Communications при указании в них параметра типа модуляции 'psk'. Следующий за ним параметр M указывает количество используемых градаций начальной фазы. Символы, подлежащие передаче, должны принимать целочисленные значения, лежащие в диапазоне 0…M–1. Символу k соответствует значение начальной фазы, равное 2 k/M радиан, или 360k/M градусов.

В качестве примера построим график сигнала, содержащего все возможные символы при 4-позиционной ФМн. Его параметры:

M = 4; ( количество позиций манипуляции)

sy = 0:M-1; (передаваемые символы)

Fd = 1; (символьная скорость)

Fc = 4; (несущая частота)

FsFd = 40; % отношение Fs/Fd

Fs = Fd * FsFd; (частота дискретизации)

Формируем ФМн-сигнал:

[s_psk, t] = dmod(sy, Fc, Fd, Fs, 'psk', M);

plot(t, s_psk)

На графике сигнала, изображенного на рисунке 2, видны скачки фазы на 90° , происходящие при переходе от одного символа к другому.

Рисунок 2 Фазо-манипулированный сигнал

Для демодуляции фазоманипулированного сигнала используется команда

z = ddemod(S,Fc,Fd,Fs,'psk',M);

Необходимо учесть, что для правильного выполнения этой команды длина вектора S должна быть кратна величине Fs/Fd.

Аналогично формируется сигнал при частотной манипуляции. В качестве примера сформируем 2-позиционный (бинарный) ЧМн-сигнал, в котором возможным значениям символов 0 и 1 соответствуют частоты 800 и 1600 Гц. Символьная скорость будет равна 400 символам в секунду, а частота дискретизации — 16 кГц:

Пример 3. Обработка частотно- манипулированного сигнала

bits = [0 1 0 0 1]; (цифровое сообщение)

N = length(bits); (длина сообщения)

Fd = 400; (символьная скорость)

FsFd = 40; (отношение Fs/Fd)

Fs = Fd * FsFd; (частота дискретизации)

f0 = 800; (частота манипуляции для символа "0")

f1 = 1600; (частоты манипуляции для символа "1")

Fc = (f0 + f1)/2; (несущая частота)

tone = f1 – f0; (разнос частот)

td = t * Fd; ( время для графика – в символах)

Формируем ЧМн-сигнал Его вид представлен на рисунке 3.

[s_fsk, t] = dmod(bits, Fc, Fd, Fs, 'fsk', 2, tone);

plot(td, s_fsk)

xlabel('Symbols')

ylabel('s_{FSK}')

ylim([-1.1 1.1])

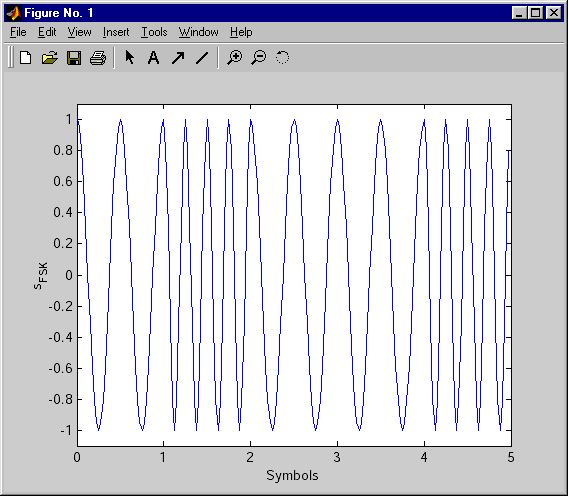
Рисунок 3 Частотно-манипулированный сигнал

На графике сигнала, изображенного на рисунке 3, хорошо заметно двукратное изменение частоты сигнала при смене значения передаваемого бита. В данном примере на длительности символа укладывается два периода колебания при передаче нулевого бита и четыре периода — при передаче единичного бита.

Демодуляция ЧМн-сигнала

Прием ЧМн-сигнала, как правило, осуществляется корреляционным методом. При этом корреляционный прием может быть когерентным или некогерентным. Когерентный метод может использоваться, если известны начальные фазы посылок. Если начальные фазы передаваемых посылок неизвестны (на практике так чаще всего и бывает), приходится использовать некогерентный (или квадратурный) корреляционный прием. В этом случае опорными сигналами служат не вещественные гармонические колебания, а комплексные экспоненты, а у результата интегрирования вычисляется модуль. Из-за игнорирования фазовой информации помехоустойчивость некогерентного метода несколько ниже, чем у когерентного.

Когерентный вариант демодуляции используется функциями ddemod и ddemodce по умолчанию. Для использования некогерентного варианта необходимо при вызове этих функций указать метод манипуляции в виде 'fsk/noncoherence'.

Указания по выполнению работы

Для выполнения частотной манипуляции/демодуляции заданного сигнала необходимо 1. квантовать исходный сигнал, чтобы размер алфавита М не превосходил М=30

2. не вводить параметр tone, тогда он по умолчанию будет равен Fd

3. повысить значения частот дискретизации входного Fs и выходного Fd сигналов

( например, Fd=100;Fs=60000).

4.построить графики демодулированных сигналов для когерентного и некогерентного приема и в выводах оценить влияние способа приема на сигнал.

Отчет должен содержать:

1. Задание на выполнение работы

2. Листинги моделирующих программ

3. Скрин-шоты результатов выполнения программ

4. Выводы

Контрольные вопросы:

1. Какой метод приема сигнала – когерентный или некогерентный – может обеспечить лучшее качество ( в смысле вероятности ошибки) и почему?

2. Как уменьшить вероятность ошибки при использовании более некачественного метода приема?