Министерство образования и науки Российской Федерации Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Российский государственный гидрометеорологический университет
Е.А.Чернецова
Теория передачи дискретных сообщений
Лабораторный практикум
Санкт-Петербург
2014
УДК 681.3.07
Чернецова Е.А. Теория передачи дискретных сообщений - СПб.: изд. РГГМУ, 2014.- с.
Рецензент И.В.Алешин, проф.Санкт-Петербургского государственного морского технического университета
Лабораторный практикум предназначен для студентов специальности «Информационная безопасность телекоммуникационных систем» . Используемые в тексте примеры программирования тестировались в пакете MATLAB.
Е.А. Чернецова 2007
Российский государственный гидрометеорологический университет (рггму), 2014 Лабораторная работа № 1 Изучение принципов аналоговой модуляции
Цель работы: изучение принципов аналоговой модуляции
Задание на выполнение работы:
Используя табличный процессор Excel, графически решить задачу, обратную задаче разложения в спектр периодического сигнала.
Осуществить моделирование аналоговой модуляции сигнала средствами пакета Matlab Communications Toolbox. Построить спектр сигнала до и после модуляции
Часть I
Используя
табличный процессор Excel,
графически решить задачу, обратную
задаче разложения в спектр периодического
сигнала. При этом считать, что периодический
сигнал состоит из четырех гармоник с
частотами
,
а амплитуды гармоник убывают и
соответственно равны 1/3, 1/5, 1/7 от амплитуды
основной гармоники
.
Уравнение гармонических колебаний в общем случае выражается формулой
, где
- текущее значение сигнала;
- амплитуда;
-
частота;
- начальная фаза сигнала
Исходные данные
Принять
,
где
- заданная цифра;
,
где
- текущая дата (день месяца);
=0
Порядок решения задачи
1. Подготовить таблицу по форме 1.1 ( рис.1.1)
Форма 1.1
2. Для записи параметров , , на свободном месте листа ( вне таблицы 1.1) выделить 3 ячейки1.
3. Заполнить графу 1. Для корректного графического отображения зависимостей таблица 1.1 должна содержать не менее 50 ячеек.
4.
Заполнить графу 2. В графе 2 время t
начинается
с нуля. Затем с шагом
определяются остальные значения. Шаг
сначала выбирается произвольно, а затем
изменяется таким образом, чтобы на
первом графике (см. рис.1.2) поместилось
не менее одного и не более двух периодов
основной гармоники
.
5. Графы 3,4,5,6 заполняются с учетом закона изменения амплитуд и частот гармоник в разложении Фурье. В этом случае уравнения примут вид:
и т.д.
6. Графа 7 получается сложением граф 3,4,5,6
7. Построить графики зависимостей для отдельных гармоник (см. рис.1.2)
8. Построить график итоговой зависимости ( по графе 7)
9. Подобрать значение начальной фазы сигнала таким образом, чтобы график изменения суммарного сигнала максимально приблизить к прямоугольной форме.
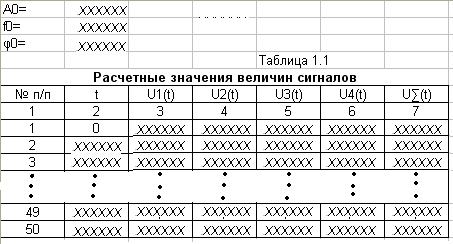
Рисунок 1.1 Образец выполнения таблицы 1.1
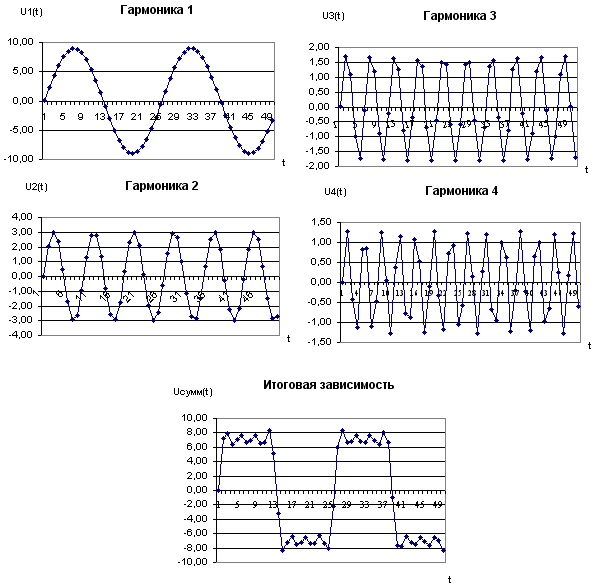
Рисунок 1.2 Формирование прямоугольного сигнала из гармоник