Лабораторная работа №7. Итерационные методы решения систем линейных уравнений. Приложения численных методов решения систем линейных уравнений Метод Зейделя

Метод Зейделя относится к итерационным методам решения систем линейных уравнений.

Подробное описание метода Зейделя можно посмотреть в книге Самарский А.А. «Введение в численные методы». Для каждого итерационного метода решение системы линейных уравнений находится в результате многократного повторения одной и той же вычислительной процедуры, которая называется итерационной. Каждое выполнение этой процедуры называется итерацией. В каждой итерации из начального значения вектора решений X в результате выполнения итерационной процедуры получается «новое» приближенное значение вектора решений Z. Если итерационный процесс сходится, то для каждой следующей итерации разность между векторами Х и Z постоянно уменьшается и после достаточно большого количества итераций может стать меньше заданной погрешности определения вектора решений.

Если система N линейных алгебраических уравнений записана в виде:

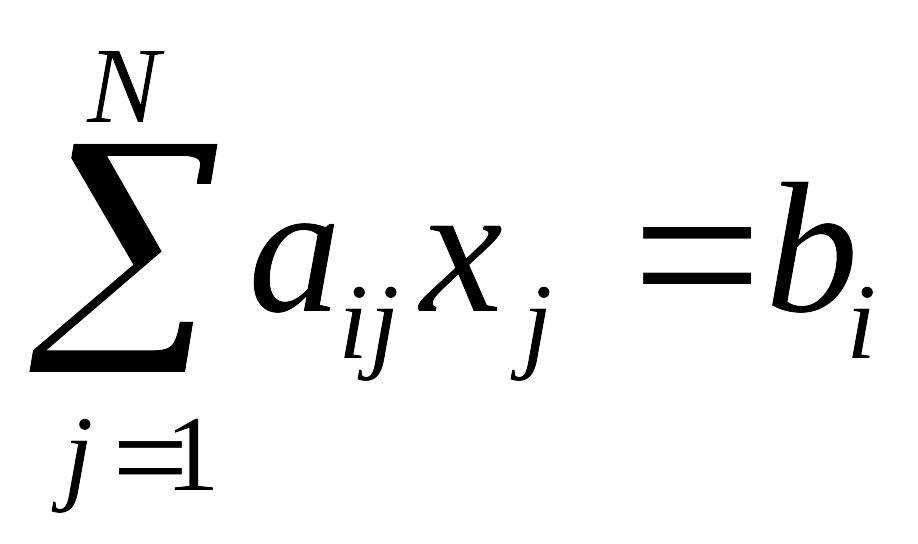, i=1, …, N (1)

где – вектора неизвестных и правых частей, – матрица коэффициентов.

Метод Зейделя применяется в одной из двух форм:

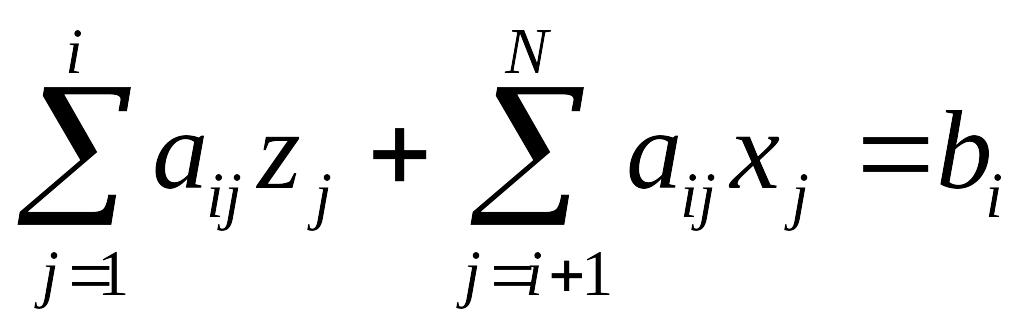, a_ij≠0, i=1, 2, …, N (2)

или

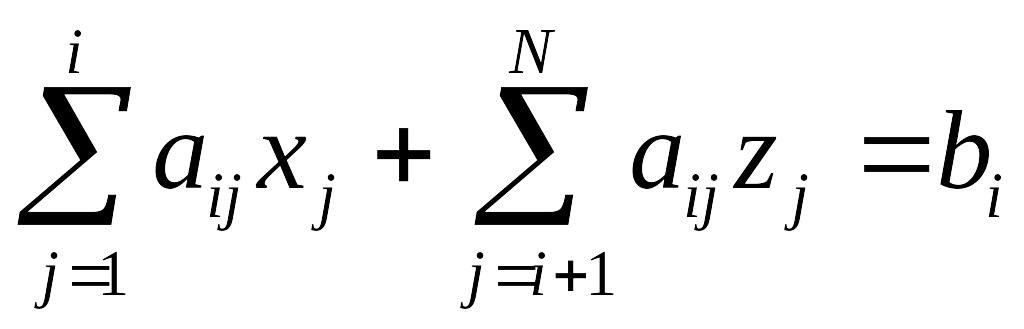, a_ij≠0, i=1, 2, …, N (3)

В расчетных формулах метода Зейделя (вариант (2), и (3)) Z – «новое» значение вектора неизвестных, а Х – начальное значение вектора Х для каждой итерации.

Рассмотрим вычислительную процедуру (2). Распишем формулу (2) для каждой строки i.

Для i=1:

,

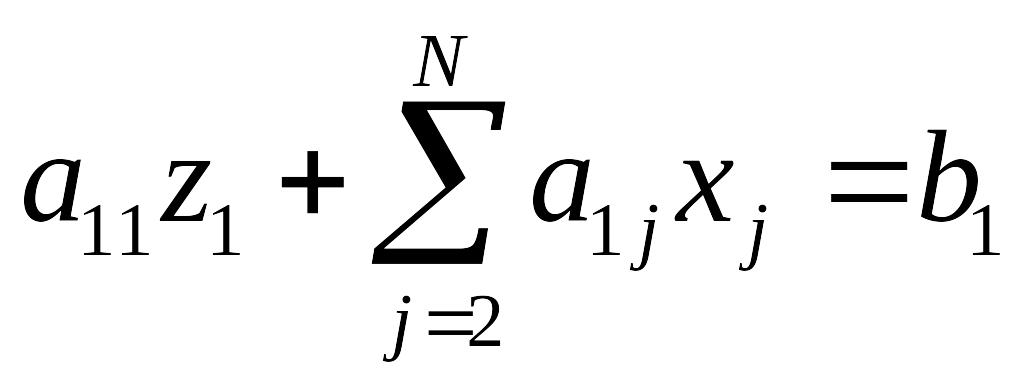Из этого уравнения легко находится первый элемент «нового» вектора решений z₁.

Для i=2

,

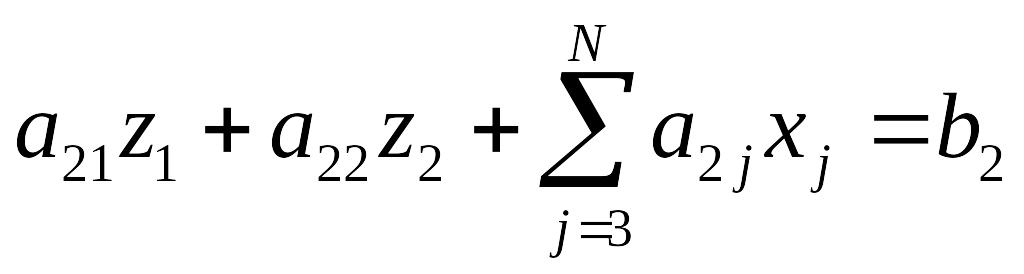из этого уравнения легко находится второй элемент «нового» вектора решений z₂,

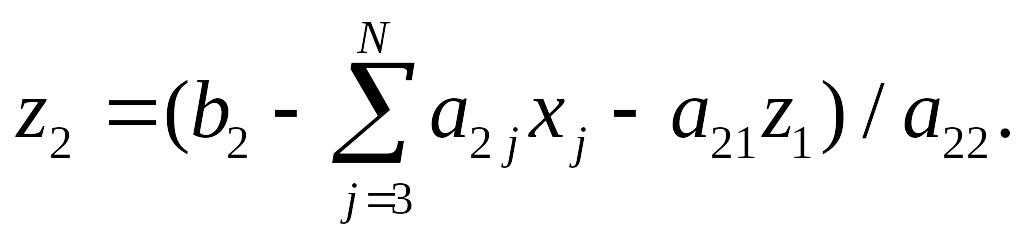
Для i=3

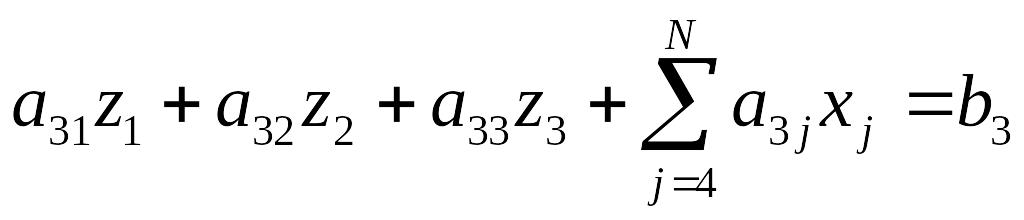, и т.д.

Для i=k

.

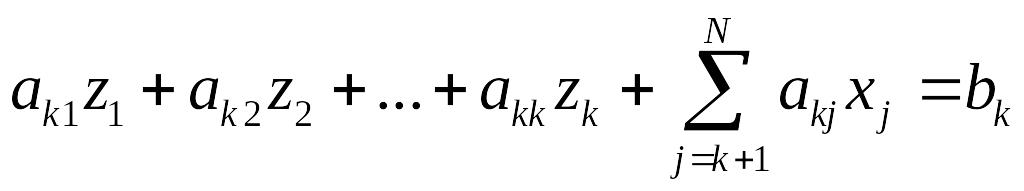Уравнение для строки с номером k можно записать в виде:

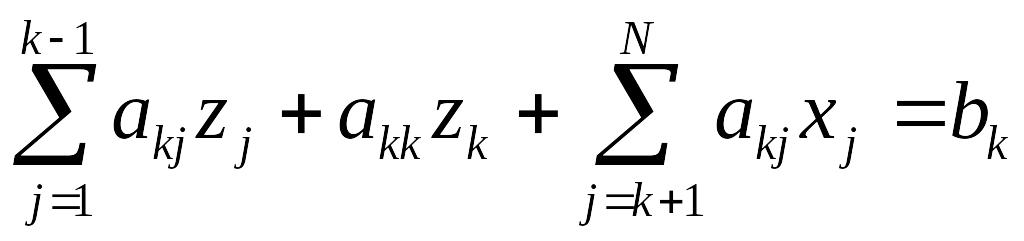, где k=1, …, N-1.

В этом уравнении первое слагаемое – 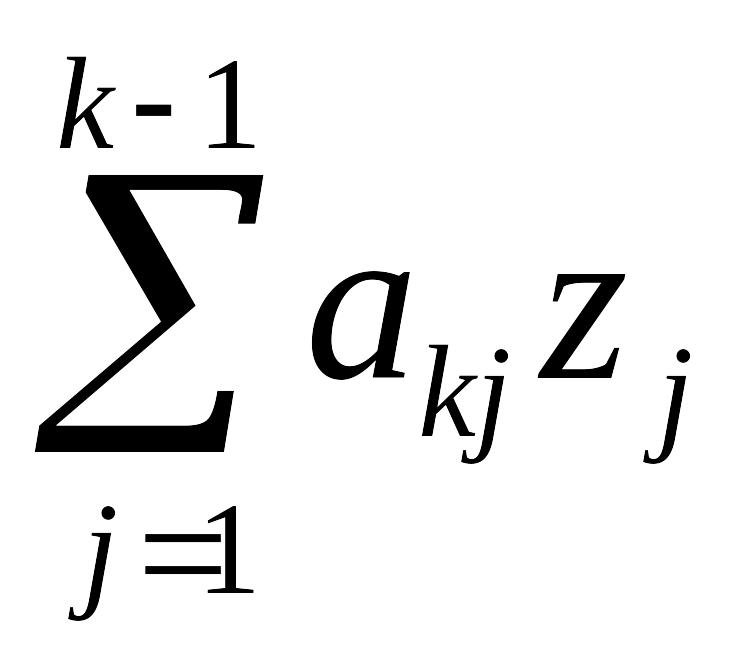состоит из известных величин матрицы коэффициентов и уже вычисленных элементов вектора решений z_j. Из него получаем значение k-й компоненты вектора решений – z_k.

Все компоненты «нового» вектора решений получаем в результате выполнения следующего алгоритма:

Цикл по k от 1 до N-1

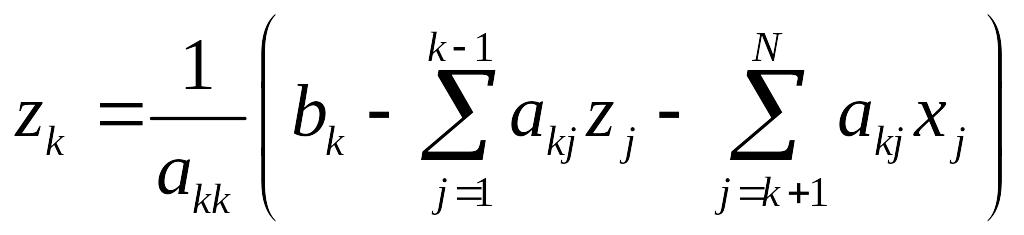
Конец Цикла

Распишем суммы в формуле в теле цикла. В результате получим более детализированный алгоритм:

Цикл по k от 1 до N

S1=0

Цикл по j от 1 до k-1

S1=S1+a_kj

Конец Цикла

S2=0

Цикл по j от k+1 до N

S2=S2+ a_kjx_j

Конец Цикла

=(b_k-S1-S2)/a_kk

Конец Цикла

Этот алгоритм представляет собой тело одной итерации. После получения «нового» значения вектора решений – Z, вычисляется разность векторов решений до и после итерации – d = |X-Z|. Если эта разность больше величины заданной допустимой погрешности – «новое» значение вектора решений присваивается начальному: X = Z и итерационный процесс продолжается. Начальные значение вектору X задают исходя из смысла задачи. Если d=|X-Z| меньше величины заданной допустимой погрешности – тогда итерационный процесс завершается.

Можно оптимизировать последний алгоритм, объединив циклы для вычислений S1 и S2. Поскольку в цикле для вычисления S1 компоненты получаются с предыдущей итерации, можно заменить на , подобную же замену можно произвести в выражении =(b_k-S1-S2)/a_kk в теле основного цикла.

Цикл по k от 1 до N

S=0

Цикл по j от 1 до N

Если j≠k

S=S+a_kjx_j

Конец Если

Конец Цикла

x_k=(b_k-S)/a_kk

Конец Цикла

Теперь можно записать полный алгоритм метода Зейделя с учетом определения максимального количества итераций, требуемой погрешности и т.д.

Алгоритм решения неоднородной системы линейных уравнений методом Зейделя на естественном языке:

n=КоличествоУравнений

ОпределитьМассив a(n,n), b(n), x0(n), x(n)

Max_i = МаксимальноеЗначениеИтераций

ERR=ЗначениеПогрешности

ПолучитьКоэффициенты(@а, @b, n)

ЗадатьНачальноеЗначение(@X)

Цикл по L от 1 до Max_i

Цикл по k от l до N

x0(k)=x(k)

Конец Цикла

Цикл по k от 1 до N

S=0

Цикл по j от 1 до N

Если j≠k

S=S+a(k,j)*x(j)

Конец Если

Конец Цикла

x(k)=(b(k)-S)/a(k,k)

Конец Цикла

DX=0

Цикл по k от 1 до N

DX = DX + (x(k)-Х0(k))^2

Конец Цикла

DX = КвадратныйКорень(DX)

Если DX < ERR Тогда

ПечатьРешения (@x)

ВыходИзЦикла

Иначе

Цикл по k от l до N

x0(k)=x(k)

Конец Цикла

Конец Если

Конец Цикла

Замечание. Матрица коэффициентов в методе Зейделя не должна иметь нулевые диагональные элементы, более того, для лучшей сходимости, можно преобразовать систему уравнений к виду, когда на главной диагонали находятся максимальные по модулю элементы соответствующих подматриц.

Пример реализации алгоритма решения неоднородной системы линейных уравнений методом Зейделя на VFP:

clear

local i, j, k, l, n

local lb, ub, DX

n = 3

max_i = 100

ErrX = 0.01

lb = -0.5

ub = 0.5

dec = 4

LOCAL ARRAY a(n,n), b(n), x(n), x0(n)

? "МАТРИЦА КОЕФИЦИЕНТОВ СИСТЕМЫ А(N,N)"

CreateRNDMartix(@a, n, lb, ub, dec, 1)

? "ВЕКТОР ПРАВОЙ ЧАСТИ СИСТЕМЫ B(N)"

CreateRNDVector(@b, n, lb, ub, dec, 1)

? "НАЧАЛЬНЫЕ ЗНАЧЕНИЯ ВЕКТОРА РЕШЕНИЙ X0(N)"

CreateRNDVector(@x0, n, lb, ub, dec, 1)

For l = 1 To max_i

For k = 1 To n

x(k) = x0(k)

ENDFOR

For k = 1 To n

s = 0

For j = 1 To n

If j <> k Then

s = s + a(k, j) * x(j)

EndIf

ENDFOR

x(k) = (b(k) - s) / a(k, k)

ENDFOR

DX = 0

For k = 1 To n

DX = DX + (x(k) - x0(k)) ^ 2

ENDFOR

DX = Sqrt(DX)

? " Итерация l = " + alltrim(STR(l)) + " : DX = " + TRANSFORM(DX,"99.99999999")

If DX < ErrX Then

?

? " РЕШЕНИЕ НАЙДЕНО "

Print_Vector(@x, n, dec)

EXIT For

Else

For k = 1 To n

x0(k) = x(k)

ENDFOR

ENDIF

ENDFOR

procedure CreateRNDMartix

LPARAMETERS a, n, lb, ub, dec, prnt

For i = 1 To n

For j = 1 To n

a(i, j) = (ub - lb) * Rand() + lb

a(i, j) = Round(a(i, j), dec)

ENDFOR

ENDFOR

If prnt = 1 Then

For i = 1 To n

?

For j = 1 To n

??(a(i, j))

ENDFOR

ENDFOR

ENDIF

ENDPROC

procedure CreateRNDVector

LPARAMETERS a, n, lb, ub, dec, prnt

For i = 1 To n

a(i) = (ub - lb) * Rand() + lb

a(i) = Round(a(i), dec)

ENDFOR

If prnt = 1 Then

For i = 1 To n

? a(i)

ENDFOR

ENDIF

ENDPROC

procedure Print_Vector

PARAMETERS x, n, dec

local DStr as String

DStr = "99."

For i = 1 To dec

DStr = DStr + "9"

ENDFOR

For i = 1 To n

? " X(" + ALLTRIM(STR(i)) + ") = " + TRANSFORM(x(i), DStr)

ENDFOR

ENDPROC

Пример реализации алгоритма решения неоднородной системы линейных уравнений методом Зейделя на VBA:

Sub Zeidel_test()

Dim i, j, k, l, n

Dim lb, ub, DX

Dim a(), b(), x(), x0()

n = 3

max_i = 100

ErrX = 0.01

lb = -0.5

ub = 0.5

dec = 4

ReDim a(n, n): ReDim b(n): ReDim x(n): ReDim x0(n)

Call CreateRNDMartix(a, n, lb, ub, dec, 1)

Call CreateRNDVector(b, n, lb, ub, dec, 1)

Call CreateRNDVector(x0, n, lb, ub, dec, 1)

For l = 1 To max_i

For k = 1 To n

x(k) = x0(k)

Next k

For k = 1 To n

s = 0

For j = 1 To n

If j <> k Then

s = s + a(k, j) * x(j)

End If

Next j

x(k) = (b(k) - s) / a(k, k)

Next k

DX = 0

For k = 1 To n

DX = DX + (x(k) - x0(k)) ^ 2

Next k

DX = Sqr(DX)

Debug.Print " Итерация l = " & l & " : DX = " & DX

If DX < ErrX Then

Debug.Print

Debug.Print " РЕШЕНИЕ НАЙДЕНО "

Call Print_Vector(x(), n, dec)

Exit For

Else

For k = 1 To n

x0(k) = x(k)

Next k

End If

Next l

End Sub

Sub CreateRNDMartix(a, n, lb, ub, dec, prnt)

Dim str

For i = 1 To n

For j = 1 To n

a(i, j) = (ub - lb) * Rnd() + lb

a(i, j) = Round(a(i, j), dec)

Next j

Next i

If prnt = 1 Then

str = ""

For i = 1 To n

For j = 1 To n

str = str & a(i, j) & " : "

Next j

str = str & vbCrLf

Next i

Debug.Print str

End If

End Sub

Sub CreateRNDVector(a, n, lb, ub, dec, prnt)

For i = 1 To n

a(i) = (ub - lb) * Rnd() + lb

a(i) = Round(a(i), dec)

Next i

If prnt = 1 Then

For i = 1 To n

Debug.Print a(i)

Next i

End If

End Sub

Sub Print_Vector(x(), n, dec)

Dim i

Dim DStr, str

DStr = "0."

For i = 1 To dec

DStr = DStr + "0"

Next i

str = ""

For i = 1 To n

str = str & "X(" & i & ") = " & Format(x(i), DStr) & vbCrLf

Next i

Debug.Print str

End Sub

Результат работы программ:

МАТРИЦА КОЕФИЦИЕНТОВ СИСТЕМЫ А(N,N)

0,4194 : 0,1317 : 0,1276 :

-0,0715 : -0,402 : 0,061 :

0,1945 : 0,4137 : 0,3348 :

ВЕКТОР ПРАВОЙ ЧАСТИ СИСТЕМЫ B(N)

-0,4774

0,0434

0,4162

НАЧАЛЬНЫЕ ЗНАЧЕНИЯ ВЕКТОРА РЕШЕНИЙ X0(N)

-0,0697

0,1779

0,0025

Итерация l = 1 : DX = 2,12836329279661

Итерация l = 2 : DX = 0,658840965997187

Итерация l = 3 : DX = 8,86987750634338E-02

Итерация l = 4 : DX = 1,74853648883518E-02

Итерация l = 5 : DX = 2,35213495124003E-03

РЕШЕНИЕ НАЙДЕНО

X(1) = -1,8062

X(2) = 0,4723

X(3) = 1,7088

Замечание: данные примеры реализаций алгоритмов используют системы уравнений, коэффициенты которых сформированы случайным образом, поэтому сходимость алгоритма зависит от «удачно сформированного» вектора начальных значений.