
- •Охарактеризуйте головны етапи процессу проектування доріг
- •Нназвіть головні передумови застосування засобів автоматизації для проектування доріг
- •3. Назвіть головні етапи впровадження автоматизованого проектування доріг
- •Назвіть головні задачі які вирішуються в системі сапад-ад
- •5. Назвіть головні передумови застосування засобів автоматизації робочих процесів дорожніх машин
- •6. Назвіть головні умови застосування засобів автоматизації робочих процесів дорожніх машин.
- •7. Які головні задачі вирішуються впров. Авт. Методів проектування доріг
- •8. Які головні задачі вирішуються впровадженням засобів автоматизації процесів роботи дбм
- •9. Назвіть головні передумови впровадження автоматизації в процес експлуатації доріг
- •10. Які головні задачі вирішуються впровадженням засобів авт..В процес експлуатації доріг
- •11. Назвіть відомі вам засоби автоматизованого проектування доріг
- •12. Охарактеризуйте відомі вам засоби автоматизованого проектування доріг
- •13. Поняття критерію проектування.Головні вимоги та методи вибору
- •14. Характеристика блоково-ієрархічного методу проектування
- •15. Охарактеризуйте основні методи пошуку оптимальних рішень
- •16. Охарактеризуйте відомі вам методи вибору кращого варіанту проектного рішення
- •17. Запишіть та поясніть задачу лінійного програмування в стандартній постановці Лінійне програмування
- •19. Запишіть та поясніть задачу не лінійного програмування в стандартній постановці
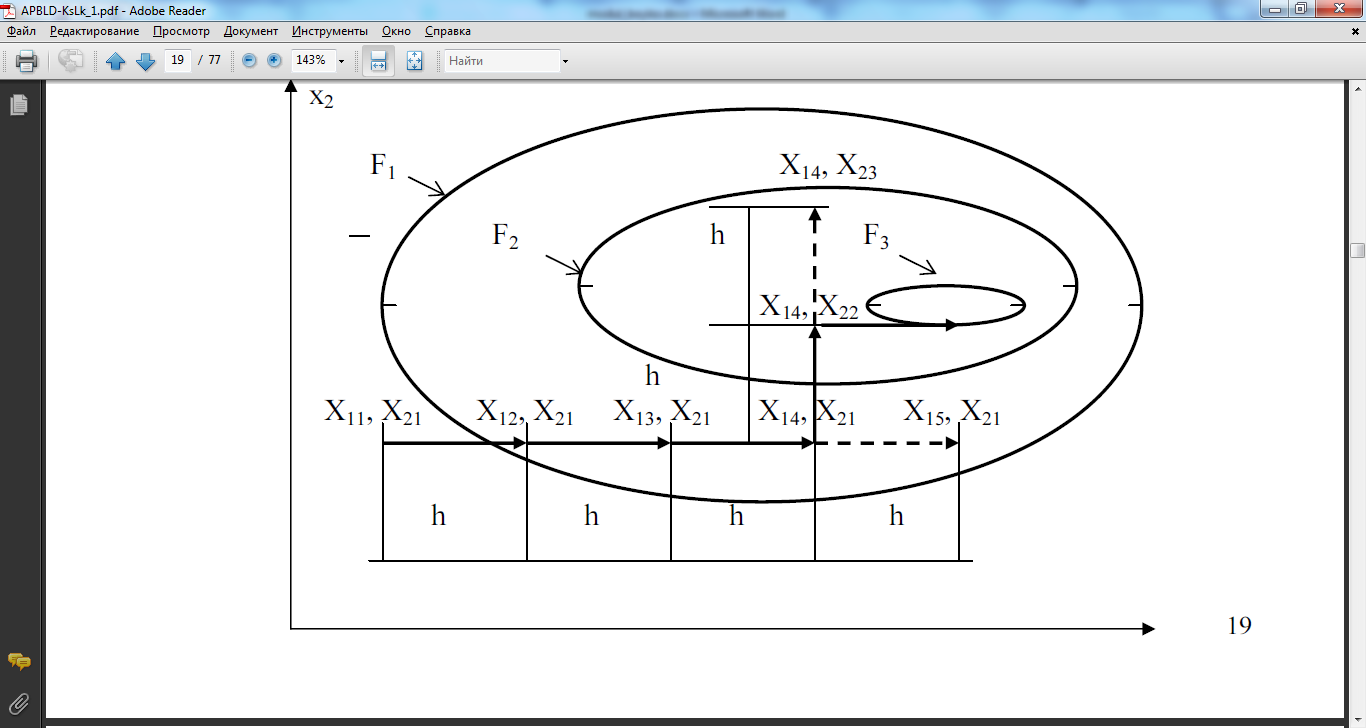
- •20. Поясніть суть методу по координатного спуску
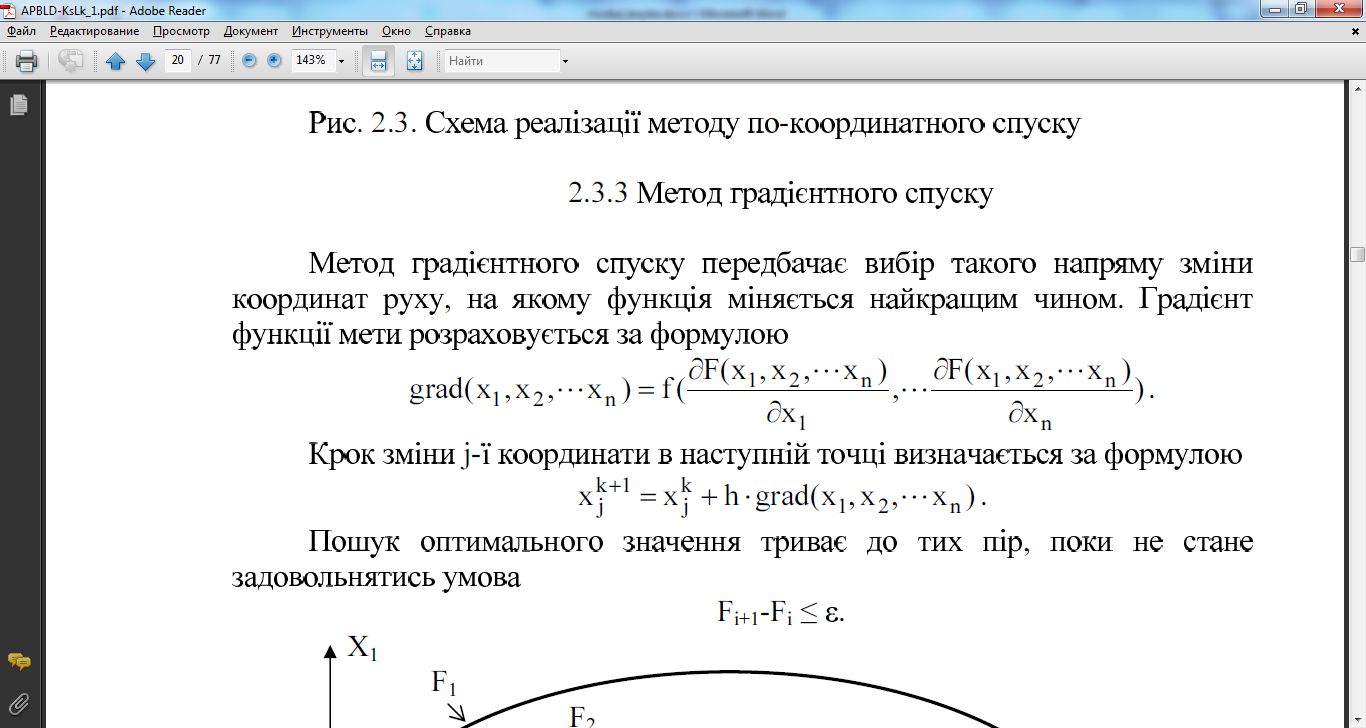
- •21. Поясність суть методу градієнтного спуску
- •22. Поясніть термін дорожній одяг
- •24. Які методи розрахунку нежорсткого до ви знаєте
- •25. Назвіть основні принципи конструювання до автомобільних доріг
- •26.Поясніть порядок розрахунку товщини покриття тришарового дорожнього одягу.
- •27. Поясніть порядок розрахунку товщини шару основи тришарового дорожнього одягу
- •28. Як розрахувати інтенсивність руху, якщо по дорозі рухаються різні транспортні засоби
- •29. Опишіть та поясніть основні рівняння граничного напруженого стану нежорсткого дорожнього одягу
- •30.Опишіть та поясніть головні рівняння граничного стану нежорсткого дорожнього одягу.
- •33,34 Поясніть основні положення розрахунку до за зсувними зусиллями. Як розрахувати допустиме зусилля зсуву у грунті
- •35,36 Як розрахувати покриття/проміжний шар на допустиме зусилля розтягу.
- •37. Поясніть головні положення розр до з умови морозного здимання
14. Характеристика блоково-ієрархічного методу проектування
Проектування
складних систем вимагає залучення до
роботи великої кількості спеціалістів
і значного періоду часу. Переваги
блокова-ієрархічного методу проектування
складних систем полягаюьб у тому,що
задача великої розмірності розбиваються
на задачі токої складності, що піддаються
осмисленню та розумінню проектувальника
і можуть бути розвязані
наявними технічними засобами і людськими
ресурсами.Розбивання складнох задачі
на рівні та блоки дозволяє доручити
рішення цих задач окремим
проектувальникам,підрозділами або
організаціям. 
15. Охарактеризуйте основні методи пошуку оптимальних рішень
Існує 4-ри методи:
1) Лінійне програмування




16. Охарактеризуйте відомі вам методи вибору кращого варіанту проектного рішення




17. Запишіть та поясніть задачу лінійного програмування в стандартній постановці Лінійне програмування
Стандартна постановка задачі на пошук оптимального рішення формулюється так:
Знайти екстремум функції мети
Р=СіХ!+ С2Х2+...СПХШ
на змінні якої накладені обмеження
апхі+аі2х2+... аіпхп<Ьі
а2іХі+ а22х2+ - • • а2пхп <^2 ат1Х1^ ат2х2^- • • атпхп<іт
за умов: хі>0 (І=1,п; ]=1,т; т>п)
де а, Ь, с - задані постійні величини.
Відомо кілька методів рішення задач лінійного програмування. Найпоширеніший сімплекс-метод, гнучкий і універсальний. Розроблене потужне математичне забезпечення, яке реалізує сімплекс-метод на ЕОМ.
Найкраще суть сімплекс-методу можна розглянути на прикладі рішення задачі пошуку екстремуму функції, яка залежить від 2-х параметрів.
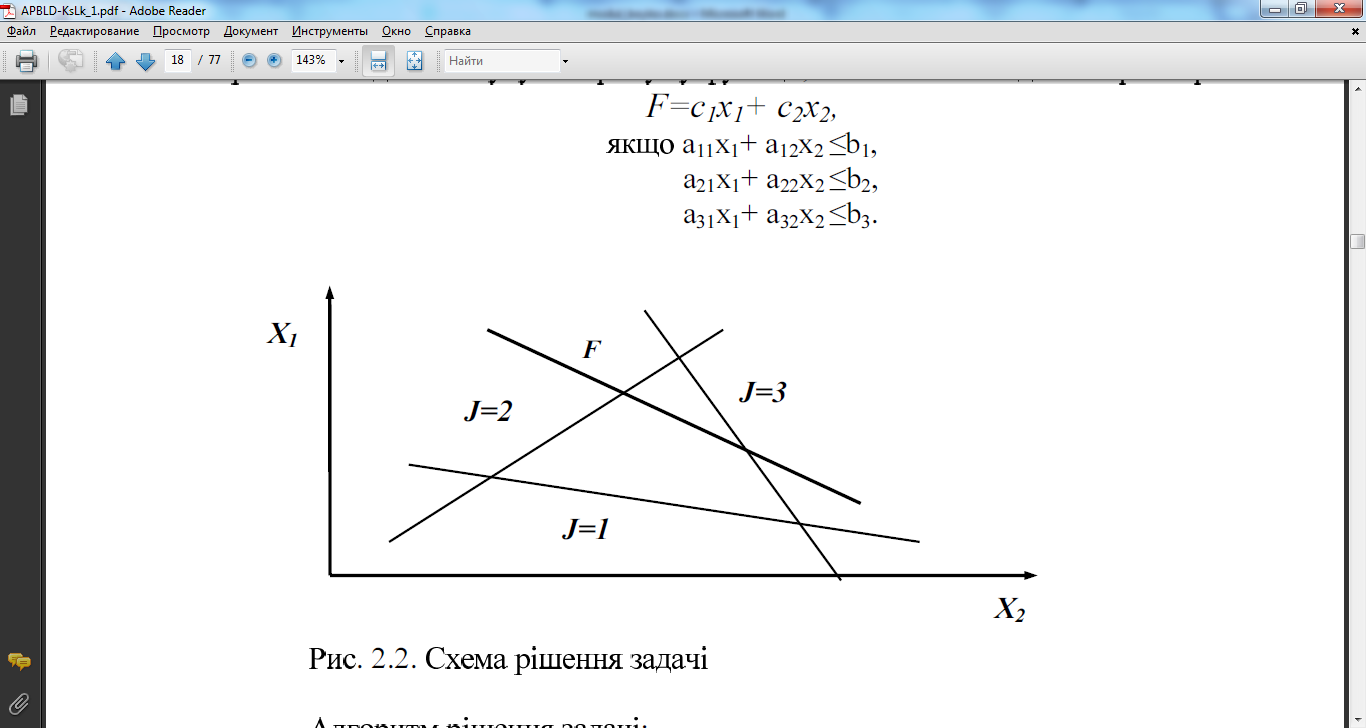
А=с1х1+ с2х2, якщо ацхі+ аі2х2<Ьь а2іхі+ а22х2 <Ь2, а3іхі+ а32х2<Ь3.
Рис.
2.2. С>сема рішення задачі Алгоритм
рішення задачі:
Знаждимо
координати (хь
х2)
однієї з вершин;
Знажщимо
значення функції в цій точці;
Знажщимо
значення функції в наступній точці;
Порівнюємо
одержані значення функції і вибираємо
краще;
Переходимо
на наступну вершину і перевіряємо
наступні два значення функції та
вибираємо краще
18.
Поясніть суть симплекс- методу рішення
задачілінійного програмування
Найпоширеніший сімплекс-метод, гнучкий і універсальний. Розроблене потужне математичне забезпечення, яке реалізує сімплекс-метод на ЕОМ.
Найкраще суть сімплекс-методу можна розглянути на прикладі рішення задачі пошуку екстремуму функції, яка залежить від 2-х параметрів.
А=с1х1+ с2х2, якщо ацхі+ аі2х2<Ьь а2іхі+ а22х2 <Ь2, а3іхі+ а32х2<Ь3.
Рис.
2.2. С>сема рішення задачі Алгоритм
рішення задачі:
Знаждимо
координати (хь
х2)
однієї з вершин;
Знажщимо
значення функції в цій точці;
Знажщимо
значення функції в наступній точці;
Порівнюємо
одержані значення функції і вибираємо
краще;
Переходимо
на наступну вершину і перевіряємо
наступні два значення функції та
вибираємо краще
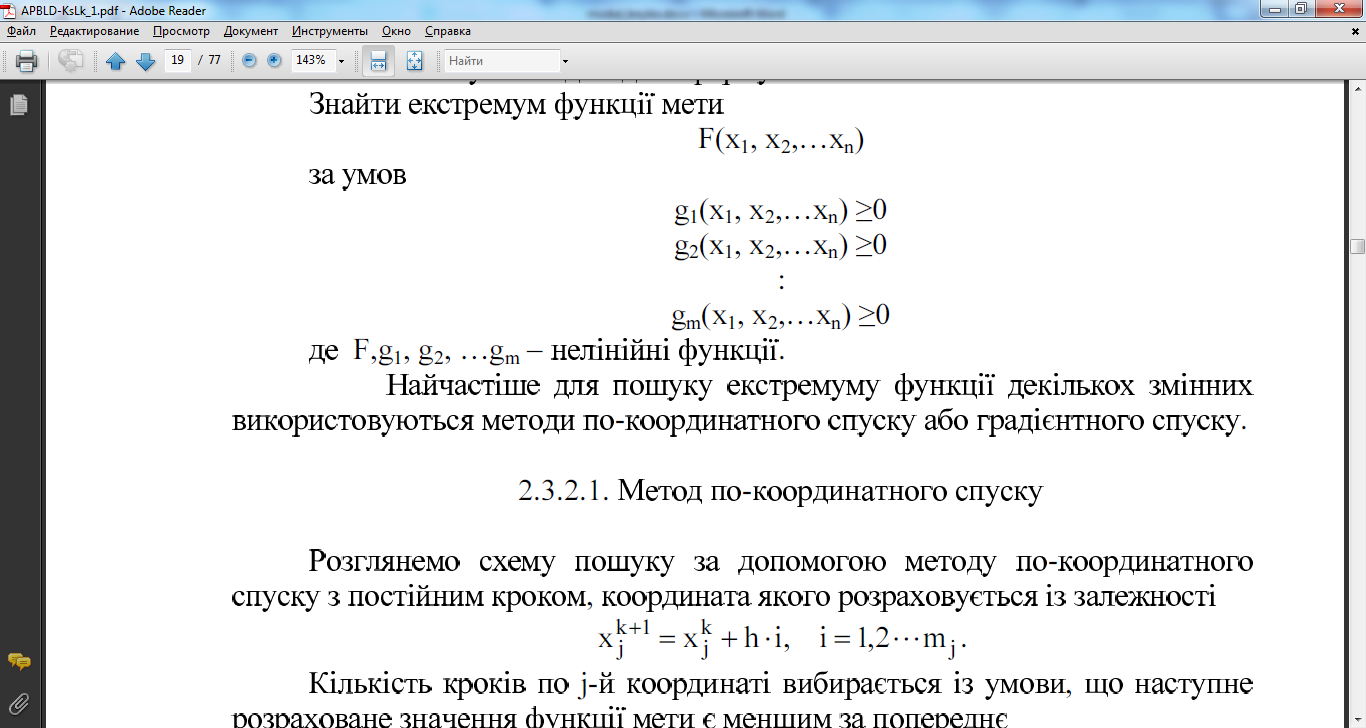
19. Запишіть та поясніть задачу не лінійного програмування в стандартній постановці
В загальному вигляді задача формулюється так:
Знайти екстремум функції мети
Р(хьх2,...хп)
за умов
§і(Хь Х2,^Хп)>0
§2(х1? Х2,^Хп)>0
^(хь х2,...хп) >0
де ¥&ь g2, .. .&п - нелінійні функції.
Найчастіше для пошуку екстремуму функції декількох змінних використовуються методи по-координатного спуску або градієнтного спуску
