6 Понятие об энергии Гиббса. Ее изменение в химических процессах.

Энергия Гиббса  (изобарно-изотермический потенциал). Во многих случаях самопроизвольные процессы (процессы, происходящие без подвода энергии от внешнего источника) в природе протекают при наличии разности потенциалов, например, разность электрических потенциалов, обусловливает перенос заряда, а разность гравитационных потенциалов – падение тела. Эти процессы заканчиваются при достижении минимума потенциала. Движущей силой  химических процессов, протекающих при постоянных давлении  и температуре является   изобарно-изотермический потенциал, называемый в настоящее время  энергией Гиббса и обозначаемый G. Изменение энергии Гиббса в химическом процессе определяется соотношением

                                       ΔG = ΔH –TΔS,                                 (2.16)

где ΔG – изменение энергии Гиббса химического процесса; ΔH – изменение энтальпии химического процесса; ΔS – изменение энтропии химического процесса; Т – температура в Кельвинах.

                Уравнение (2.16) может быть представлено в следующем виде: ΔH = ΔG + TΔS.  (2.17)

                 Смысл уравнения (2.17) в том, что часть теплового эффекта реакции расходуется на совершение работы (ΔG), а часть рассеивается в окружающую среду (TΔS). 

                Энергия Гиббса является критерием принципиальной возможности самопроизвольного протекания реакции. Если в ходе реакции энергия Гиббса уменьшается, то процесс может протекать в данных условиях самопроизвольно  ΔG < 0. Процесс в данных условиях неосуществим, если ΔG > 0.  Реакция является обратимой, т.е. может протекать и в прямом и в обратном направлении, если  ΔG = 0 (термодинамическое условие химического равновесия).

Эти соотношения применимы также к фазовым равновесиям, т.е. случаям, когда в равновесии находятся две фазы (агрегатных состояния) одного и того же вещества, например, лед и жидкая вода.

Энтальпийный и энтропийный факторы. Процессы  могут протекать самопроизвольно (ΔG<0), если они сопровождаются уменьшением энтальпии (ΔH<0) и увеличением энтропии системы (ΔS>0). Если же энтальпия системы увеличивается (ΔH>0), а энтропия уменьшается (ΔS<0), то такой процесс протекать не может (ΔG>0).  При иных знаках ΔS и ΔН принципиальная возможность протекания процесса определяется соотношением энтальпийного (ΔH) и энтропийного (ТΔS) факторов.

Если  ΔН>0 и ΔS>0, т.е. энтальпийная составляющая противодействует, а энтропийная благоприятствует протеканию процесса, то реакция может протекать самопроизвольно за счет энтропийной составляющей, при условии, что |ΔH|<|TΔS|.

Если, энтальпийная составляющая благоприятствует, а энтропийная противодействует протеканию процесса, то реакция может протекать самопроизвольно за счет энтальпийной составляющей, при условии, что |ΔH|>|TΔS|.

Влияние температуры на направление реакции.  Изменение знака энергии Гиббса произойдет при

                                                                        (2.21)

Очевидно, что смена знака энергии Гиббса с изменением температуры возможна только в  двух случаях: 1) ΔН>0 и ΔS>0 и 2) ΔН<0 и ΔS<0.  

Стандартная энергия Гиббса образования  -     это изменение энергии Гиббса реакции образования 1 моль соединения из простых веществ, устойчивых при стандартных условиях. Энергия Гиббса образования простых веществ принимается равной нулю. Стандартные энергии Гиббса образования веществ можно найти в соответствующих справочниках.

Энергия Гиббса химической реакции. Энергия Гиббса является функцией состояния, т.е. ее изменение в процессе не зависит от пути его протекания, а определяется исходным и конечным состоянием системы.  Следовательно, энергию Гиббса химической реакции (2.10) можно рассчитать по формуле

  

                Если условия отличаются от стандартных, то для нахождения   Δ_rG может быть использовано уравнение изотермы Вант-Гоффа, которое для реакции   (2.11)  между газами записывается  как

                   

а между растворенными веществами  -

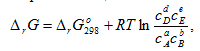                (2.24)

где    ^_ относительные  парциальные давления соответствующих веществ; с_А, с_В, с_D, c_E  ^_ концентрации соответствующих растворенных веществ, а, b, c, d – соответствующие стехиометрические коэффициенты.

                Если реагирующие вещества находятся в стандартном состоянии, то уравнения (2.23) и (2.24) превращаются в