13 Квантово-механическая модель строения атома. Квантовые числа и их физический смысл. Атомные орбитали.

В основу КММ положена квантовая теория атома, согласно которой электрон обладает как свойствами частицы, так и свойствами волны. Другими словами, о местоположении электрона в определенной точке можно судить не точно, а с определенной долей вероятности. Поэтому в КММ орбиты Бора заменили орбиталями (эдакие "электронные облака" - области пространства в которых существует вероятность пребывания электрона).  Квантовые числа и их физический смысл

      Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел. "Задайте значения квантовых чисел, и я полностью опишу свойства атома" - так может современный физик перефразировать известное изречение Архимеда.

      Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.

      1. Главное квантовое число  . Это квантовое число принимает значения

     

     и определяет полную энергию электрона в любом квантовом состоянии

.

(5.37)

      Можно отметить, что эти значения энергии являются собственными значениями гамильтониана (5.17a). Поэтому в связанном состоянии электрон в атоме водорода имеет дискретный энергетический спектр, лежащий в области отрицательных значений и имеющий точку сгущения  .

      2. Орбитальное (азимутальное) квантовое число  . В квантовых состояниях с заданным значением главного квантового числа   азимутальное квантовое число может иметь следующие значения:

.

  Из выводов предыдущего параграфа следует, что стационарные волновые функции  , описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии  , но и оператора квадрата момента импульса  , причем     

.

      Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:

.

(5.38)

      Проанализируем эту формулу квантования момента импульса. Сравнивая ее с условием (5.3) квантования момента импульса движущегося электрона в теории Бора, можно заметить, что эти условия не совпадают. И дело не только в отличии числовых значений, рассчитанных по этим формулам. Принципиальное отличие этих соотношений состоит в том, что в квантовой механике возможны состояния атома с нулевым моментом импульса. Во всех  -состояниях и, частности, в основном  -состоянии, когда  , по формуле (5.38) получаем  .

      При классическом описании движения электрона в атоме по определенной траектории (орбите) в любом состоянии атом должен обладать ненулевым моментом импульса.

      Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами. Следовательно, опыт подтверждает, что только отказ от классического траекторного способа описания движения электрона в атоме позволяет правильно рассчитать и предсказать свойства атома. Вероятностный способ описания движения частиц в квантовой механике является единственно правильным способом описания свойств атомных систем - таков вывод современной физики.

      Так как движущийся вокруг ядра электрон является заряженной частицей, то такое движение обуславливает протекание некоторого замкнутого тока в атоме, который можно охарактеризоватьорбитальным магнитным моментом .

      В теории Бора, когда с позиции классической теории рассматривается круговое движение электрона по орбите радиуса   со скоростью  , величина орбитального механического момента равна  . Если время полного оборота электрона  , то такому движению соответствует замкнутый ток

,

     который можно охарактеризовать величиной магнитного момента

.

     Связь механического и магнитного моментов при этом определяется гиромагнитным отношением

.

(5.39)

     Так как заряд электрона отрицателен, то для орбитального движения направление вектора магнитного момента   противоположно направлению вектора механического момента импульса  (рис. 5.8).

      Для расчета орбитального магнитного момента в квантовой теории следует определить пространственную плотность электрического тока   через плотность потока вероятностей   по формуле:  . Плотность потока вероятности при этом можно найти по формуле (3.23), зная волновую функцию электрона в заданном квантовом состоянии атома. Точный квантовомеханический расчет гиромагнитного отношения также приводит к формуле (5.39).

      Итак, в любом квантовом состоянии атом водорода обладает не только механическим моментом  , величина которого определяется формулой (5.38), но и магнитным моментом.

.

(5.40)

      Здесь универсальная постоянная

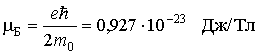
     служит единицей измерения магнитных моментов атомов и называется магнетоном Бора.

      Если атом переходит из одного квантового состояния в другое с испусканием (поглощением) фотона излучения, то возможны лишь такие переходы, для которых орбитальное квантовое число  изменяется на единицу. Это правило, согласно которому для оптических переходов  , называется правилом отбора. Наличие такого правила отбора обусловлено тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для электрона всегда на единицу.

      3. Магнитное квантовое число  . В квантовом состоянии с заданным значением орбитального квантового числа  , магнитное квантовое число может принимать   различных значений из ряда

.

      Физический смысл магнитного квантового числа вытекает из того, что волновая функция  , описывающая квантовое состояние электрона в атоме водорода, является собственной функцией оператора проекции момента импульса  , причем   

.

      Поэтому, из общих положений квантовой механики (см. раздел 3.5) следует, что проекция момента импульса электрона на выделенное в пространстве направление   может иметь только определенные значения, равные

.

(5.41)

      Направление   в пространстве обычно выделяется внешним полем (например, магнитным или электрическим), в котором находится атом.

      Так как формула (5.41) квантования проекции механического момента соответствует вполне определенным направлениям ориентации в пространстве вектора   (рис. 5.9), то эту формулу называют обычно формулой пространственного квантования.

      С точки зрения классического представления об электронной орбите, с учетом перпендикулярности вектора   к плоскости орбиты, соотношение (5.41) определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.

Отмеченная выше связь механического и магнитного моментов атома позволяет с учетом (5.41) записать также возможные значения проекции магнитного момента атома на выделенное направление  :

,

(5.42)

     зависящие от значения магнитного квантового числа  .

Атомная орбиталь — одноэлектронная волновая функция, полученная решением уравнения Шрёдингера для данного атома[1], задаётся главным n, орбитальным l и магнитным m квантовыми числами.

Волновая функция рассчитывается по волновому уравнению Шрёдингера в рамках одноэлектронного приближения (метод Хартри — Фока) как волновая функция электрона, находящегося в самосогласованном поле, создаваемым ядром атома со всеми остальными электронами атома.

Сам Э.Шрёдингер рассматривал электрон в атоме как отрицательно заряженное облако, плотность которого пропорциональна квадрату значения волновой функции в соответствующей точке атома. В таком виде понятие электронного облака было воспринято и в теоретической химии.

Однако большинство физиков не разделяли убеждений Э.Шрёдингера — доказательства существования электрона как «отрицательно заряженного облака» не было. Макс Борн обосновал вероятностную трактовку квадрата волновой функции. В 1950 г. Э.Шрёдингер в статье «Что такое элементарная частица?» вынужден согласиться с доводами М.Борна, которому в 1954 году присуждена Нобелевская премия по физике с формулировкой «За фундаментальное исследование в области квантовой механики, особенно за статистическую интерпретацию волновой функции».

Название «орбиталь» (а не орбита) отражает геометрическое представление о стационарных состояниях электрона в атоме; такое особое название отражает тот факт, что состояния электрона в атоме описывается законами квантовой механики и отличается от классического движения по траектории. Совокупность атомных орбиталей с одинаковым значением главного квантового числа n составляют одну электронную оболочку.
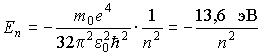