суть метода наименших квадратов

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным

. Суть метода наименьших квадратов (мнк).

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b   принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

13 Расчет вектора оценок коэффициентов регрессии

Для расчета вектора оценок коэффициентов регрессии   по методу наименьших квадратов используется формула , (2.4) где 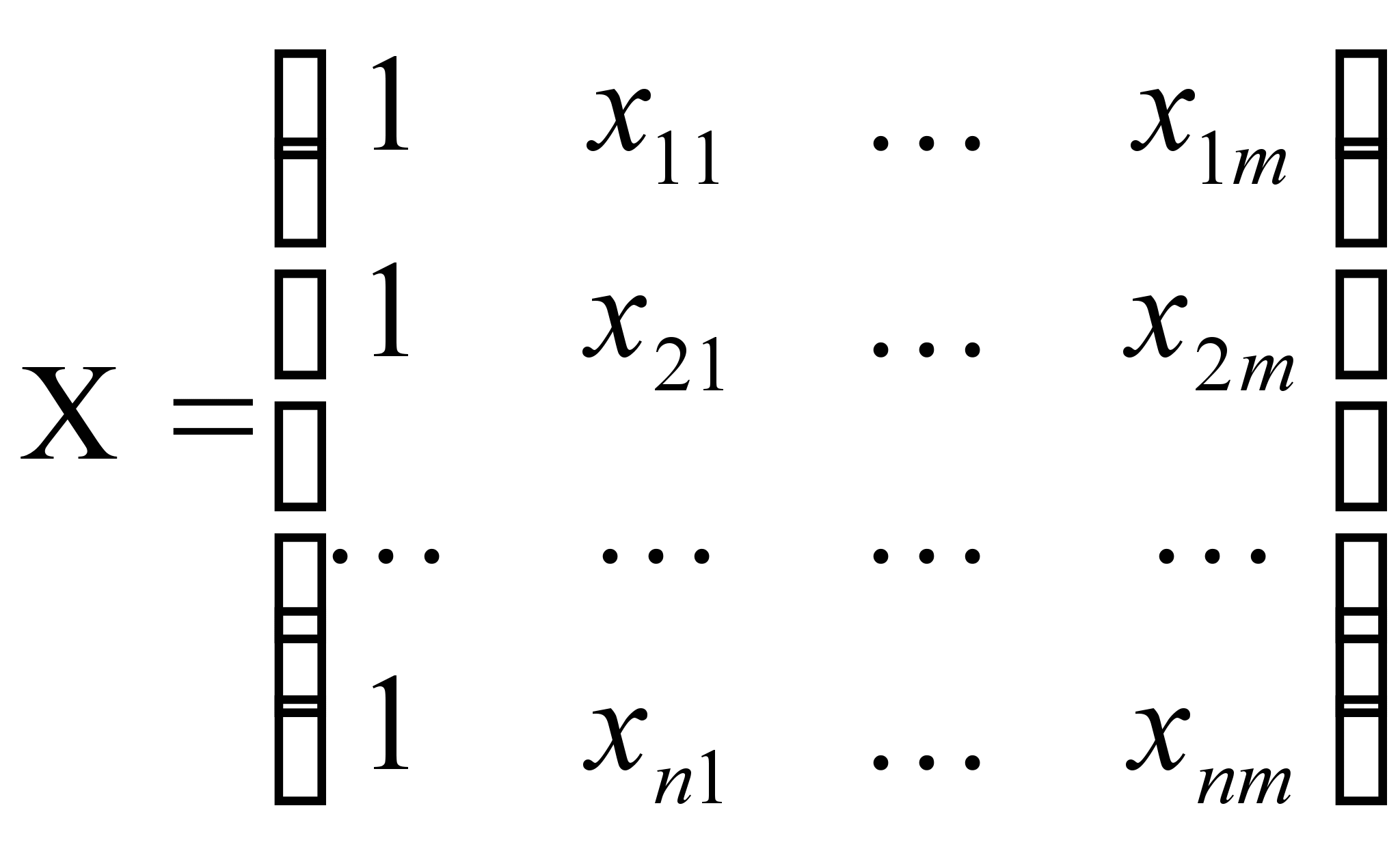 ;  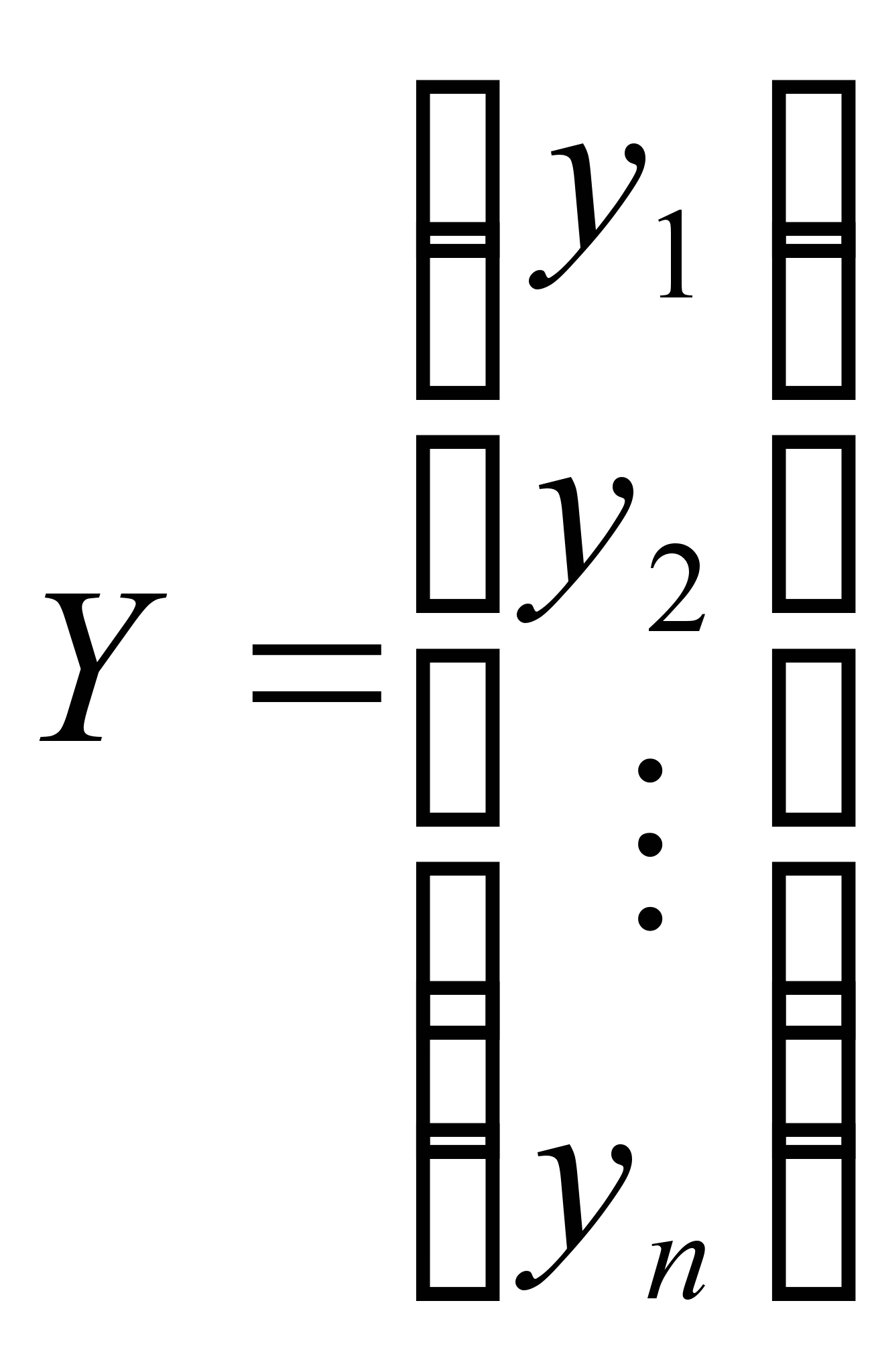;  ;     где  – транспонированная матрица X;   – матрица, обратная матрице  .

15Нулевая гипотеза – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Примером нулевой гипотезы в педагогике является утверждение о том, что различие в результатах выполнения двумя группами учащихся одной и той же контрольной работы вызвано лишь случайными причинами.

Выдвинутая гипотеза может быть правильной или неправильной, поэ­тому возникает необходимость проверить ее. Так как проверку произво­дят статистическими методами, то данная проверка называется статистической.

При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов:

—   можно отвергнуть нулевую гипотезу, когда она на самом деле верна (так называемая ошибка первого рода);

—   можно принять нулевую гипотезу, когда она на самом деле не верна (так называемая ошибка второго рода).

16Какой тест при проверке значимости

t-статистика соизмеряет значение коэффициента с его стандартной ошибкой. Фактически же мы проверяем гипотезу о том, равен нулю коэффициент при рассматриваемой переменной или нет. Т.е:

Ho: коэффициент=0. Если эта гипотеза верна, то коэффициент не значим.

Ha: коэффициент не равен 0. Если эта гипотеза верна, то коэффициент значим.

17 Стандартная ошибка коэффициента регрессии

20 Характеристики для проверки адекватности

Адекватность модели  — совпадение свойств (функций/параметров/характеристик и т.п.) модели и соответствующих свойств моделируемого объекта. Адекватностью называется совпадение модели моделируемой системы в отношении цели моделирования.

Адекватность ощущения и восприятия (от лат. adaequatus — приравненный, равный) — инвариантность основных свойств субъективного образа, его соответствие конвенциональному описанию объекта. Неадекватный образ отражения, как, например, в иллюзиях восприятия, рассогласован с другими формами перцептивного и когнитивного опыта индивида.

Оценка адекватности модели  - проверка соответствия модели реальной системе. Оценка адекватности модели реальному объекту оценивается по близости результатов расчетов экспериментальным данным.

Два основных подхода к оценке адекватности:

1) по средним значениям откликов модели и системы

Проверяется гипотеза о близости средних значений каждой n-й компоненты откликов модели Yn известным средним значениям n-й компоненты откликов реальной систем.

2) по дисперсиям отклонений откликов модели от среднего значения откликов систем

Сравнение дисперсии проводят с помощью критерия F (проверяют гипотезы о согласованности), с помощью критерия согласия ?2 (при больших выборках, п>100), критерия Колмогорова- Смирнова (при малых выборках, известны средняя и дисперсия совокупности), Кохрена и др.

22Какой тест при проверке адекватности

1. F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы H0 остатистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт  и критического (табличного) Fтабл значений F-критерия Фишера. Fфактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где   n – число единиц совокупности;

        m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a  –  вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если  Fтабл< Fфакт, то H0  – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если  Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначим

25Свойства коэффициентов регрессии

• коэффициенты регрессии имеют одинаковый знак , совпадающий со знаком м;

• коэффициенты регрессии являются угловыми коэффициентами для соответствующих прямых I и II относительно соответствующих осей, поэтому, если м > 0 и коэффициент регрессии отрицателен, то обе прямые наклонены налево.

• Замечание: Прямые регрессии пересекаются в точке А с координатами .

• Связь между коэффициентами корреляции и коэффициентами регрессии.

• Сравнивая формулы 11, 12 и 13 получаем, что

• ,

• где значение r выбирается так, чтобы он совпадал со знаком м.

ость, надежность уравнения регрессии.