Глава 2. Кинематика точки

2.1. Способы задания движения точки

Решение основной задачи кинематики зависит от способа задания движения точки. Есть три способа задания движения: векторный, координатный и естественный. Первый из них в основном представляет теоретический интерес, а два других применяют на практике.

Векторный способ задания движения. Положение движущейся точки в пространстве в каждый момент времени определяется заданием ее радиус-вектора r, эта зависимость

r = r (t) (2.1)

и представляет собой закон движения в векторной форме.

Кривая, которую описывает конец радиус-вектора r при изменении времени t от нуля до бесконечности и которая называется годографом этого вектора, будет траекторией точки.

Координатный способ задания движения. Положение точки в пространстве можно однозначно определить заданием ее координат, например, в прямоугольной декартовой системе отсчета. При этом уравнения движения точки:

x = f₁ (t);

y = f₂ (t); (2.2)

z = f₃ (t),

будут представлять собой не только закон движения, но и уравнение траектории в параметрической форме.

Мы ограничимся рассмотрением уравнений движения в прямоугольной декартовой системе координат, хотя на практике широко применяют и другие системы отсчета. Например – полярные, сферические или цилиндрические координаты.

Естественный способ задания движения. Этот способ задания движения требует знания:

– траектории точки;

– начала и положительного направления отсчета дуговой координаты;

– закона изменения дуговой координаты s = s(t).

При этом за начало отсчета удобно выбрать начальное положение точки, а положительное направление отсчета – совпадающим с направлением скорости в начальный момент времени.

2.2. Скорость и ускорение при векторном способе задания движения

Пусть известна зависимость (2.1) и нужно найти скорость и ускорение точки.

Скорость точки. Рассмотрим движущуюся точку на отрезке траектории, и пусть в моменты времени t и t + Δt она занимает положения М и М´ (рис. 2.1).

Вектор ММ´= Δr = r(t + Δt) – r(t) называется вектором перемещения точки за время Δt.

Вектор v_ср = Δr/Δt называется вектором средней скорости точки за этот промежуток времени, он направлен по хорде ММ´.

Вектор скорости в момент времени t определяется как предел этого отношения при стремлении промежутка времени к нулю: v(t) = Δr/Δt = dr/dt .

Отметим, что М´→ М при Δt → 0 , а предельное положение секущей ММ´ определяет касательную к кривой в точке М, поэтому можно дать следующее определение скорости точки.

Вектор скорости точки v равен производной от радиус-вектора r по времени и направлен по касательной к траектории в сторону движения:

v(t) = dr/dt. (2.3)

Ускорение точки. Рассмотрим точку на траектории в моменты времени t и t + Δt (рис.2.2, а). Пусть точке М соответствует скорость v(t), а точке М´ скорость v(t + Δt).

Вектор Δv = v(t + Δt) – v(t) называется вектором изменения скорости точки за время Δt.

Вектор a_ср = Δv/Δt называется вектором среднего ускорения точки за этот промежуток времени, он направлен по вектору Δv и лежит в плоскости, через которую проходят векторы v(t) и v(t + Δt), если последний вектор также перенести в точку М.

Вектор ускорения в момент времени t определяется как предел этого отношения при стремлении промежутка времени к нулю: a(t) = Δv/Δt = dv/dt.

Чтобы определить направление этого вектора построим годограф вектора скорости (рис. 2.2, б), на котором точкам М и М´ будут соответствовать точки N и N´, и проведем через точку М´ плоскость, в которой лежит вектор v(t). Предельное положение этой плоскости при М´ → М определяет соприкасающуюся плоскость в точке М. Теперь можно полностью определить ускорение точки.

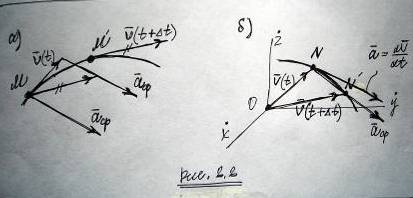
Вектор ускорения точки a равен производной от вектора скорости v по времени, лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории.

a(t) =dv/dt = d²r/dt². (2.4)