5.6. Частные случаи определения положения мцс

В предыдущем параграфе мы выяснили, как найти скорости точек плоской фигуры, если известно положение мгновенного центра скоростей.

Сейчас мы рассмотрим обратную задачу: как по информации о скоростях точек плоской фигуры определить положение ее МЦС.

1. Пусть известны направления скоростей двух точек А и В плоской фигуры, которые непараллельны друг другу (рис.5.9).

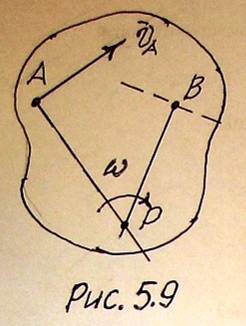
В каждый момент времени плоское движение тела можно заменить его вращательным движением относительно МЦС. А поскольку скорости точек вращающегося тела перпендикулярны отрезкам, соединяющим эти точки с центром вращения, то МЦС Р плоской фигуры будет находиться в точке пересечения перпендикуляров к скоростям v_А и v_В.

2. Пусть известны векторы скоростей двух точек А и В плоской фигуры, которые параллельны друг другу: v_A || v_B. Рассмотрим варианты, возможные в этом случае.

а). v_A ↑↑ v_B , v_A ^АВ , v_A ≠ v_B . Поскольку скорости точек вращающегося тела пропорциональны расстояниям от оси вращения, центр Р будет находиться на пересечении двух прямых: одна проходит через концы векторов v_A и v_B, а другая – через точки А и В (рис. 5. 10, а).

б). v_A ↑↓ v_B , v_A ^ АВ , v_A ≠ v_B . Этот случай принципиально не отличается от предыдущего (рис. 5. 10, б).

в). v_A ↑↑ v_B , v_A ^ АВ , v_A = v_B . За исходный возьмем случай а), зафиксируем v_A, а величину v_B устремим к v_A. Тогда точка пересечения прямых, в которой находится МЦС Р устремится в бесконечность, то есть в этом случае АР = ∞, а ω = v_A /АР = 0. Это означает, что в данный момент времени плоская фигура движется поступательно (рис. 5.10, в).

г). v_A || v_B , но v_A не перпендикулярна АВ. По теореме о проекциях скоростей точек плоской фигуры v_A = v_B. Как и в случае в) это означает, что в данный момент времени тело движется поступательно, то есть АР = ∞, а ω = v_A /АР = 0 (рис. 5.10, г).

При таком мгновенно поступательном движении скорости всех точек тела равны, но ускорения различны – в отличие от чисто поступательного движения тела .

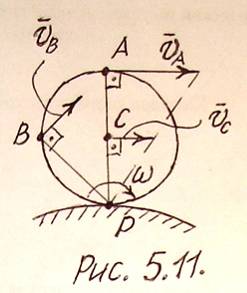
3. Пусть колесо движется без проскальзывания по неподвижной поверхности. Точка контакта неподвижна, поэтому по определению является мгновенным центром скоростей колеса (рис.5.11).

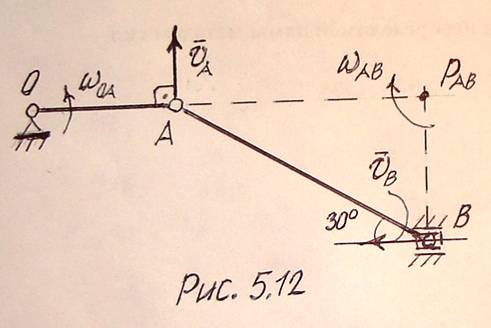
Пример 5.2. Определить скорость ползуна В в указанном положении кривошипно-шатунного механизма, если кривошип ОА длиной 1 м вращается со скоростью с^–1 (рис.5.12).

5.7. Теорема об ускорениях точек плоской фигуры

Теорема. Ускорение любой точки В плоской фигуры равно геометрической сумме ускорения полюса А и ускорения точки В в ее вращении вокруг полюса А.

Доказательство. По теореме о скоростях точек плоской фигуры (§5.2)

v_B = v_A + v_AB ω  AB. (5.1´)

Дифференцируя по времени, получим:

dv_B /dt = dv_A /dt + (dω/dt)AB + ω(dAB/dt),

или

a_B = a_A + a^ε_AВ + a^ω_AВ = a_A + a_AВ, (5.3)

где a^ε_AВ = ε  AB и a^ω_AВ = ω  v_AB соответственно вращательное и центростремительное ускорение точки В в ее вращении относительно полюса А (рис.5.13).

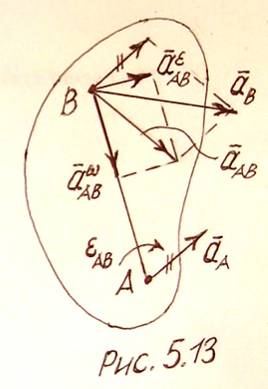
Модули этих ускорений равны:

| a^ε_AВ | = a^ε_AВ = ε · AB, (5.4)

| a^ω_AВ | = a^ω_AВ = ω² · AB. (5.5)

Теорема доказана.

Примечания

1. Отметим сходство в подходе к решению задач по кинематике на тему плоское движение и задач по статике на тему плоская система сходящихся сил.

В статике мы исходили из условия равновесия:

ΣF_i = 0, (а)

которое интерпретировали графически – как замкнутость силового многоугольника, или аналитически – как уравнения равновесия:

ΣX_i = 0, ΣY_i = 0. (б)

При графическом решении в качестве неизвестных выступали модуль и направление неизвестной реакции или модули двух известных по направлению реакций. При аналитическом решении – это были проекции двух неизвестных реакций на оси координат.

В кинематике вместо (а) выступают другие векторные равенства – (5.1) или (5.3):

v_B = v_A + v_AB (5.1´)

и

a_B = a_A + a^ε_AВ + a^ω_AВ (5.3´)

соответственно. Эти векторные уравнения, как и (а) содержат не более двух неизвестных, в качестве которых выступают модули и направления неизвестных скоростей и ускорений точек тела или его угловые скорости и ускорения.

Решение, как и в статике можно найти графически или аналитически из уравнений, аналогичных (б), которые получаются проектированием (5.1´) и (5.3´) на оси координат.

2. При графическом решении мы сразу определяем истинное направление реакции связи – в (а), или скорости и ускорения – в (5.1´) и (5.3´).

При этом векторные многоугольники для (5.1´) и (5.3´) в отличие от силовых многоугольников в статике являются незамкнутыми, поскольку соответствуют рассмотрению не уравновешенной системы сил, а нахождению равнодействующей системы сходящихся сил, равной сумме векторов.

3. При аналитическом решении результат может получиться отрицательным – это означает, что мы не угадали истинное направление реакции связи или кинематического параметра движения.

Если найденное неизвестное будет использоваться в дальнейшем решении, рекомендуется изменить его направление на противоположное и решить задачу заново, чтобы результат получился положительным.

4. Правильность аналитического решения можно проверить с помощью графического решения задачи.

Пример 5.3. В задаче из примера 5.1 определить ускорение ползуна В в указанном положении кривошипно-шатунного механизма, если кривошип ОА длиной 1 м равномерно вращается со скоростью 1 с^–1.

Решение.

1). Введем систему координат с началом в точке В, направив ось Вх по ВА (рис. 5.14) и определим угловую скорость шатуна АВ, используя найденные ранее скорости точек А и В : v_A = 1 м/с, v_В = м/с.

Для этого спроектируем (5.1):

v_B = v_A + v_AB (5.1´)

на оси х, y, считая все входящие в (5.1) векторы направленными в положительные стороны этих осей:

v_B cos 30˚ = v_A; (а)

v_B sin 30˚ = v_AB. (б)

Уравнение (а) повторяет содержание теоремы о проекциях скоростей двух точек плоской фигуры (5.2), а из (б) с учетом того, что v_AB = ω_AB·AB, мы найдем угловую скорость звена AB:

ω_AB = (1/AB) v_B sin 30˚ = с^–1.

Проверим правильность найденного аналитического решения графически. Для этого от произвольно выбранного центра О₁ откладываем вектор v_A и проводим через начало и конец этого вектора прямые, параллельные v_B и v_AB , до их пересечения. Найденные гипотенуза и катет векторного треугольника и будут равны v_B и v_AB соответственно. Графическое решение, как видим, свелось к построению треугольника по известной стороне и направлению двух других сторон. Величины v_B и v_AB будут положительными, поскольку векторы в многоугольнике и на чертеже совпадают по направлению. При этом

v_AB = v_A tg30˚= , ω_AB = v_AB /AB = 1/3 с^–1.

2). Для определения ускорения точки В нужно предварительно определить ускорение точки А, принадлежащей одновременно кривошипу ОА.

Поскольку ω_ОА = соnst, то полное ускорение точки А совпадает с центростремительным:

a_А = a_А^ω ω²_ОАОА = 1²·1 = 1м/с².

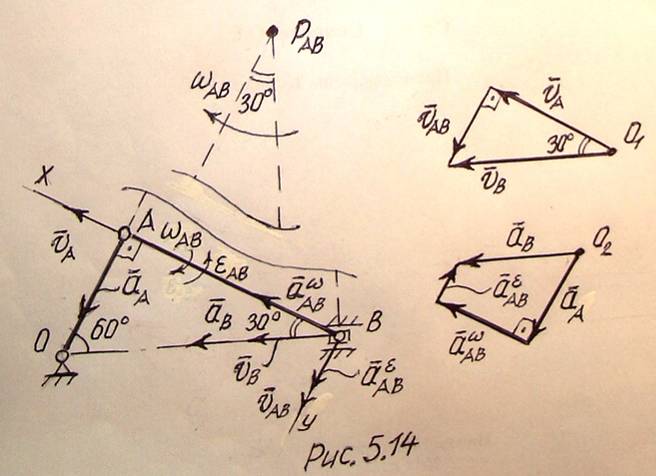
3). Для аналитического определения ускорения точки В спроектируем векторное уравнение (5.3)

a_B = a_A + a^ε_AВ + a^ω_AВ (5.3´)

на ось Bх. Учитывая, что a_A и a^ε_AВ перпендикулярны этой оси, получим:

a_B cos30 = a^ω_AВ ω² · AB = (1/3)² · = /9,

откуда

a_B = a^ω_AВ /cos30 = ( /9)/( /2) = 2/9 м/с².

Чтобы графически найти ускорения точки В построим соответствующий (5.3) векторный многоугольник. Для этого от произвольно выбранного центра О₂ последовательно откладываем векторы a_A и a^ω_AВ, а затем через начало первого и конец последнего вектора проводим прямые, параллельные a_B и a^ε_AВ до их пересечения.

Разбивая многоугольник на прямоугольник и треугольник, нетрудно определить модули векторов a_B и a^ε_AВ:

| a_В | = 2/9 м/с²; | a^ε_AВ | = | a_А | – (1/2)| a_В | = 1 – 1/9 = 8/9 м/с².

При этом проекция вектора a^ε_AВ на ось Ву : a^ε_AВ будет отрицательной, поскольку направления этих векторов на векторном многоугольнике и на чертеже противоположны.

И действительно, проектируя (5.3´) на ось Ву получим:

a_B cos60˚ = a_A + a^ε_AВ ,

откуда

a^ε_AВ = a_B cos60˚ – a_A = (1/2)(2/9) – 1 = – 8/9 м/с².

Это означает, что в данный момент времени a^ε_AВ ↑↓ v_AB и ε_AВ ↑↓ ω_AВ, то есть шатун АВ вращается замедленно.

Ответ: | a_В | = 2/9 м/с² , a_В ↑↑ v_В.

Примечания

1. Угловую скорость шатуна АВ в примере 5.3 можно было определить и с помощью МЦС этого звена, расположенного в точке P_AВ , где пересекаются перпендикуляры к векторам v_A и v_B: ω_AB = v_A / АP_AВ = 1/3 с^–1.

При этом звено АВ относительно центра P_AВ, а также точка В относительно точки А и точка А относительно точки В будут вращаться по ходу часовой стрелки.