Глава 5. Плоское движение тела

5.1. Разложении плоского движения на поступательное и вращательное

Этот вид движения ТТ заметно сложней по сравнению с поступательным и вращательным, и требует больше внимания для понимания его сути – уже потому, что не изучается в школьной программе.

Определение. Плоским, или плоскопараллельным называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных основной неподвижной плоскости.

Рассмотрим тело в виде цилиндра или призмы, скользящее своим основанием по гладкой поверхности (рис.5.1).

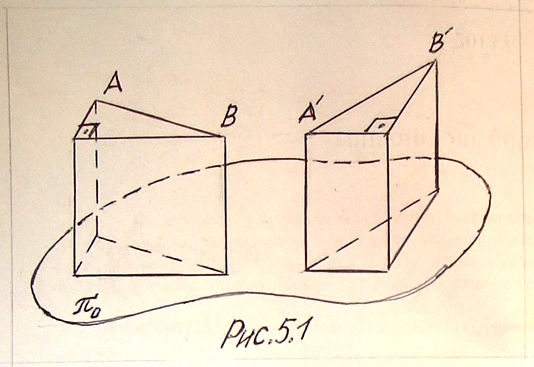
Очевидно, что это движение однозначно описывается движением любого плоского сечения π₁, параллельного неподвижной плоскости π₀, а фактически – движением любого отрезка АВ, соединяющего две фиксированные точки сечения. Поэтому в дальнейшем плоское движение тела мы будем рассматривать как движение плоской фигуры.

Вполне естественным будет вопрос, как связаны поступательное, вращательное и плоское движения? Другими словами, как поставить в соответствие множествам А, В и С, где (рис.5. 2), эти три вида движения?

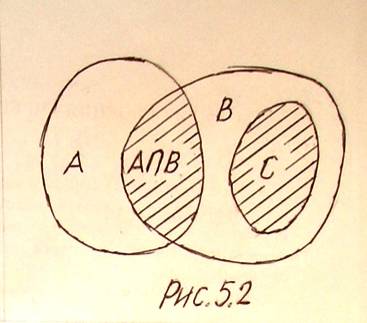
Следующая теорема дает ответ на этот вопрос.

Теорема. Плоское движение фигуры можно представить суммой двух движений: ее поступательного движения вместе с произвольно выбранной точкой – полюсом и вращательного движения фигуры вокруг этого полюса.

Доказательство. Пусть отрезок прямой, соединяющий фиксированные точки А и В такого тела, в результате его перемещения занял положение А₁В₁ (рис.5. 3).

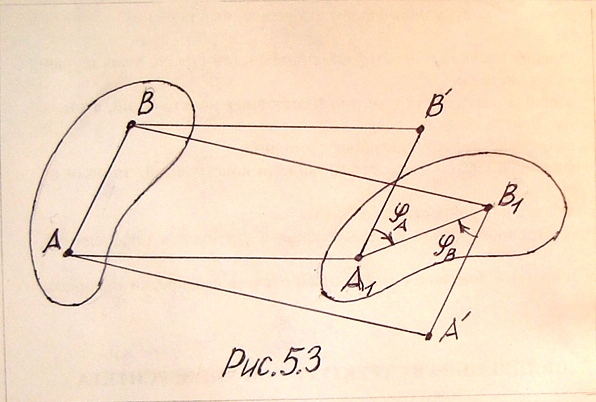
Докажем теорему, выбрав вначале в качестве полюса точку А.

Переместим тело поступательно так, чтобы отрезок АВ занял положение А₁В' || АВ, а потом повернем тело вокруг полюса А₁ на угол φ_А .

Выберем затем в качестве полюса точку В и переместим тело так, чтобы отрезок АВ занял положение А'В₁ || АВ, а потом повернем тело вокруг полюса В₁ на угол φ_В = φ_А.

Теорема доказана.

Примечания

1. Нетрудно заметить, что результат не изменится при смене последовательности движений: вначале вращательное движение, а затем – поступательное.

2. Величина углового перемещения в результате поворота тела от выбора полюса не зависит.

3. Величина поступательного перемещения зависит от выбора полюса (АА₁  АА'), и как будет показано в §3.5 полюс можно выбрать так, что величина поступательного перемещения станет равной нулю.

4. Уравнения плоского движения фигуры в плоскости xOy имеют вид:

x_A = f₁(t); y_A = f₂(t); φ = f₃(t),

где А – полюс.

5.2. Теорема о скоростях точек плоской фигуры

Теорема. Скорость любой точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости этой точки В в ее вращении относительно полюса А.

Рассмотрим плоскую фигуру с точкой А, выбранной в качестве полюса и найдем скорость любой другой ее точки В (рис.5. 4).

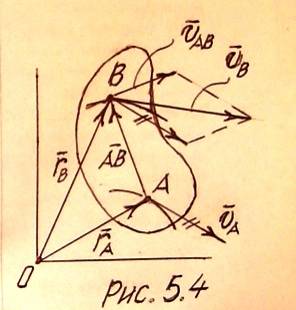
Проведем радиус-векторы точек А и В. При движении фигуры в любой момент времени будет выполняться соотношение:

r_B = r_A + AB,

где |AB| = const. Дифференцируя по времени, получим

dr_B/dt = dr_A/dt + d(AB)/dt

или

v_B = v_A + v_AB, (5.1)

где v_AB – скорость точки В в ее вращении вокруг полюса А. Напомним, что

v_AB ω  AB,

где ω – вектор угловой скорости плоской фигуры, и |v_AB| = v_AB = ω·AB.

Поскольку ω = dφ/dt, то угловая скорость плоской фигуры от выбора полюса не зависит